Существует ряд математических моделей, описывающих кривые вязкости и рео­логические кривые. Различия между этими моделями заключаются в используемых математических методах, в границах их применимости и достигаемой точности рас­четов. Обзор моделей и примеры их использования можно найти в |2,5]. В следую­щем разделе будут рассмотрены наиболее широко используемые модели для термо­пластов и эластомеров.

Степенной закон Оствальда-де Виля [6,7]

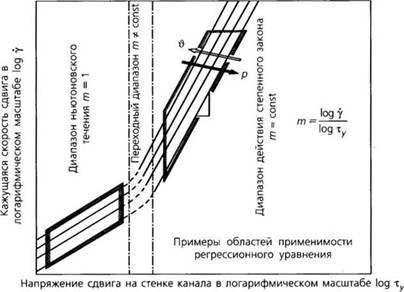
При графическом построении кривых течения для различных полимеров в двой­ных логарифмических координатах получаются кривые, состоящие из двух прибли­зительно линейных и одного переходного участка (рис. 2.3). Во многих случаях можно

Рис. 2.3. Аппроксимация реологических кривых с помощью степенного закона

рассматривать любой из двух линейных участков, и части кривой течения на линей­ных участках могут быть описаны обобщенной формулой:

У *■ ф тт. (2.5)

Уравнение (2.5) называется степенным законом Оствальда-де Виля. Параметра­ми здесь являются показатель степени степенного уравнения течения т и коэффици­ент текучести ф. Характеристикой способности материала течь и его отклонения от поведения ньютоновской жидкости является индекс течения т, который может быть описан соотношением

Algy

т 1

(2.6)

Agx

Кроме того, т является коэффициентом наклона кривой течения для прямоли­нейных участков графика в логарифмических координатах (рис. 1.3).

Для полимерных расплавов значение т лежит в диапазоне от 1 до 6. Для скоро­стей сдвига в диапазоне 10°-104 с-1, применяемых обычно при конструировании экс­трузионных головок, соответствующие значения т лежат в пределах от 2 до 4. При т= 1, ф = 1 /п, что соответствует случаю ньютоновского течения.

Так как ту = т/у, то на основании уравнения (2.5) получаем:

-I 1_1

г|= ф-[6].т1^т=ф т-ут. (2.7)

диапазоне скоростей сдвига. Ширина этого диапазона при заданной точности расче­тов зависит от кривизны графика соответствующей функции.

Если реологическую кривую описывают степенным законом в более широком диапазоне, ее необходимо разбить на участки, каждый из которых характеризуется собственным значениями ф и т, и которые должны вычисляться индивидуально для каждого участка [8].

Таким образом, набор стандартных реологических характеристик материала дол­жны содержать значения ф и т для каждого из диапазонов скоростей сдвига [9,10].

Реологическое уравнение (синус гиперболический sinA) Нрандтля-Эйринга

Эта модель была разработана Прандтлем и Эйрингом на основании наблюдений за обменными процессами между молекулами в потоке. Его математическая форму­лировка выглядит следующим образом:

/

(2.9)

Характеристические koi icrai пы материала имеют следующие размерности: [ С] = с 1,

[А] - Н/м2.

Преимущества модели Прандтля-Эйринга заключаются в том, что она дает ко­нечные значения вязкости при малых скоростях сдвига, приближающихся к нулю, а также в удобстве ее применения для анализа размерностей [14,15]. Однако ее ис­пользование для математического моделирования несколько затруднено вследствие громоздкости аргумента.

Реологическое уравнение Карро

Эта модель, популярность и значимость которой в процессе конструирования экс­трузионных головок постоянно возрастают, выражается следующим уравнением:

(2.10)

Коэффициенты этого уравнения имеют следующие размерности: [Л] = Пас, [$] = с, [С] — безразмерный параметр.

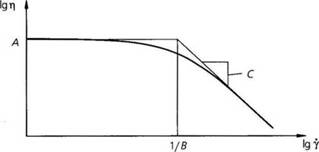
А описывает вязкость при нулевом сдвиге, В представляет собой так называемую интенсивность обратных переходов, а С— наклон кривой вязкости в диапазоне псев­допластичности при (рис. 2.4).

Основным преимуществом модели Карро является то, что она описывает факти­ческое поведение материала в значительно более широком диапазон скоростей сдви­га, нежели степенной закон. Кроме того, данная модель дает правдоподобные значе­ния вязкости при у -> 0.

Наконец, данная модель применима для получения непротиворечивых аналити­ческих решений, дающих соотношения между давлением и производительностью,

; в отечественной литературе принято обозначение shx, где х - т/А — Примеч. науч. ред.

Рис. 2.4. Аппроксимация кривой вязкости с помощью реологического уравнения Карро

как для капиллярных, так и для щелевых экструзионных головок [10-17]. Кроме того, использование этой модели позволяет проводить прикидочные расчеты даже на карманном калькуляторе. Это особенно важно в тех случаях, когда целесообразность приближенных расчетов важнее, нежели точное аналитическое решение [ 10,17]. Универсальная функция вязкости Виноградова и Малкина [18,19]

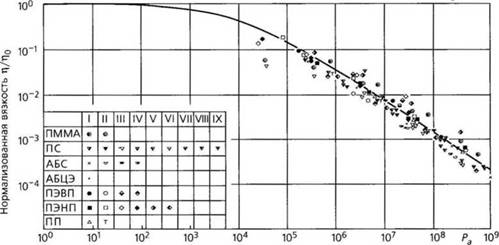
Виноградов и Малкин [18] установили, что в температурно-инвариантном пред­ставлении (см. раздел 2.1.1.3 главы 2) в диапазон рассеяния, показанный на рис. 2.5, попадают функции вязкости таких материалов, как полиэтилен, полипропилен,

Нормализованная скорость сдвига у- т|0 Рис. 2.5. Универсальная кривая вязкости по данным Виноградова и Малкина: ПММА — полиметилметакрилат; ПС — полистирол; АБС — сополимер акрилонитрила, бу­тадиена и стирола (АБС-пластик, АБС-сополимер); АБЦЭ — ацетобутиратцел - люлозный этрол; ПЭВП — полиэтилен высокой плотности; ПЭНП — полиэтилен низкой плотности; ПП — полипропилен

полистирол, полиизобутилен, поливинилбутираль, натуральный каучук, бутадиен - стирольный каучук, а также ацетилцеллюлоза.

Линию регрессии можно считать универсальной функцией вязкости, независи­мой от температуры и давления, по крайней мере, для предварительной оценки. Эта функция позволяет оценить изменение вязкости в широком диапазоне скоростей сдвига по единственной точке. При этом вязкость при нулевом сдвиге определяется методом итераций.

Графическое представление универсальной функции вязкости получено на осно­ве следующей регрессионной формулы [18]:

~ ,.ч«ч ~ :.2а ’ (2-И)

_По_

1 +/Ц ■(г у)а + А2 (г]0- у)2

где г)0 — вязкость при нулевом сдвиге или наибольшая ньютоновская вязкость, т. е. предельное значение вязкости при у —» 0; Л, — коэффициент регрессии, имеющий значение 1,386 • 10~2;/42 — коэффициент регрессии, имеющий значение 1,462 • 10-3; а — показатель степени, имеющий значение 0,355.

Значения Л, и А2 зависят от размерности вязкости и скорости сдвига. Приведен­ные выше значения справедливы для размерностей [д] - Па • с, [у] = с-1.

Преимущество универсальной функции Виноградова в том, что она содержит только один независимый параметр г|0, который легко определяется путем измере­ний. При постоянных значениях коэффициентов регрессии Av А2 и а точность вы­числения вязкости становится ограниченной. Когдау—» 0, функция вязкости Виног­радова приближается к предельному значению ri0.

Разумеется, модель Виноградова в обобщенной форме также может использо­ваться для описания функции вязкости. В этом случае/1,, Л2и а являются независи­мыми параметрами, определить которые можно методом регрессионного анализа. За счет этого возможна более точная аппроксимация, нежели аппроксимация, получен­ная с помощью параметров универсальной функции.

С другой стороны, поскольку универсальная функция определяется линией ре­грессии, проведенной через экспериментальные точки данных (рис. 2.4), вместо урав­нения (2.11) можно использовать любую другую модель, которая аппроксимирует кривую с удовлетворительной точностью.

В следующем разделе будет показано, каким образом можно использовать про­стой итерационный метод для вычисления вязкости при нулевом сдвиге на основа­нии замеренных значений скорости сдвига ур и вязкости г(( у;)). Тем не менее функция вязкости, полученная с помощью данного метода, представляет собой всего лишь оценку, которая не может заменить собой выполнение измерения вязкости во всем рассматриваемом диапазоне скоростей сдвига.

Отклонения полученной функции от реальной будут возрастать с увеличением расстояния от известной точки на кривой ( , л(У ))-

Сначала следует подставить известные значения в уравнение (2.11), которое в ре­зультате этой подстановки примет вид:

n0 = rl(y)-[l +Л101о'Тр)а + Л2(По • Ур)2а]- (2.12)

Уравнение (2.12) содержит значение г|0 в обеих частях. Точного решения для г|0 не существует, поэтому приходится искать приближенное решение, выполнив следую­щую итерационную схему:

ПО +1 = Л(у) • [1 + Aiirft - Ур)а + Л2(л” • Ур)2а]. <213>

Решая уравнение (2.13), на каждой итерации с номером и на базе оценочного зна - п П+1 Q

чения Ло получаем уточненное значение вязкости при нулевом сдвигег^ • оатем на шаге п + 1 значение Лу снова подставляется в уравнение (2.13). В результате пошаговая схема итерационного процесса выглядит следующим образом:

ШагО: приравнять г|® значение известному значению вязкости при нулевом сдвиге П(УР).

Шаг 1: вычислить новое оценочное значение для г|0, подставив значение, полу­ченное на предыдущем шаге, в уравнение (2.13).

Шаг 2: если разница между двумя оценочными значениями, полученными на двух последовательных итерациях, достаточно мала, то итерационный процесс заканчивается. Последнее полученное значение г|0 представ­ляет собой окончательный результат. Если же разница не удовлетво­ряет этому условию, вернуться к шагу 1.

Как правило, для получения результата удовлетворительной точности требуется выполнить от 5 до 10 итераций. Поскольку количество программных операций в вы­шеописанной итерационной схеме невелико, она легко программируется даже на кар­манном калькуляторе.

Модель Гершеля-Балкли [2,13,20]

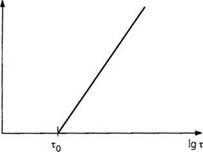
Многие полимеры, особенно эластомеры, характеризуются так называемым пре­делом текучести. Такие полимеры начинают течь, только когда напряжение сдвига превышает некоторое предельное значение, называемое пределом текучести. Жидкос­ти, для которых характерна такая модель поведения, называются бингамовскими. Кривая течения для бингамовской жидкости схематически показана на рис. 2.6, из которого видно, что скорость сдвига для бингамовской жидкости равна нулю до тех пор, пока не достигнут предел текучести т0, что означает отсутствие течения. Мате­риал начинает течь только после того, как будет превышено значение т0. Это означает, что до достижения предела текучести вязкость материала бесконечна [2].

При установившемся профиле течения бингамовской жидкости наблюдается два характерных диапазона сдвиговых течений. На первом участке сдвиговое напряже­ние т превышает значение т0, а на втором х < т0(рис. 2.7 [21]). Кроме того, из рис. 2.7 видно, что доля так называемого стержневого течения уменьшается с ростом отношения сдвигового напряжения на стенке к пределу текучести. Следовательно, модель струк­турированного течения жидкости с неразрушенным ядром потока справедлива, пока сдвиговое напряжение на стенках канала мало. Иными словами, эта модель действует

а)

ig у

Рис. 2.6. Схематичное представление кри­вой течения для бингамовской жидкости

Ь)

Рис. 2.7. Профили скоростей течения бинга­мовской жидкости в зависимости от сдвигового напряжения на стенках канала и от предела текучести [21]: а — низкое напряжение сдвига; b — высокое напряжение сдвига

( v(r)
1 г(г)^

при небольшом объемном расходе жидкости через большое поперечное сечение кана­ла экструзионной головки.

Модель Гершеля-Балкли [20] хорошо описывает течение полимера, характеризу­емого пределом текучести. Эта модель выводится на основе комбинации упрощен­ной модели Бингама (А = const для т > т0 [2]) и степенного закона. Математически эта модель формулируется следующим образом:

у=ф(т-Т0)т. (214)

При т0 = 0 уравнение (2.14) переходит в степенной закон (уравнение 2.5), а при т = 1 получается упрощенная модель Бингама.

Преобразовав уравнение (2.14), получаем следующее выражение для сдвигового напряжения:

■l. i (2-15)

т - т0 = А - у” 1-у,

‘,п

т ■

где k = ф Если

Т - Тп

П -

(2.16)

то из уравнения (2.15) при т > т0 получается соотношение, аналогичное степенному закону (уравнение 2.8):

r = k ■ у”-1.

2.1.1.1. Влияние температуры и давления на поведение потока

Кроме скорости сдвига У и напряжения сдвига т на поведение потока расплавов конкретных полимеров влияют также температура расплава Т, гидростатическое давле­ние в расплаве Phvil, молекулярная масса и ее распределение, различные добавки,
в том числе наполнители, смазки, и т. л. То есть для конкретной рецептуры полимера единственными независимыми переменными, оказывающим влияние на его течение, являются у или т, Ph d и Т.

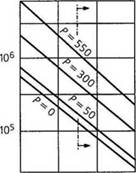
На рис. 2.8 (из [22]) показано количественное влияние температуры и давления па сдвиговую вязкость. Для наблюдаемого образца ПММА повышение давления при­мерно до 550 бар привело к десятикратному возрастанию вязкости. Для сохранения вязкости постоянной в этом случае следует повысить температуру примерно на 23 °С.

Рис. 2.9 [28] иллюстрирует влияние температуры на вязкость для различных поли­меров. Частично кристаллические полимеры, которые имеют более низкую температуру

Материал: ПММА

100 200 300 400 500 Г идростатическое давление Р, бар

190 200 210 220 0 Температура Г, “С

Рис. 2.8. Вязкость как функция температуры и гидро­статического давления (поданным [22])

25

ПЭВП	-120
ПФ	-70
пэнп	-40
пп	-10
ПА б	40
ПС	70
пвх	80
ПММА	90
АЦЭ	90

ПК

90

20 15 10

0,02

Температура стеклования Тд, 'С

Полиэтилен 8.П. Полиформальдегид (полиоксиметилен)

Полиэтилен И. П.

Полипропилен Полиамид б Полистирол Поливинилхлорид Полиметилмета - крилат

Ацетат целлюлозы, ацетилцеллюлозный этрол

Поликарбонат

Рис. 2.9. Изменение вязкости в зави­симости от температуры для различных полимеров

0,1

	Да Ад АТ~ АТ~	dig д дТ
ДПС (Гд=90 оПММА (Т	•о = 90 "С)
Диффере V (Вилья ПС Ус (тя	нцированная к мса—Ланделла = 65 “С)	ривая ВЛФ - Ферри)
пвх ПК» АЦЭ4'	• пвх пп
ПК	п?>*^ пэнггЭ*- пп пп	1 гпп | ПЭВП ПЭВП пп

0,08

0,06

0,04

50

150

250

300

Г" Г,

стеклования Tg по сравнению с аморфными полимерами, демонстрируют существен­но меньшую зависимость вязкости от температуры. Это влияние на текучесть поли­меров может быть вызвано двумя факторами [23, 24]:

• подвижностью сегментов макромолекулярной цепочки вследствие термиче­ской активации процесса (т. е. внутримолекулярной подвижностью);

• вероятностью наличия свободного объема между макромолекулярными цепоч­ками, достаточной для того, чтобы они могли меняться местами.

Влияние температуры

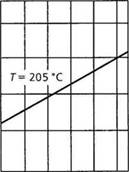
Построение кривых вязкости в двойных логарифмических координатах для иден­тичных полимерных расплавов при различных температурах (рис. 2.10) позволяет констатировать:

• во-первых, влияние температуры на вязкость более заметно проявляется при низких скоростях сдвига по сравнению с высокими скоростями сдвига, особен­но в окрестности вязкости при нулевом сдвиге;

• во-вторых, хотя кривые вязкости в зависимости от температуры смещаются, их форма остается неизменной.

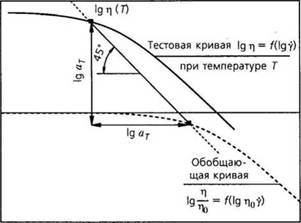
Можно показать, что практически для всех полимерных расплавов (так называе­мых термореологически простых жидкостей [25]) кривые вязкости могут быть пре­образованы в единственную обобщающую кривую, независимую от температуры. Это делается путем деления вязкости на г|0 при соответствующей температуре и путем умножения скорости сдвига на г|0 [ 13,25]. Графически это означает, что кривые сдви­гаются вдоль прямой линии с коэффициентом наклона -1, т. е. вдоль линии log(r|0(7}) направо вниз и, таким образом, преобразуются в единую кривую (рис. 2.10). Этот подход известен как принцип температурно-временной суперпозиции.

TV

104

Г

ТО С -О О й Ю3 с: со

(175*0

Обобщающая кривая V° (205 *0

ч Направ-^

lg аТ (190 "О

lg ат (190 *С)

Г = 190 ”С

ление сдвига

L

Вязкость АБЦЭ при температуре . о т = 165 *С » Т= 175 *С о Т = 190 ’С • Т= 205 *С * Т = 220 *С

ю2

10"1 1 10 ю2 ю3

Скорость сдвига у, с'1

Рис. 2.10. Кривые вязкости для ацетобутиратцеллюлозного этрола (ЛБЦЭ) при различных температурах

Принцип температурно-временной суперпозиции позволяет построить обобща­ющую кривую зависимости нормализованной вязкости от нормализованной скоро­сти сдвига. То есть для полимера можно получить единую характеристическую функ­цию вида:

(2.17)

По (7)

При этом исходную температуру можно выбирать свободно.

Для получения функции вязкости для некоторой температуры с помощью только обобщающей кривой вязкости для произвольной температуры, отличной от указан­ной, необходимо выполнить сдвиг по температуре. Значение этого сдвига заранее неизвестно. Коэффициент сдвига, необходимый для решения этой задачи, определя­ется следующим образом:

По('0 , , ПоШ

или ё07"<218)

Величина lg ат представляет собой расстояние, на которое кривая вязкости при исходной температуре должна быть сдвинута в направлении соответствующих осей координат (рис. 2.11).

«Ч* гг

_СЛ

»- 1д у -------------------------

*• igfnot) .......................

Рис. 2.11. Принцип температурно-временной суперпозиции для функции вязкости

Существует ряд формул для вычисления коэффициента температурного сдвига. Наиболее важными и заслуживающими особого упоминания являются две из них: уравнение Аррениуса и уравнение ВЛФ.

Уравнение Аррениуса вытекает из изучения чисто термоактивационного процес­са молекулярного обмена:

/1 1 4 T~T0J

. ,. в0(Т) _Е0 8 г Й^Л)"Я

(2.19)

где Е0 — энергия активации вязкого течения для заданного материала, Дж/моль; R — универсальная газовая постоянная, равная 8,314 ДжДмоль • К).

Уравнение Аррениуса особенно хорошо подходит для описания зависимости вяз­кости от температуры для частично кристаллических термопластов [10,25].

При небольших температурных сдвигах или для приближенных расчетов значе­ние «г можно определять по эмпирической формуле, не имеющей строгого физиче­ского доказательства [1,10]:

goT=-a-(T - Т0). (2.20)

Здесь а — температурный коэффициент вязкости, характерный для конкретного материала.

Еще один подход к вычислению температурного сдвига основан на теории сво­бодного объема, иными словами, на вероятности обмена молекул местами. Этот под­ход был разработан Вильямсом, Ланделлом и Ферри[ 26]. Изначальноон применялся для получения температурной зависимости релаксационных спектров, и только впо­следствии был применен и к вязкости. Соотношение, выражающее этот подход, изве­стное также как уравнение Вильямса-Ланделла-Ферри (сокращенно — уравнение ВЛФ), чаще всего имеет вид:

ц(Т) С, (Г-Г.)

<2'2,)

Это уравнение соотносит вязкость г)(7) при требуемой температуре Тс вязко­стью при стандартной температуре Ts при условии, что напряжение сдвига постоян­но. При Т:.=>Тё + 50 °С [26] (то есть, примерно на 50 °С выше температуры стеклова­ния), С, = -6,86, С2 = 101,6.

Температуры стеклования различных полимеров представлены на рис. 2.9, а до­полнительная более подробная информация приведена в работе [27]. Измерения температуры стеклования аморфных полимеров может выполняться в соответствии с процедурой А Стандарта DIN53461, которая представляет собой тест на определе­ние температуры деформационной устойчивости пластмасс под нагрузкой. В США для этой же цели используется Стандарт ANSI/ASTMD 648. Температура размягчения, полученная в результате выполнения данного теста, может быть принята равной Т [8].

Более точное описание можно получить, если Т (и, при необходимости, коэффи­циенты С, и С2, которые также можно считать зависящими от материала) определя­ются путем регрессионного анализа кривых вязкости, полученных путем измерений при различных температурах. Хотя уравнение ВЛФ по определению относится толь­ко к аморфным полимерам, для которых оно точнее уравнения Аррениуса [ 10,24,25], оно также обеспечивает приемлемую точность и применительно к частично кристал­лическим полимерам [28-31,33].

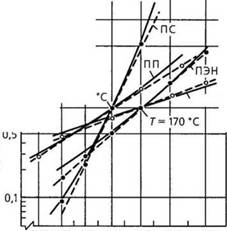
На рис. 2.12 представлены графики сравнительного анализа значений коэффици­ента сдвига ар полученных с помощью уравнения Аррениуса и уравнения ВЛФ [30]. При работе в диапазоне температур, отличающемся от исходной температуры не бо­лее чем на ±30 °С, что достаточно для большинства практических целей, оба соотно­шения дают удовлетворительные результаты.

	Стандартная температура
Полистирол (ПС)	125 "С
Полипропилен (ПП)	0 ’С
ПЭНП	10 °С
1ПЭВП	-70 ‘С

250 230 210 190 170 150 130 ‘С I | Температура Т

1,9 2,0 2,1 2,2 2,3 2,4 2,5 К10‘3 Обратное значение абсолютной температуры 1/Г

Г"Т"--т---------- 1------ 1--------- 1------- 1------- — Экспериментальные данные | ---------------- Уравнение Аррениуса Уравнение ВЛФ 11

ПЭВП

Т= 190

Рис. 2.12. Коэффициент темпера­турного сдвига для раз­личных полимеров

Существуют две основные причины, по которым уравнение ВЛФ более предпоч­тительно:

• стандартная температура Г с достаточно высокой точностью связана с извест­ной температурой стеклования Г, заданного материала (Г ж Т + 50 °К);

• влияние давления на вязкость можно легко определить при температурах, пре­вышающих стандартную температуру (более подробное объяснение приведено далее).

Если сдвиг кривой вязкости при желаемой температуре Тпо отношению к поло­жению кривой вязкости при произвольной температуре Г„ вычисляется с помощью уравнения ВЛФ, то уравнение (2.21) принимает вид:

г|(7)

лО) Л (Г.)

(2.22)

,л (т5) л ад с2 + (т0-т5) с2 + (t-ts) Здесь Г0 — исходная температура, при которой вязкость известна.

ОД-т;) сх(т - ts)

Влияние давления

Влияние давления на поведение потока может быть установлено одновременно с выводом выражения для температурной зависимости на основании уравнения ВЛФ [29]. Как выясняется, значение стандартной температуры, используемой в уравне­нии ВЛФ при давлении 1 бар и которая превышает температуру Tg примерно на 50 "С, с повышением давления увеличивается. Этот сдвиг, в свою очередь, соответ­ствует изменению температуры стеклования которое может быть непосредственно определено из диаграммы PVT(давление-объем-температура) [28,34].

Зависимость температуры стеклования от давления можно считать линейной в диапазоне давлений до 1 кбар(рис. 2.13[32]),т. е.:

О 250 500 750 1000 Гидростатическое давление phyd, бар

Т[£р) = Tg(P ” 1 бар) + С, ■ р. (2.23)

Рис. 2.13. Влияние давления на тем­пературу деформационной устойчивости и стандартную температуру соответственно

Изменения температуры стеклования ^составляютзначения порядка от 15 до 30 °С на 1 кбар давления. При давлениях больше 1 кбар температура стеклования растет гораздо медленнее.

Если для нужного полимера нет PVT-диаграммы, на основании которой можно было бы определить зависимость температуры стеклования Tg от давления, то ее мож­но приближенно оценить с помощью следующего соотношения:

Г*»?*(,бар) + (15^30). 10-з-С/Р(б1р). (2.24)

Здесь р — требуемое давление. (Обычно давление влияет на течение аморфных полимеров сильнее, чем на течение частично кристаллических полимеров.)

Таким образом, можно оценить ВЛФ-сдвиг по кривой вязкости от положения при температуре Г, и давлении рх к положению при температуре Т2 и давлении р2. При этом коэффициент сдвига агвычисляется по формуле:

Л(Т2,р2)

lgar=lg

Cl(T2-rv(p2)) Cx-(Jx-TJjpx)) C2 + (T2-TS(P2)) c2 + (rrrs(p1))-

Применение в вычислительных методах

Если точкар^у. ц^Г,)), лежащая на кривой вязкости, построенной при темпера­туре Г,, сдвигается но кривой вязкости до температуры Т2 (рис. 2.11), то справедливы следующие соотношения:

ц2 = г1 г «Г' ^2 = ^/ат,

и ат вычисляется по одному из уравнений суперпозиции. При использовании урав­нения ВЛФ значение аг может также зависеть от изменения давления от р, до р2 (р, *р2). В этом случае можно сформулировать функции вязкости таким образом, чтобы они были независимы от температуры и давления, т. е. реологическое уравне­ние Карро примет вид:

л(у. т>р)= „ . . , *,с ■ (2'26)

аТ(Т'Р)'в [1 +ат(Т, р)-А-У]С

Аналог для универсальной функции вязкости Виноградова-Малкинавэтом слу­чае записывается в виде выражения:

ат(Т, р) ■ По (2 27)

1 + А^[ат(Т, р) ■ г]0у]а + А2[ат(Т, р) ■ щ-у]2а ’

гдеЛ, = 1,386- 10~[7];Л2 = 1,462 • 10-3; а = 0,355, когда размерности [ц] = Па-с;[У] -с"1.

Поскольку функция Виноградова-Малкина фактически не зависит от материала [ 18], уравнение (2.27) представляет собой универсальную функцию вязкости, инва­риантную по отношению к материалу, температуре и давлению1.