Акустические фононы. Объемные сейсмические волны. Современная модель Земли. .Волны Рэлея и Лява. Волны в жидкостях и газах. Звук. Интенсивность звука. Иоглоение звука. Излучатели звука. Применение акустических методов. Основные характеристики звука. Закон Вебера-Фехнера. Диаграмма слуха. Акустические резо­наторы. Музыкальные инструменты. Эффект Донлера и бинауральный эффект. Ин­терференция и дифракция волн.

Тепловые колебания кристаллической решетки твердых тел. Акустические

фононы. В твердом теле ионы совершают тепловые колебания около положений равнове­сия в узлах кристаллической решетки. Поскольку они взаимодействуют друг с другом, то система ионов должна рассматриваться как совокупность связанных осцилляторов. Такие тепловые колебания ионов можно представить в виде суперпозиции стоячих звуковых волн, частоты которых w лежат в диапазоне 0 < w < wN, где wN — максимальная частота коле­баний, обусловленная дискретностью среды (см. предыдущую лекцию).

При нагревании кристалла энергия тепловых колебаний увеличивается. Естествен­но, что информацию об этих колебаниях можно получить, измеряя теплоемкость кристаллов.

Если каждый ион рассматривать как классический осциллятор, колеблющийся в трех взаимно перпендикулярных направлениях, то, в соответствии с теоремой о равно­распределении энергии по степеням свободы, он обладал бы энергией e1 = 6kT / 2, где к — постоянная Больцмана, а Т — абсолютная температура. Здесь учтено, что колеблю­щийся ион обладает средней кинетической и равной ей средней потенциальной энерги­ей kT/2 по каждой из трех степеней свободы. Поскольку энергия кристалла, состоящего из N атомов, U = Ne1 = 3NkT, то его теплоемкость при постоянном объеме равна:

хэи

cv =

= 3Nk (5.1)

ЭТ

V

и не зависит от температуры (закон Дюлонга и Пти).

Между тем, формула (5.1) согласуется с экспериментом лишь при высоких темпера­турах, а при приближении температуры к абсолютному нулю, как показывает опыт, cV ~ Т3.

Чтобы объяснить такое поведение теплоемкости, А. Эйнштейн предложил рассмат­ривать ионы как независимые осцилляторы, обладающие дискретным набором значений энергии. Ранее подобная идея была высказана М. Планком при выводе формулы для тепло­вого излучения твердого тела. Однако, А. Эйнштейну не удалось получить закон T3.

На самом деле, как уже говорилось, тепловые колебания ионов могут быть пред­ставлены как суперпозиция нормальных колебаний, или мод системы связанных ос­цилляторов. Каждая мода частоты w обладает энергией, кратной hw, где h = h /2p (h = 6,67 • 10 34 Дж/с — постоянная Планка).

Если принять во внимание, что в твердом теле возможно распространение про­дольной волны частоты w и двух поперечных волн той же частоты, имеющих два раз­
личных взаимно перпендикулярных направления смещения атомов (две различные по­ляризации), то с учетом размеров кристалла и его дискретной структуры можно подсчи­тать число мод в кристалле. Такой подсчет был впервые выполнен П. Дебаем, и поэтому эти волны получили название дебаевских.

Следует подчеркнуть, что, в отличие от классического представления, при вы­числении энергии кристалла мода представляется как квантовый объект, обладающий дискретным набором значений энергии (набором энергетических уровней)

en - nhw, (5.2)

где n — целое число.

При термодинамическом равновесии вероятность Pn возбуждения моды убы­вает по мере увеличения её энергии en (или числа n) в соответствии с распределением Больцмана: Pn ~ e-nhw/kT. При нагревании кристалла вероятность Pn растет, а значит увеличивается и запасенная кристаллом энергия. При подсчете последней Дебаем была введена характерная температура (температура Дебая) 8д с помощью равенства

£0д - hwN. (5.3)

Обычно 8д лежит в интервале (102 ^103) К. При Г >> 8д справедлив закон

Дюлонга и Пти, а при T << 8д теплоемкость cV ~ T3.

Соотношение (5.2) для энергии колебаний в моде частоты w аналогично выра­жению для энергии фотонов (квантов света). Это позволяет рассматривать моду как ква­зичастицу, называемую тепловым фононом. Введение этого нового понятия является весьма плодотворным и, с математической точки зрения, значительно облегчает анализ тепловых колебаний кристаллической решетки. Представление о фононном газе в твер­дом теле широко используется при описании таких свойств, как теплоемкость, тепло­проводность, тепловое расширение, электрическое сопротивление и др. В физике ис­пользуются и другие квазичастицы: плазмон (волна электронной плотности), магнон (вол­на перемагничивания), полярон (электрон + упругая деформация), экситон (волна поля­ризации среды). Эти квазичастицы являются модами соответствующих колебаний.

Объемные сейсмические волны. Чрезвычайно важным примером волн в уп­ругом твердом теле являются сейсмические волны, возникающие в ограниченной обла­сти пространства (очаге) размером в несколько километров и распространяющиеся на огромные расстояния под поверхностью Земли. Эти волны бывают поперечными (вол­ны сдвига) и продольными (сжатия и разрежения) и могут пронизывать всю нашу плане­ту. Это позволяет (подобно рентгеновскому анализу) исследовать внутреннее строение Земли. Этим занимается отдельная наука, называемая сейсмологией. Долгое время сей­смология, одним из основателей которой является русский физик Б. Б. Голицын, была наукой о землетрясениях и сейсмических волнах. В настоящее время сейсмология зани­мается анализом разнообразных движений в земной толще.

Скорость продольных волн приблизительно в 1,7 раза больше скорости попе­речных, поэтому эти волны регистрируются на сейсмограммах последовательно: внача­ле приходят более быстрые продольные (первичные), которые называются р-волнами, а потом поперечные (вторичные), называемые s-волнами. Кроме того, сейсмографы реги­стрируют и заметный фон, или шумы, связанные как с работой промышленных устано­вок и транспорта, так и с сейсмическими волнами (микросейсмами), генерируемыми штормами и волнением в океанах.

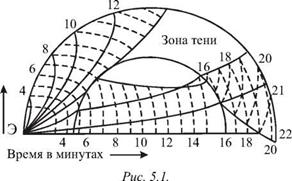
Если бы скорости р - и s-волн в Земле не менялись бы с глубиной, то волны распространялись бы по прямым линиям (прямым сейсмическим лучам). В действи­тельности скорости продольной cp и поперечной cs волн возрастают с погружением в недра Земли, за исключением небольшой зоны на глубинах 50-250 км. Поэтому сейсми­ческие лучи искривляются. В сейсмологии экспериментально определяют годограф — время t пробега сейсмических волн как функцию эпицентрального расстояния А (рас­стояния в градусах или километрах по дуге большого круга между эпицентром и прием­ником волн; 1° = 111 км). Ясно, что функция t - t(A) связана с распределением скорос­ти волны с(1) (1 — глубина), и поиск этого распределения представляет интерес при исследовании внутреннего строения Земли.

На рис. 5.1 показаны пути p-волн и указано время их распространения в недрах Земли от эпицентра Э до установленного на поверхности приемника. Прерывистые ли­нии (изохроны) указывают время прихода p-волн в различные точки земной поверхнос­ти. Из-за искривления лучей волны не попадают в обширную зону тени.

Исследование зависимости скоростей cp (1) и cs (1) от глубины позволило сде­лать вывод, что Земля разделяется на три основные части: кору, мантию и ядро. Кора отделена от мантии резкой сейсмической границей, на которой скачкообразно возраста­ют плотность p и скорости cp и cs. Эта граница была открыта в 1909 г. югославским сейсмологом Мохоровичичем и носит название границы М. Толщина лежащей выше гра­ницы М земной коры меняется от величины »10 км ( под слоем воды в океанических областях) до нескольких десятков километров в горных районах континентальных облас­тей. Ниже коры в интервале до глубин ~2900 км расположена си­ликатная оболочка, или мантия Земли. Существование ядра с плотностью, превосходящей сред­нюю плотность Земли ~ 5,5 г/см3, следует из того факта, что плот­ность земной коры (от ~2,8 г/см3 у гранитов до ~3,0 г/см3 у базаль­тов) существенно меньше этой средней плотности.

о

5-вояна____ _

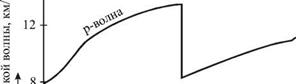
На рис. 5.2 показаны глубин­ные зависимости скоростей р - и s - волн и на базе этих

о

зависимостей про­ведено разбиение Земли на три обла­сти. Такая модель Земли называется

Ядро Внешнее

Мантия

o

ч - Внутр.

юра

классической моде-

0

2000

4000

Глубина в км

Рис. 5.2.

6000 лью Джеффриса- Центр Гутенберга. Она ос- Земли тявяпясь неизмен-

тавалась неизмен-

ной до конца 60-х годов XX века. Особенности изменения скоростей волн с глубиной связаны с изменением структуры земных пород. При переходе от коры (граниты, базаль­ты) к мантии (ультраосновные горные породы) скорости возрастают. Увеличение скоро­стей при приближении к ядру связано с наличием фазовых переходов минералов в более плотные и жесткие в механическом отношении кристаллические модификации. Паде­ние скорости р-волн при переходе из мантии в ядро есть следствие того, что внешняя часть ядра жидкая. Ядро состоит в основном из железа и небольшой примеси легких элементов. Во внешнем ядре плавное возрастание скорости cp связано с нарастанием давления к центру Земли. Во внутреннем ядре скорость p-волн не меняется, так как дав­ление к центру Земли возрастает незначительно. Естественно, что поперечные s-волны во внешней (жидкой) части ядра распространяться не могут.

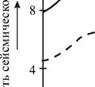
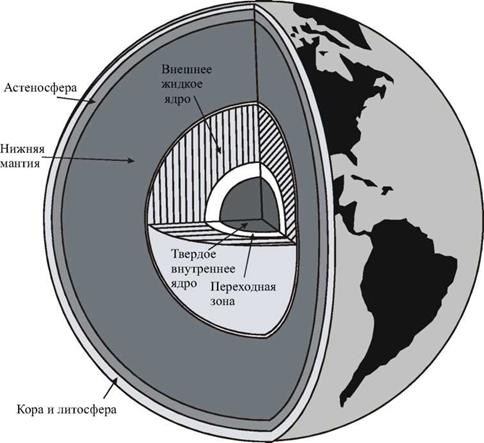
В последние годы была выявлена детальная структура мантии Земли. На рис. 5.3 показано распределение скорости cs (1) в мантии, из которого можно сделать заключе­ние о её структуре. Земная кора и верхний слой мантии до глубины 1» 70 км образуют наружную зону — литосферу, или литосферную плиту. Эта жесткая плита расколота примерно на 10 больших плит, по границам которых расположено подавляющее число очагов землетрясений. Под жесткой литосферной плитой на глубинах 70 < 1 < 250 км расположен слой повышенной текучести, называемый астеносферой. Из-за её малой вязкости (m ~ 1020 ^1021 Пуаз) литосферные плиты как бы плавают в «астеносферном океане» Земли. В астеносфере, где температура вещества близка к температуре плавле­ния, скорости волн понижены. Начиная с 1 » 250 км скорости возрастают из-за увели­чения давления. При 1» 400 км возрастание скорости есть результат фазовых перехо­дов (минералы оливины переходят в шпинелевую модификацию), а на глубинах 400 < 1 < 650 км скорость возрастает из-за роста давления. На глубинах 650 < 1 < 700 км расположена вторая зона фазовых переходов, однако остается открытым вопрос о том, какие конкретно переходы ответственны за быстрый рост скорости.

На рис. 5.4 изображен разрез Земли, построенный в соответствии с современ­ными сейсмическими данными.

Рис. 5.3.

При распространении объемной сейсмической волны в трехмерном случае ам­плитуда уменьшается с расстоянием г, пройденным волной от точечного источника. Урав­нение такой волны, называемой сферической, имеет вид:

■	/	■
	r
w	t----
	c
-	V /	-

/ , ~0 - ar • s(r, t) -— e sin r

(5.4)

Из этого уравнения видно, что амплитуда волны убывает, во-первых, из-за ее геометри­ческого расхождения во все стороны от эпицентра; это убывание происходит обратно пропорционально пройденному волной расстоянию г. Во-вторых, амплитуда волны убы­вает из-за перехода части энергии волны в тепло вследствие неидеальной упругости зем­ных недр. Это ослабление характеризуется коэффициентом затухания a. Коэффициент a пропорционален частоте сейсмической волны, поэтому короткие волны затухают быстрее длинных. Расчет показывает, что для коэффициентов затухания s - и p-волн мо­гут быть записаны соотношения

as (км-1) — 110-3v (Гц); ap (км-1) ~0,25 10-3v (Гц)

Частоты объемных сейсмических волн лежат в инфразвуковом диапазоне 0,1 Гц <v <10 Гц. Следовательно, для волн с частотой v ~ 1 Гц уменьшение амплитуды в е раз у поперечной волны происходит на пути —1000 км, а у продольной волны — на пути ~ 4000 км.

Помимо бегущих волн, в объеме Земли могут наблюдаться и стоячие волны, когда вся Земля колеблется, как целое, с различными частотами, соответствующими различным модам колебаний. Конфигурации этих мод относятся к двум основным ти­пам: сфероидальные колебания (наибольший период —55 мин., частота — 3 • 10-4 Гц) и торсионные (крутильные) колебания (наибольший период —44 мин., частота — 3,8 • 10-4 Гц). В настоящее время спектр этих колебаний насчитывает несколько ты­сяч экспериментально обнаруженных частот.

Поверхностные сейсмические волны. Наряду с объемными, по Земле могут рас­пространятся и поверхностные волны. Эти волны бывают двух типов и называются волнами Рэлея и Лява. Они были теоретически предсказаны Дж. Рэлеем в 1855 г. и Лявом в 1911 г. В Рэлеевской волне частицы грунта смещаются в вертикальной плоскости, ориентированной вдоль направления распространения волн, а траектории их движения представляют собой эллипсы (см. далее гравитационные волны на поверхности жидкости). В волне Лява частицы движутся в горизонтальной плоскости поперек направления распространения волны.

Длины поверхностных волн 1, возбуждаемых при землетрясении, лежат в ин­тервале от десятков до многих сотен километров. В поверхностных волнах амплитуда убывает с глубиной, и на глубине 1 >1 колебания мантии малы. Поэтому с помощью таких волн можно исследовать лишь наружные слои Земли.

Из-за двумерного распространения амплитуда поверхностных волн убывает мед­леннее (обратно пропорционально 4т ), чем у объемных волн. Поэтому такие волны могут по несколько раз обегать вокруг земного шара. Скорость поверхностных волн зависит от частоты, т. е. они обладают дисперсией.

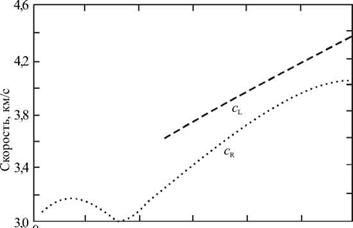
На рисун­ке 5.5 показаны за­висимости группо­вых скоростей волн Рэлея cR и Лява cL от периода колеба­ния волны. Легко ви­деть, что волны Лява распространяются быстрее волн Рэлея.

20 40 Период, с Рис. 5.5.

Отметим, что на рис. 5.5 показаны cR и cL лишь для волн, амплитуды ко­торых определенным образом убывают с глубиной. Возможны поверхностные вол­ны и с другими распределениями амплитуд по глубине.

Сейсмические волны можно вызвать при помощи взрыва. Небольшие взрывы используются в инженерной сейсмологии для проведения разведки полезных ископае­мых (нефти, руды, газа и т. д.). Подземные ядерные взрывы создают интенсивные вол­ны, которые можно регистрировать на любых расстояниях. Это дает возможность на­дежно проводить контроль над подземными ядерными испытаниями.

Волны в жидкостях и газах. В жидкостях и газах возможны лишь деформации сжатия и растяжения, поэтому в них могут распространятся только продольные волны. Хотя мы ранее и рассчитывали скорость распространения возмущений в газе, тем не менее вычислим скорость распространения продольных волн с использованием волно­вого уравнения. Последнее может быть получено из (4.74), в котором о n следует заме­нить величиной -5p = p - p, где р — давление в волне, p — равновесное давление в среде, 5р — возмущение давления. Тогда мы можем записать

Э2 s

dm —2- = [-5p( x + dx, t) + 5p(x, t)]S Эг2

(5.5)

Чтобы из (5.5) получить волновое уравнение, необходимо знать материальное уравнение среды

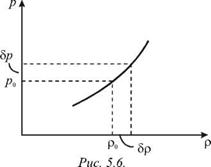
Р = ,Р(Р). (5.6)

Качественно эта зависимость изобра­жена на рис. 5.6. При очень малых возмущени­ях плотности |5р| << р0 и давления |5р| << p из (5.6) получаем:

/ dp 4 Vdp7 P0

SP -

(5.7)

•5p - c 2§p,

где введено обозначение

(5.8)

xdp 4 Vd^ P0

С учетом (4.69) и (4.72) возмущения плотности Sp в (5.7) связаны со смещени­ем s соотношением:

Э? Эх

(5.9)

SP--eP0 --p0

Следовательно, (5.7) примет вид:

S „2 Э? Ф --P 0 c T-. Эх

т Э?

(5.10)

Подставляя (5.10) в (5.5), записывая dm - P0Sdx и переходя к пределу при dx ® 0 , получим волновое уравнение

2

Э 2 s

Э 2 s

(5.11)

Эt2 Эх2

из которого сразу видно, что скорость волны задается выражением (5.8) и не зависит от частоты (дисперсия отсутствует). Естественно, что с такой скоростью распространяют­ся волны с длиной волны 1, превосходящей длину свободного пробега молекул в газе или межатомные расстояния в жидкостях 1. В этом случае жидкость и газ могут рас­сматриваться как сплошные среды. Для волн высоких частот, когда 1 — 1, возникает дисперсия, а волны с длиной 1 < 1 распространяться вообще не могут.

Упругие волны в жидкостях и газах, как, впрочем, и в твердых телах, называются акустическими, а раздел физики, который их изучает — акустикой. Частоты этих волн ле­жат в диапазоне от долей герца (инфразвук) до 1013 Гц (гиперзвук). Этим частотам соответ­ствуют длины волн 1 от десятков километров до нескольких ангстрем. Значения скоростей (фазовых и групповых) для разных сред лежат в диапазоне от долей до десятков км/с.

Для воздуха материальное уравнение (5.6) является уравнением адиабаты и в акустике обычно записывается в виде (см. также предыдущие лекции):

/ Y

(5.12)

p - p 0

Р_

P0

где g - / cV — показатель адиабаты.

с -,|т— - ,/Г P0 V m

где m — молярная масса газа.

Тогда из (5.8) скорость волны (в акустике употребляют термин «скорость зву­ка») в газе получается равной

Скорость звука зависит, таким образом, от рода газа и по порядку величины совпадает со средней скоростью теплового движения молекул.

Для жидкости материальным уравнением является полуэмпирическое уравнение Тета:

где рвн — характерное внутреннее давление, обусловленное межмолекулярным взаи­модействием (оно составляет для большинства жидкостей без пузырьков и различных включений несколько тысяч атмосфер). Параметр Г имеет порядок нескольких единиц (например, для воды Г » 7).

В таблице приведены значения скорости звука, измеренные в некоторых газах (при температуре t = 0°C) и жидкостях.

Газы	Скорость звука, м/с	Жидкости	Скорость звука, м/с
Водород	1265	Вода (г = 20°C)	1490
Г елий	965	Этил. спирт (г = 20°C)	1180
Азот	334	Водород (г = -252°C)	1127
Воздух	331	Кислород (г = -183°C)	911
Кислород	316	Азот (г = -196°C)	867
Углекислота	216	Гелий (г = -269°C)	180

Энергия, переносимая звуковой волной. Интенсивность звука задается формулой (4.65)

1 = 2 cp0W2s0 (5.15)

и пропорциональна квадрату частоты. Поэтому при переходе в область высоких частот об­легчается задача получения больших интенсивностей, необходимых, например, для наблю­дения нелинейных эффектов (см. следующую лекцию). В зависимости от решаемой задачи в акустике используются волны с интенсивностью от 10-8 Вт/см2 до 106 Вт/см2.

Для практических целей интенсивность I выражают через возмущение давле­ния dp, которое называют также «звуковым давлением». Наиболее просто такую зави­симость можно получить из (5.15) при учете, что амплитуда скорости колебаний частиц v0 = ws0 . С другой стороны, в соответствии с акустическим законом Ома (формула (3.53) в лекциях по механике сплошных сред) эта скорость равна

(dP)0 (516)

v0 = , (5.16)

P0c

где (dp)0 — амплитуда колебаний возмущений давления dp. Поэтому

I =1 (dp)° . (5.17)

2 P0c

Выполним некоторые простые оценки.

1. Вблизи струи газа, вытекающей из сопла реактивного двигателя самолета, амплитуда колебаний звукового давления (5p)0 = 300 Па (вспомним, что р0 = 105 Па и (5p)0 << p. Такое давление находится на пороге болевого ощущения (см. далее). По­скольку акустическое волновое сопротивление воздуха z = р0 с = 41 см-2-с-1, то v0 = 73 см/с. Если принять, что частота V = 103 Гц (хотя из турбины исходит многочас­тотный шум), то амплитуда смещения s0 = v0 / 2pv = 0,01 см. Таким образом, смеще­

2. Звуки на пределе слышимости на частоте V = 103 Гц (ухо человека весьма

ние частиц воздуха даже при таком сильном звуке оказывается малым

человека

-1-5

чувствительно к этой частоте) имеют амплитуду звукового давления (5p)0 = 2 -10 Па, а смещение частиц воздуха s0 = 0,8 -10-9 см. Уместно заметить, что современные мето­ды измерения смещений в принципе дают возможность зарегистрировать колебания с

1 л —16

амплитудой ^0 ~10 см.

3. В ультразвуковых волнах с частотами порядка нескольких мегагерц интен­сивности могут достигать нескольких сотен Вт/см2, а с использованием фокусирующих устройств — даже более десятка кВт/см2. Это приводит к появлению огромных ускоре­ний частиц среды, в которой распространяется ультразвуковая волна. Например, при распространении в воде волны с частотой V = 106 Гц и интенсивностью I = 100 Вт/см2 амплитуда ускорения а0 = w2s0, согласно (5.15), получается равной

a0 = W = 6,3 -108 см-с 2 ~ 105 g, (5.18)

V сР0

что на пять порядков превосходит ускорение свободного падения g. Учет появления таких громадных ускорений особенно важен в биологических исследованиях с при­менением ультразвука.

Поглощение звука. Наличие вязкости и теплопроводности среды приводит к потере энергии звуковой волны, и эта энергия расходуется на нагревание среды. Волна давления 5p(r, t), а также волны смещения s(r, t) и скорости v(r, t) = / 5t по мере

распространения затухают. Здесь r — радиус-вектор, задающий положение точки в трех­мерном пространстве, в которой фиксируются возмущения давления, смещение частиц и их скорость. В случае гармонической волны, распространяющейся по одному направ­лению (вдоль оси Ox), возмущения давления записываются в виде

Ф(Xt) = (dP)0е_°“ sin fflft — - , (5.19)

где a — коэффициент затухания. Это уравнение характеризует плоскую волну (возму­щение 5р в плоскости x = const одинаково). В этом случае отсутствует геометрическое расхождение волны. Амплитуда этой волны (dp)0 e-ax экспоненциально убывает с прой­денным расстоянием. В соответствии с (5.17) интенсивность волны равна

(5.20)

02

где I0 =

1 (dp )0-------------- начальная интенсивность волны. Если пренебречь потерями, связанны-

2 Р0c

ми с теплопроводностью, то коэффициент a, согласно гидродинамике, оказывается равным

(5.21)

2

где m — вязкость жидкости или газа. Важно отметить, что a ~ w. Этим объясняется

тот факт, что резкий звук выстрела или щелчка кнута, в спектре которого присутствует широкий набор частот, по мере распространения трансформируется в более мягкий, поскольку в спектре остаются преимущественно низкие частоты. Заметим, что погло­щение звука в воде существенно меньше, чем в воздухе, а в твердых телах еще меньше, чем в воде. Очень низким поглощением звука отличаются такие кристаллы, как сапфир, топаз, берилл, ниобат лития и другие.

В заключение отметим, что поглощение звука является главным препятствием, ограничивающим применение многих материалов на высоких частотах.

Излучатели звука. Применяемые в акустике излучатели упругих волн можно подразделить на две большие группы.

К первой относятся излучатели-генераторы; колебания в них возбуждаются из - за наличия препятствия на пути постоянного потока газа или жидкости (сирены, свист­ки, генераторы Гартмана). Такие генераторы применяются в основном в диапазоне час­тот до 30 + 40 кГц. Они отличаются высоким коэффициентом преобразования кинети­ческой энергии струи в акустическую (до 50%), простотой конструкции и эксплуатации, дешевизной. Интенсивность звука в непосредственной близости от излучателя может достигать 10 Вт/см2. К недостаткам этих излучателей относятся широкий спектр излу­чаемых частот, нестабильность излучаемой мощности, невозможность получения зву­ковых колебаний заданной формы.

Вторую группу излучателей составляют электроакустические преобразователи. Свое название они получили оттого, что преобразуют электрические колебания в механи­ческие колебания какого-либо твердого тела, которое и излучает в окружающую среду аку­стические волны. Наиболее распространенные электроакустические преобразователи, та­кие, как электродинамические излучатели, магнитострикционные и пьезоэлектрические преобразователи, представляют собой линейные устройства, благодаря чему они возбужда­ют акустическую волну той же формы, что и электрический сигнал. Кроме того, эти устрой­ства обратимы, то есть могут работать и как излучатели, и как приемники звука.

В диапазоне слышимых частот широкое распространение получили электроди­намические излучатели, принцип действия которых основан на взаимодействии пере­
менного электрического тока с магнитным полем (телефоны, громкоговорители). В маг - нитострикционных преобразователях используется эффект магнитострикции — дефор­мации твердого тела в магнитном поле.

В ультразвуковом и гиперзвуковом диапазонах (до 1010 Гц) наиболее широко применяются пьезоэлектрические преобразователи, принцип действия которых основан на обратном пьезоэффекте — деформации тела под действием электрического поля.

Рис. 5.7.

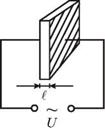
На рис. 5.7 схематично показан простейший преобразова­тель, основу которого составляет пьезопластинка, вырезанная спе­циальным образом из монокристалла кварца, ниобата лития (LiNbO3) или другого пьезоматериала. К противоположным повер­хностям пластинки (обычно металлизированным или покрытым металлическими электродами) прикладывается переменное напря­жение U с частотой V. Толщина пластинки 1 будет при этом пери­одически изменяться с той же частотой, причем это изменение не превосходит нескольких микрон. Вибрирующие поверхности пластинки приводят в дви­жение соприкасающийся с ними воздух. Наибольшая амплитуда колебаний будет при резонансе, когда на толщине 1 укладывается нечетное число полуволн:

l n

1 = n-^; n = 1, 3, 5 ... 2

(5.22)

Отметим, что при четном n на электродах возникли бы электрические заряды одного знака, что невозможно. Резонансные частоты получаются равными

V n =^г = “. (5.23)

n 1n 21

Например, для пьезокварца при скорости продольных волн c = 5700 м/с и тол­щине пластинки 1 = 1 мм резонансные частоты равны

V n = n • 2850 кГц. (5.24)

Наибольшую амплитуду колебаний имеет волна основной частоты (n = 1), по­этому пьезоизлучатели применяются, как правило, на основной частоте.

На частотах до нескольких мегагерц широкое распространение получили пре­образователи из пьезокерамики. Пьезокерамика представляет собой поликристалличес - кий сегнетоэлектрический материал (твердые растворы на основе BaTiO3-CaTiO3, PbTiO3-PbZnO3 и другие), обладающий после поляризации в электрическом поле ус­тойчивыми и сильными пьезоэлектрическими свойствами. Из пьезокерамики можно изготавливать излучатели самой разной формы (в виде пластин, стержней, колец и так далее). С помощью преобразователей сферической или цилиндрической формы получа­ют сфокусированный ультразвуковой пучок, в фокусе которого интенсивность звука до­стигает 105 -И06 Вт/см2.

На частотах порядка десятков и сотен мегагерц толщина 1 становится настолько ма­лой, что изготовить преобразователь можно лишь в жестком соединении со звукопроводом — массивным куском звукопроводящего материала. В этом случае на хорошо отполированную по­

верхность звукопровода напыляется металлическая пленка (один электрод), к которой привари­вается толстая (порядка 1 мм) пластинка пьезоэлектрика. Затем эта пластинка сошлифовывается до нужной толщины 1, после чего на неё наносится второй электрод.

На частотах порядка 1 ГГц толщина пьезопреобразователя составляет 1 ~ 1 мкм. Изготовление таких преобразователей представляет серьезную технологическую про­блему. В этом частотном диапазоне применяются пленочные преобразователи, получае­мые напылением на торец звукопровода пьезоэлектрических пленок из таких материа­лов, как CdS, ZnS, ZnO и другие. Современные технологии позволяют создавать преоб­разователи с коэффициентом преобразования электрической энергии в акустическую до 90% и мощностью волны, достигающей нескольких ватт.

Применение акустических методов. Для современного уровня развития акус­тики характерно чрезвычайно широкое применение акустических методов для решения разнообразных задач не только в физике, но также и в информационной и измеритель­ной технике, промышленности, медицине, биологии, военном деле и т. д.

Первое (в порядке исторического становления) важное прикладное направле­ние в акустике связано с получением при помощи акустических волн информации о свойствах и строении веществ, о происходящих в них процессах. Применяемые в этих случаях методы основаны на измерении скорости распространения и коэффициента поглощения ультразвука на разных частотах (104 +105 Гц в газах и 105 +1010 Гц в жид­костях и твердых телах). Такие исследования позволяют получать информацию об уп­ругих и прочностных характеристиках материалов, о степени их чистоты и наличии примесей, о размерах неоднородностей, вызывающих рассеяние и поглощение волн, и т. д. Большая группа методов базируется на эффектах отражения и рассеяния упругих волн на границе между различными средами, что позволяет обнаруживать присутствие инородных тел и их местоположение. Эти методы лежат в основе таких направлений, как гидролокация, неразрушающий контроль изделий и материалов, медицинская диаг­ностика. Применение акустической локации в гидроакустике имеет исключительное значение, поскольку звуковые волны являются единственным видом волн, распростра­няющихся на большие расстояния в естественной водной среде. Как разновидность де­фектоскопии, широко применяемой в промышленности, можно рассматривать ультра­звуковую диагностику в медицине. Даже при небольшом различии в плотности биоло­гических тканей происходит отражение ультразвука на их границах. Поэтому ультра­звуковая диагностика позволяет выявлять образования, не обнаруживаемые с помощью рентгеновских лучей. В такой диагностике используются частоты ультразвука порядка 107 Гц; интенсивность звука при этом не превышает 0,5 мВт/см2, что считается вполне безопасным для организма. В настоящее время развитие дефектоскопии привело к со­зданию акустической томографии. В этом методе с помощью набора приемников ульт­развука или одного сканирующего приемника регистрируются упругие волны, рассеи-

ваемые в разных направлениях, а затем с использованием компьютерной обработки сигналов на экране дисплея формируется объемное изображение внутренней структу­ры исследуемого объекта.

Другим важным прикладным направлением акустики является активное воздей­ствие ультразвуком на вещество. Такое воздействие широко используется в промышленной технологии для поверхностной обработки деталей, сварки, интенсификации химических процессов и т. д. В жидкостях основную роль при таком воздействии играет кавитация — образование в интенсивной звуковой волне пульсирующих пузырьков. Схлопывание пу­зырьков сопровождается мощным гидродинамическим возмущением и сильным локаль­ным разогревом вещества, в результате чего разрушается поверхность твердого тела, нахо­дящегося в области кавитации. Применение ультразвука для воздействия на живой орга­низм в медицине основывается на эффектах, возникающих в биологических тканях при прохождении через них акустических волн. При умеренной интенсивности звука (до 1 Вт/см2) колебания частиц среды вызывают микромассаж тканей, а поглощение звука — локальный разогрев, что применяется в ультразвуковой терапии. При больших интенсивно­стях сильное нагревание и кавитация вызывают разрушение тканей. Для хирургических операций используется сфокусированный ультразвуковой пучок, который позволяет произ­водить локальные разрушения в глубинных структурах (например, мозга или почки) без повреждения окружающих тканей. В хирургии применяется ультразвук с частотами 0,5 + 5 МГц, интенсивность которого в фокусе достигает 103 Вт/см2.

Основные характеристики звука. Упругие волны в воздухе, имеющие часто­ты в пределах от 20 Гц до 20 кГц, вызывают у человека ощущение звука. В узком смысле упругие волны в любой среде, имеющие частоту в этом интервале, называются слыши­мыми звуковыми волнами, или просто звуком. Волны с частотами V < 20 Гц называют­ся инфразвуком, а с частотами V > 20 кГц — ультразвуком. Инфразвук и ультразвук че­ловеческим ухом не воспринимаются.

В действительности, самые низкие и самые высокие частоты интервала слыши­мых звуков доступны, как правило, лишь очень молодым людям. С возрастом этот ин­тервал сужается, причем мужчины начинают утрачивать чувствительность к высоким частотам раньше, чем женщины. После 50 лет люди чаще всего утрачивают способ­ность к восприятию звуков с частотами V > 12 кГц.

.ОС

f

Звуки различаются по высоте, тембру и громкости.

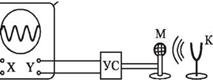
Всякий реальный звук, как прави­ло, представляет собой не простое гармони­ческое колебание, а является наложением ко­лебаний с определенным набором частот. Чтобы убедиться в этом, подключим микро­фон М через усилитель УС ко входу Y ос­

циллографа ОС (рис. 5.8) и будем регистрировать осциллограммы различных источни­ков звука. Наиболее близким к гармоническому является звук камертона К — осциллог­рамма по своему виду очень близка к синусоиде.

Из произносимых звуков более всего походят на гармонические гласные звуки. Однако уже здесь заметно отличие осциллограммы от синусоиды, что указывает на слож­ный состав гласных звуков. Гораздо более сложный вид характерен для осциллограмм согласных звуков. Принципиально возможно, используя набор резонаторов (см. ниже) или компьютерную обработку осциллограмм, произвести гармонический анализ звука, то есть установить тот набор частот, который присутствует в данном звуке. Измеряя ин­тенсивность каждой из гармоник, можно получить акустический спектр.

Рис. 5.9.

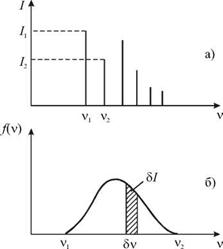
Если в результате такого анализа ока­жется, что звук состоит из колебаний с диск­ретными частотами Vj, V2, V3 и так далее, то спектр называется линейчатым. На рис. 5.9а показан пример такого спектра, где по оси ординат отложены интенсивности I простых (гармонических) звуков.

Может быть и другая ситуация, ког­да в звуке присутствуют колебания всех час­тот в некотором интервале V1 < V <V2. Та­кой спектр, изображенный на рис. 5.9б, на­зывается сплошным. По оси ординат здесь отложена так называемая спектральная плот­ность интенсивности звука f (v) = dI / dV. В этом случае можно говорить об интенсивно­сти dI = f (v)dv звука, занимающего узкий частотный интервал dv. Эта интенсивность численно равна заштрихованной на рисунке площади. Естественно, что полная интен­сивность I сложного звука со сплошным спектром будет равна площади под кривой f (v) . Сплошным спектром обычно обладают шумы.

Колебания с линейчатым спектром вызывают ощущение звука с более или менее определенной высотой. Такой звук называется тональным. Высота тонального звука опре­деляется основной (наименьшей) частотой V1. Колебания с частотами V2, V3 и так далее называются обертонами. Соотношения интенсивностей основного тона Ij и обертонов 12, Iз, ... определяют тембр звука, придают ему определенную окраску. Фазы гармоник на тембр звука не влияют. В отсутствие обертонов тональный звук называют чистым тоном. Камертоны дают чистый тон и используются при настройке музыкальных инструментов.

Из каждого музыкального инструмента извлекают звуки с характерным набо­ром гармоник. Это позволяет на слух различать звуки одного тона (с одинаковой основ­ной частотой Vj), извлекаемые из флейты, трубы, фортепьяно и др. На рис. 5.10 показа-

а)

В)

ны осциллограммы для тональных звуков с частотой Vj = 440 Гц (нота «ля» первой октавы) флейты (а), голоса (б) и трубы (в). Все осциллограммы имеют одинаковый пе­риод повторения T = 1/440 с, однако сильно разнятся своим видом. Это указывает на то, что основные частоты V1 = 1/T у всех звуков совпадают, однако звуки отличаются своим спектральным составом.

На рис. 5.11 изображена клавиатура рояля с указанием основных частот клавиш, а также приближенные диапазоны основных частот для других инструментов и голосов.

Закон Вебера-Фехнера. Диаграмма слуха. Определение громкости звука ос­новано на психофизическом законе, установленном в 1846 году Э.-Г Вебером, который заложил основы «психометрии», т. е. количественных измерений ощущений. Поскольку ощущение является субъективным процессом, то абсолютные измерения силы ощуще­ний невозможны, и Вебер перенес проблему в область измерения относительных вели­чин и искал минимальные различия в ощущениях, которые можно зафиксировать.

Суть закона Вебера заключается в том, что минимальное изменение интенсив­ности звука ДІ, которое различает человеческое ухо, не зависит от интенсивности I слы­шимого звука и составляет приблизительно 10% от ее величины:

— = 10-1. (5.25)

I

Помимо слуховых ощущений, Вебер изучал также осязание и зрение и установил, что для осязания минимальное различие в ощущении тяжести груза не зависит от величи­ны этого груза и составляет ~1/30, а для зрения минимальная воспринимаемая разница в интенсивности света также не зависит от величины интенсивности и составляет ~1/100.

Исходя из закона Вебера, можно построить шкалу уровня ощущения звука, или шкалу громкости Р, записав следующее соотношение:

у = Adp, (5.26)

где dp — прирост громкости, обусловленный приростом интенсивности, А — коэффи­циент, определяющий масштаб шкалы. Интегрируя (5.26), получаем:

ln — = Ap. (5.27)

1 пор

Для того, чтобы вызвать звуковое ощущение, волна должна обладать некоторой минимальной интенсивностью 1пор и соответственно, некоторым минимальным звуко­вым давлением 5рпор, которое называется порогом слышимости. Естественно, что при I = 1пор громкость Р = 0. Следовательно,

v, Гц 29,14 34,65 38,89 46,25 51,91 58,27 69,30 77,78 92,50 103,83 116,54 138.6 155.6 185.0 207.7 233.1 277.2 311.2 370.0 415.3 466.2 554.4 622.3 740.0 830,6 932.3 1108,7 1244,5 1480 1661 1865 2218 2489 2960 3322 3729

Рояль

Инструменты Струнные Деревянные Медные духовые духовые

v, Гц

27,50

30,87

32.70

36.71 41,20 43,65

49.00

55.0 61,74

65.41

73.42 82,41 87,31

98.0 110,00 123,47

130.81 146,83

164.81 174,61

196.00

220.0 246,94

261.63 293,66

329.63 349,23

392.00

-Яя 440,00

1-й октавы, по „„ 493,88

523.25 587,33

659.26 698,46 783,99

880.0 987,77

1046.50 1174,66

1318.51 1396,91 1567,98

1760.0 1975,53

2093.0 2349,32 2637,02 2793,83 3135,96

3520.0 3951,07

4186.01

Голос

а

а

I

н

£

Р = ^ In j-. (5.28)

л 1 пор

Если выбрать A = ln10 » 2,301, то (5.28) перепишется в виде

b = lg. (5.29)

пор

Это соотношение называется законом Вебера-Фехнера и отражает тот факт, что чувствительность уха человека к звуку меняется, как логарифм интенсивности зву­ка. Аналогичные (5.29) соотношения были установлены Э.-Г. Вебером и Г.-Т. Фехне - ром и для других ощущений, даваемых органами чувств человека, — осязания и зрения (Фехнеру принадлежит большое количество работ по «психофизике», которую он опре­делял, как «точную науку о функциональных зависимостях между телом и душой, об­щее — между материальным и духовным, физическим и психическим миром»).

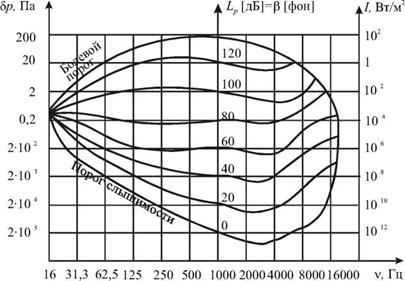
На рис. 5.12 изображена «диаграмма слуха», на которой показаны области частот и звуковых давлений, а также уровни интенсивности звуков, воспринимаемых человеческим ухом. Нормальное ухо слышит только те звуки, которые лежат внутри этой области. Ниж­няя граница области характеризует зависимость порога слышимости от частоты, а верх­няя — порог болевого ощущения, когда волна перестает восприниматься как звук, вызывая в ухе ощущение боли и давления. Отметим, что человеческое ухо является уникальным приемником акустических волн, воспринимающим звуки, различающиеся по интенсивно­сти на 12-15 порядков в области частот около 1 кГц, где диаграмма слуха имеет наиболь­шее вертикальное сечение. Из диаграммы видно, что при одинаковом звуковом давлении и одинаковой интенсивности звуки различной частоты могут восприниматься, как звуки раз­ной громкости b. Поэтому в акустике, помимо субъективной величины — громкости звука b, оцениваемой на слух, используются и объективные характеристики звука, которые мо­гут быть непосредственно измерены, уровень звукового давления и равный ему уро-

вень интенсивности. Поскольку согласно (5.17) интенсивность пропорциональна квадрату звукового давления, обе эти характеристики определяются формулой:

dp I

- 21g— - lg - . (5.30)

Чг пор пор

В принципе, — величина безразмерная, но для численного значения логариф­ма используют название «бел» (в честь изобретателя телефона Г. Белла). На практике обыч­но используют в 10 раз меньшую единицу — «децибел», так что (5.30) принимает вид:

[дБ] - 20lg - 101g. (5.30а)

пор пор

В определении L- принято использовать стандартный порог слышимости 5рпор - 2 -10 5 Па, а соответствующее ему значение минимальной интенсивности Iпор зависит, согласно (5.17), от среды, в которой распространяется звук, и для воздуха при нормальных условиях составляет 1пор - 10-12 Вт/м2.

Для громкости звука b используют единицу под названием «фон». Громкость тона в фонах для любой частоты равна уровню звукового давления в децибелах для тона с частотой V - 1 кГц, воспринимаемого как звук той же громкости.

На рис. 5.12 изображены также кривые для уровней равной громкости при раз­личных уровнях звукового давления и интенсивности, из которых видно, что при V - 1 кГц b - , а для других слышимых ухом частот b и могут заметно отличаться.

Акустические резонаторы. В ряде случаев возникает необходимость выделе­ния гармонических составляющих из сложных звуковых колебаний. С такой задачей приходится сталкиваться при упомянутом выше спектральном анализе сложных зву­ков, при создании узкополосных приемников звука, чувствительных к определенной частоте, музыкальных инструментов и др. Для таких целей используется акустический резонатор — устройство, обладающее одной или множеством собственных частот.

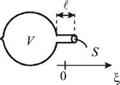
Типичным примером акустической системы, реагирующей лишь на одну частоту, является сосуд сферической формы с открытой горловиной (рис. 5.13), который называется резонатором Гельмгольца. В зад­ней части резонатора имеется еще одно маленькое отверстие в виде сопла, служащее для обнаружения колебаний. Воздух в горловине является колеблющейся массой. При смещении этой массы, на­пример, в сторону сферического обьема V воздух в этом обьеме Рмс. 5.13.

слегка сжимается, и возникающие силы избыточного давления выполняют роль возвраща­ющей силы. Если площадь горловины равна S, а ее длина — 1, то масса колеблющегося столба равна m - р 01S, где р 0 — плотность невозмущенного воздуха. При смещении мас­сы m на расстояние X << 1 (положительное направление оси OX показано на рисунке) плотность воздуха изменяется на величину 6р, удовлетворяющую равенству

*-4І. (5-31)

р 0 V

Согласно (5.7), избыточное давление оказывается равным

(5.32)

Следовательно, уравнение движения столба воздуха принимает вид

d2X d S

m —— = dp • S

dt2

или

(5.33)

Отсюда находим, что собственная частота колебаний столба воздуха в горловине, или частота резонатора Гельмгольца, равна

При объеме резонатора V = 10 3 м3, площади отверстия горловины S = 1 см2 и

её длине 1 = 1 см, скорости звука с = 334 м/c для частоты V 0 получим величину

(5.35)

соответствующую слышимому диапазону звуковых частот.

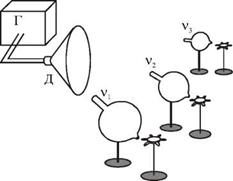
Зависимость собственной частоты колебаний резонатора от его параметров и прежде всего от объема V эффектно демонстрируется в следующем опыте (рис. 5.14). Перед динамиком Д, подключенным к генератору звуковой частоты Г устанавливаются несколько резонаторов, отличающихся своими размерами. Около заднего отверстия каж­дого из резонаторов помещается легкий бумажный пропеллер-вертушка, который мо­жет вращаться вокруг вертикальной оси. При плавном увеличении частоты звукового генератора будет возрастать частота акустической волны, испускаемой динамиком в направлении резонаторов и играющей роль гармонической вынуждающей силы. При последовательном совпадении частоты этой волны V с собственными частотами V1, V 2 и V 3 резонаторов давление воздуха в их объемах будет колебаться с максимальной (резонансной) амплитудой. Из задних отверстий резонаторов будут бить сильные струи воздуха, что фиксируется по началу вращения вертушек сначала у большого, затем у

среднего и, наконец, у самого маленького резонатора, имеющего самую высокую соб­ственную частоту V3 .

Уместно отметить, что при часто­те резонатора V0 ~ 102 Гц длина возбуж­дающей его волны 1 = с/V0 » 3,3 м. Эта длина значительно больше характерных размеров резонатора: 1 >> V1/3. Следова­тельно, не может быть и речи о стоячей акустической волне частоты V0 в самой сферической полости.

Однако и в самой полости можно возбудить стоячие волны с длиной 1 < V1/3 и частотой V - c/1 > c/ V1/3. Если характерный размер резонатора V1/3 ~ 10 см, то час­тоты этих волн V > 3000 Гц. Такой резонатор будет обладать множеством собственных частот в килогерцовом диапазоне.

Наиболее простым в изготовлении акустическим резонатором является дере­вянный ящик или труба, открытые либо с одной, либо с двух противоположных сторон.

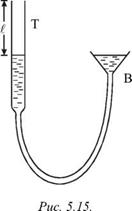
Проделаем следующий опыт. Заполним водой нижнюю часть вертикальной труб­ки Т, используя систему сообщающихся сосудов, и поднесем “t'~ K к ее верхнему концу звучащий на частоте V камертон К (рис. 5.15). Перемещая воронку В вверх, можно добиться уси­ления тонального звука, создаваемого системой «камертон + часть трубы, заполненная воздухом». Это усиление будет на­блюдаться при совпадении частоты V с одной из собствен­ных частот V р резонатора — трубы с воздухом длиной 1,

«закрытой» у нижнего конца. Собственные частоты стоячих волн в таком резонаторе легко подсчитать, если учесть, что на нижнем конце должен быть узел смещений, а на верхнем — пучность. Это возможно лишь для длин волн 1 р, удовлетво­ряющих изложенному в предыдущей лекции условию (4.40):

1 р

1 - (2р - 1)-4р., р - I, II, III, ... ,

V р - — - — (2 р -1). р 1 р 41

когда на длине трубы укладывается нечетное число четвертей длин волн. Соответствен­но, частоты колебаний будут равны

(5.36)

Хотя усиление звука возможно при нескольких длинах воздушного столба 1, однако самым

c

эффективным оно будет при V - VI или 1 ---------- .

4V

Особо подчеркнем, что резонатор создает более благоприят­ные условия для звучания камертона, позволяя перераспределить, а стало быть и усилить звук по определенным направлениям. Именно поэтому в опытах камертоны устанавливают на деревянный ящик, от­крытый с одного конца и настроенный на частоту камертона (рис. 5.16).

Некоторые сведения о музыкальных инструментах. Деревянные деки му­зыкальных инструментов выполняют функции резонаторов, обеспечивая хорошие ус­ловия звучания. Частоты струнных инструментов не зависят от резонатора. Основная частота звука V1 и частоты обертонов зависят только от массы, натяжения и длины струны. Однако тембр звука зависит от способа возбуждения и от реакции резонатора и эффективности, с которой резонатор «поддерживает» эти частоты и посылает соответ­ствующие волны в окружающее пространство.

Рис. 5.17.

b

Валторна

1

12 14 16 v/v„

0

6 8 10 Рис. 5.18.

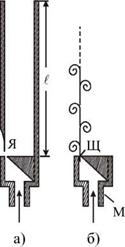
В духовых инструментах формирование звука связано с наличием автоколебаний и зависит как от конструкции инстру- мента, так и от способа, с помощью которого воздух вдувается в инструмент. В качестве иллюстрации рассмотрим качественно процесс возникновения автоколебаний в органной трубе, разрез которой изображен на рис. 5.17а. При равномерном поступлении в мундштук М (рис. 5.17б) воздух проходит через узкую щель Щ, за которой образуется турбулентный поток. Образующаяся при таком те- чении вихревая дорожка является источником «щелевого» тона, основная частота которого обратно пропорциональна периоду следования вихрей Тв. По существу система «мундштук + щель» представляет собой сложную автоколебательную систе- му, теоретическое описание которой — серьезная проблема. Вихри, выходящие из щели, поочередно проходят слева и справа от язычка Я, вызы- вая его вибрацию. Язычок оказывает периодическое воздействие на столб воздуха в трубе. Возникающие в столбе импульсы сжатия, добежав до открытого конца трубы, отражаются в виде импульсов разрежения и возвращаются к щели через время Т = 21 / с (1 — длина тру- бы, с — скорость звука в воздухе), управляя поступлением воздуха через щель. Таким обра- зом, основная частота V1 = 1/ T формируется резонаторной системой. Однако можно вдувать воздух так, чтобы в трубе одновременно существовали два импульса сжатия, и мы услышим звучание трубы на частоте первого обертона (удвоенной частоте). Органные трубы обычно конструируются для звучания на основной частоте. В ду- ховых инструментах возбуждающим вибратором (аналогом язычка Я в органной трубе) можно управлять, чтобы посылать в трубу один или более импульсов, прежде чем первый отразится от открытого конца. Высота звука инструмента опреде- ляется количеством им- пульсов в секунду, отра- женных от открытого кон- ца духового инструмента. Произносимые человеком звуки связаны с тем, что голосовые связки гортани вибрируют под на- пором движущегося возду- ха, а гортань является

объемным резонатором. Как правило, у мужчин объем гортани больше, чем у женщин, поэтому в соответствии с формулой (5.34) мужские голоса более низкие.

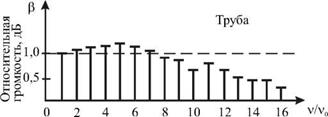
На рис. 5.18 показаны спектры звуков, извлекаемых на трубе и валторне с оди­наковой основной частотой V0 - 440 Гц. По оси ординат отложена громкость b (нор­мирована на громкость волны основной частоты). В спектре звука валторны отсутству­ют частоты V > 10 кГц, поэтому её звук более приглушенный, нежели звук трубы.

Завершая описание основных принципов действия источников звука и музы­кальных инструментов, уместно упомянуть о двух акустических эффектах, с проявлени­ями которых мы практически ежедневно встречаемся.

Эффект Доплера. Наблюдая за проходящим мимо поездом или движущимся автомобилем, мы замечаем, что высота тона подаваемого ими звукового сигнала посто­янно изменяется. Это и есть одно из прояв­И і

лений эффекта Доплера, состоящего в изме - Ло

нении частоты звука при относительном дви - а) С

жении источника и приемника. Рассмотрим и ^ д

это явление несколько подробнее.

Пусть источник И (рис. 5.19а) излу - б)

. 'Pun 5 19

чает монохроматическую (т. е. гармоничес­кую) акустическую волну частоты V0 . Тогда длина этой волны, распространяющейся в воздухе со скоростью с, будет равна:

10 - c/V0. (5.37)

Если теперь источник будет двигаться со скоростью v < с в направлении рас­пространения волны, то волна будет «отрываться» от источника со скоростью с - v, и её длина уменьшится (рис. 5.19б):

1- C—V. (5.38)

V0

Достигнув неподвижного приемника П, эта волна будет воздействовать на него с частотой

V-1-V0 — - V0-V, (5.39)

1 с-v 1 - v/с

которая будет больше исходной частоты V0 . При движении источника в противополож­ном направлении эта частота уменьшится. Именно это изменение частоты тона сигнала мы фиксируем при приближении и последующем удалении поезда или автомобиля.

1+v с /

Изменение частоты будет также и при движении приемника П, однако физичес­кая причина этого изменения состоит в том, что волна с длиной 10 - с / V 0 будет посту­пать в приемник со скоростью v + с (если приемник движется навстречу волне). Следо­вательно, частота воздействия на приемник будет равна

с + v с + v

V - — - V 0 - V 0

и превысит исходную частоту.

В силу различия физических причин, приводящих к изменению частоты при движении источника и приемника, разнятся и формулы (5.39) и (5.40). Однако при v << с,

/ 2 v

как нетрудно убедиться, с точностью до членов порядка — формула (5.39) может

V с 0

быть записана в виде (5.40).

При одновременном движении навстречу друг другу источника со скоростью vи и приемника со скоростью vп обе формулы можно объединить в одну

1 + vп / с

v = v01------------- . (5.41)

1 - Vи / с

При удалении источника или приемника в формуле (5.41) следует изменить знак при соответствующей скорости.

При скоростях v > с формируются ударные волны, и формулы, описывающие изменение частоты, становятся несправедливыми.

Бинауральный эффект. Этот эффект представляет собой психофизиологичес­кое явление, заключающееся в слитном восприятии звуков, принимаемых правым и ле­вым ухом. Он дает возможность определить направление на источник звука и играет существенную роль в музыкальной акустике (стереофония).

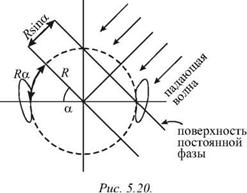
Рисунок 5.20 иллюстрирует этот эффект. Если волна падает под углом к линии, со­единяющей оба уха (пунктиром изображен контур радиуса R, имитирующий голову челове­ка), то волна достигнет левого уха позднее правого, а время задержки составит величину

Аг = ■

R sin a + Ra

(5.42)

где Ra — криволинейный путь, проходимый звуковой волной при огибании ею головы человека за счет дифракции (см. ниже).

Кроме того, поскольку голова частично экранирует звук, то амплитуда волны, достигающей левого уха, несколько уменьшается. Совместное действие этих двух фак­торов дает человеку возможность определить направление на источник звука. Если пе­риод колебаний звуковой волны сравним со временем задержки:

Аг < T/2, (5.43)

то волны, падающие под углом, вызыва­ют колебания барабанных перепонок ле­вого и правого уха со сдвигом фаз 0 < Аф < p, по которому человек и опре­деляет направление прихода волны.

Если положить R =10 см, sin a » 1, то для волн с периодом T< 10-3 с (v > 1 кГц) условие (5.43) не выполняется, и определить направление по сдвигу фазы становится затрудни-

тельно. Однако остается возможность сравнить амплитуды волн, достигающих обоих ушей, и тем самым определить угол a.

Интерференция волн. В предыдущей лекции мы получили уравнение стоячей волны (4.34), описывающее колебания шнура (или иной среды), по которому навстречу друг другу распространяются две гармонические волны одинаковой частоты w и амп­литуды s0 . В результате наложения волн происходит перераспределение в пространстве объемной плотности энергии колебаний. В узлах, где волны встречаются в противофазе, эта энергия равна нулю. В пучностях, напротив, волны складываются в фазе, и энергия максимальна. Явление наложения волн, приводящее к перераспределению в простран­стве объемной плотности энергии колебаний, носит название интерференции.

Интерференция является одним из фундаментальных явлений, присущих вол­нам различной природы (акустическим, электромагнитным, волнам на поверхности жидкости, плазменным волнам и др.). Она была хорошо известна еще во времена Нью­тона, который осуществил замечательный опыт, приведший к открытию закономернос­тей интерференционной картины и получивший название «кольца Ньютона». Эти зако­номерности легко прослеживаются в опытах по интерференции капиллярных волн на поверхности жидкости. В следующей лекции дается описание характера движения час­тиц жидкости в таких волнах и устанавливается связь между частотой, длиной волны и скоростью ее распространения.

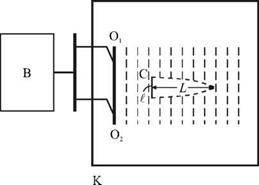
Один из таких опытов выглядит следующим образом (рис. 5.21). В неглубокую кювету К с большой площадью основания наливают воду. Волны на ее поверхности возбуждают с помощью вибратора В, приводящего в периодическое движение два ма­леньких шарика О1 и О2, которые являются точечными источниками волн. Эти шарики слегка погружены в воду и совершают синхронные колебания с частотой V ~102 Гц в направлении, перпендикулярном поверхности воды. От каждого из точечных источни­ков распространяется волна с длиной 1 ~ 3 мм и скоростью с ~ 40 см/с. Гребни этих волн в фиксированный момент времени изображены на рисунке пунктиром. В результа­те наложения волн образуется интерференционная картина, которую удобно наблюдать в стробоскопическом освещении (осве­щая ее вспышками света, следующими также с частотой v ~ 102 Гц). При та­ком освещении волны будут казаться практически неподвижными.

Наиболее сильные возмуще­ния поверхности будут наблюдаться в тех местах, где волны складываются в фазе. Говорят, что здесь располагают­ся интерференционные максимумы.

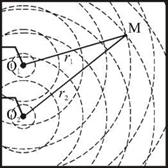
В местах, куда волны приходят в противофазе, поверхность будет практически не возму­щена: здесь располагаются интерференционные минимумы. Возмущение поверхности в произвольной точке M зависит от разности хода Аг = г2 - г1, где r и г2 — расстояния от точки M до соответствующего точечного источника. Действительно, смещение s по­верхности жидкости в точке M можно рассматривать как результат наложения двух си­нусоидальных (т. е. монохроматических) волн, прошедших расстояния r и г2 :

s(t) = s0 sin(wt - kr1 - ф1) + s0 sin(wt - кг2 - ф2). (5.44)

Здесь предполагается, что обе волны в точке M имеют одинаковые амплитуды (хотя это и не совсем верно), и постоянные фазовые добавки ф1 и ф2, так что их разность Аф = ф2 - ф1 не зависит от времени.

Выполняя в (5.44) суммирование, получаем:

(кАг Аф^ . ( k(г + г2) ф, +ф2 ^

s(t) = 2s0cosl-^ + ^~ Isinlwt---------------- 2------------- 2---- I. (5.45)

Если положить для простоты Аф = 0 , то положение интерференционных мак­симумов определяется из условия

= ±1. (5.46)

cos

кАг ~

/

Поскольку k = 2p /1, то последнему условию соответствует разность хода

Аг = г2 - г = ml, (5.47)

где m = 0, ± 1, ± 2, ... .

Каждому максимуму принято присваивать порядковый номер, определяемый соответствующим числом m (максимум нулевого, первого, минус первого и т. д. поряд­ка). Интерференционные минимумы располагаются в тех местах, где

Аг = г2 - г = (2m +1)~, (5.48)

и так же нумеруются (m = 0, ± 1, ± 2, ...).

Рассмотренная интерференционная картина соответствует идеализированной ситуации. Реальные волны даже в лучшем случае являются квазимонохроматическими. Для таких волн амплитуды s0 и фазы ф1 и ф2 являются медленно меняющимися функ-

2р

циями времени (заметные изменения этих функций происходят за время t >> T = —).

ю

Однако, если оба шарика приводятся в колебательное движение одним вибратором, раз­ность фаз Аф в (5.45) остается постоянной, положение интерференционных максиму­мов задается формулой (5.47) и не зависит от времени.

В практически важных случаях источники интерферирующих волн могут быть независимы. В нашем опыте это можно осуществить, если использовать два вибратора, к каждому из которых присоединен маленький шарик. Тогда разность фаз Аф будет так­же изменяться на масштабе времени t, и ее можно записать в виде

где Дф — среднее по времени значение разности фаз, 5(г) — знакопеременная функция. Считая для простоты в (5.45) s0 = const, приходим к выводу, что интерференционная кар­тина, как целое, будет достаточно хаотично смещаться в разные стороны. Если такую кар­тину снимать на кинопленку со временем экспозиции кадра Дг > t, то на каждом кадре будет отпечатана усредненная за время Дг «размазанная» картина. Она может стать совсем неразличимой, если интерференционные максимумы будут смещаться на величины, рав­ные или превышающие расстояния между соседними максимумами. Такая ситуация доста­точно часто встречается при интерференции световых волн. Чтобы полного «смазывания» картины не произошло, очевидно, необходимо выполнение следующего условия:

| 5(0 |<< 2я. (5.50)

Чем лучше выполняется это неравенство, тем выше качество картины. Так, напри­мер, для световых волн t ~ 10-9 +10-12 с, и при визуальном наблюдении (для органов зре­ния Дг ~ 0,1 с) мы всегда регистрируем «размазанную» интерференционную картину.

С качеством картины напрямую связано понятие когерентности интерферирую­щих волн. Когерентность характеризуется безразмерным коэффициентом g (степенью когерентности), который может меняться в интервале 0 < g < 1. Чем выше качество кар­тины, тем больше степень когерентности. Для монохроматических волн, конечно, g = 1.

Этим замечанием о когерентности волн мы здесь и ограничимся, а детальное описание понятия будет дано в курсе «Оптика».

Дифракция волн. В упрощенном смысле под дифракцией понимают круг явле­ний, в которых проявляется отступление от прямолинейного распространения волн. Такое понимание дифракции, вообще говоря, неверно, поскольку прямолинейное распростране­ние волн является лишь определенным приближением. Действительно, специфика любого волнового движения проявляется в том, что это движение, возникнув вначале в ограничен­ной области, стремится распространиться в равной степени во все стороны. Выбором спе­циальной формы этой области можно добиться того, что волна побежит преимущественно в некоторых направлениях. Вдоль одного из таких направлений побежит фрагмент волны, который с определенной точностью можно считать движущимся прямолинейно.

о

ґ

-^-4

о2

K

Для наблюдения основных зако­номерностей дифракции видоизменим характер возбуждения волн на поверхно­сти воды в описанном ранее опыте. В качестве источника волны вместо шари­ков будем использовать пластину O1O2, длина которой 10 = (3 + 5) см, т. е. замет­но превышает длину волны 1 ~ 3 мм (рис. 5.22). В результате по поверхности воды побежит «плоская» волна в направ-

лении, перпендикулярном пластине. Отчетливо наблюдаются две прямолинейные границы T и Г2, отделяющие возмущенную волной и гладкую части поверхности воды. Для этой последней части можно употребить заимствованный из оптики термин: «область геометри­ческой тени». Саму волну часто называют волновым пучком, или лучом. В этом экспери­менте можно считать, что волна распространяется прямолинейно и не заходит в область тени. Это связано с тем, что размер ее волнового фронта 10 >> 1.

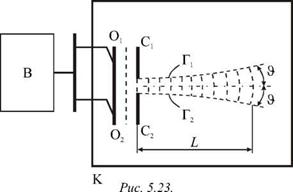
Уменьшим теперь этот размер. Это наиболее просто осуществить, если парал­лельно пластине OjO2 установить две вертикальные стенки С и С2, расстояние 1 меж­ду которыми можно изменять (рис. 5.23).

Если сделать 1 < 51 » » 15 мм, то волна начнет посте­пенно заходить в область тени, а ее фронт будет искривляться. На некотором характерном расстоя­нии L волновой пучок приобре­тет заметную угловую расходи­мость и далее будет распростра­няться по части поверхности, ог­раниченной углом 2J. При уменьшении зазора 1 между стенками угол 2J возрастает, а расстояние L уменьшается. Это отступление от прямолинейного распространения является результатом дифракции и существенно тогда, когда 1 ~ 1.

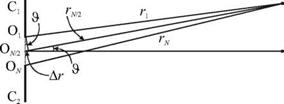
Не составляет труда оценить величины J и L, используя подход, предложенный французским ученым О. Френелем в XIX столетии для объяснения дифракции световых волн. Следуя Френелю, участок фронта падающей волны в зазоре между стенками мож­но рассматривать как цепочку из N >> 1 близко расположенных одинаковых точечных источников O1, O2, ..., ON (рис. 5.24).

Возмущение в любой точке M поверхности воды есть результат интерференции N волн от этих, так называемых «вторичных» источников, и зависит от разности хода всех интерферирующих волн. В практически важных случаях расстояния r, r2 , ..., rN >> 1, поэтому отрезки OjM, O2M, ..., OnM можно считать параллельными. Понятно, что в точку P, лежащую на оси волнового пучка, интерферирующие волны приходят в

M фазе и возмущение повер­хности в ней будет макси - р мальным. Напротив, в точ­ке M волны могут погасить друг друга, если разность хода Dr = rN /2 - r между Рис 5 24 волнами от крайнего ис­
точника Oj и среднего источника 0№2 будет равна 1 /2. Поскольку эта разность, как

1

видно из рис. 5.24, равна —sin «, то

2 д 1-^1

Аг = — sin J = — 22

(5.51)

Аналогично, в противофазе будут приходить волны и от других пар источников (02, 0N/2 + 1; 03, 0N/2 + 2; ...; 0N/2_ 1, 0N). Говорят, что в точке M будет наблюдаться первый минимум дифракционной картины. Не составляет труда написать условие, подобное (5.51), и для других минимумов. Однако, как показывает строгий анализ, более 90% всей энергии переносится волной в пределах угла 2J. Поэтому на рисунке (5.23) границы Г1 и Г2 весьма условны и очерчивают лишь основную, наиболее энергоемкую часть пучка.

Для оценки дифракционной расходимости волновых пучков используется угол «, который при 1 >> 1 оценивается согласно (5.51) по формуле

(5.52)

«-1.

L

г,

21

Рис. 5.25.

Такую расходимость пучок приоб­ретает на некотором характерном расстоя­нии L. Его можно легко оценить из рисун­ка 5.25, на котором пунктиром изображены асимптоты к границам Г1 и Г2. Будем услов­но считать, что на расстоянии L поперечный размер пучка удвоился и стал равным 21. Тогда с учетом (5.52) мы можем записать:

(5.53)

«=1=і

L 1

Отсюда

(5.54)

Величина L называется дифракционной длиной пучка с длиной волны 1 и по­перечным размером 1 . Она определяет масштаб расстояний, на которых развивается заметная дифракция пучка.

Сделаем некоторые оценки.

В опыте, изображенном на рисун­ке 5.22, 1 = 5 см, 1 = 3 мм, и L ~ 80 см.

Это означает, что в кювете дифракция просто не успевает заметно развиться.

При уменьшении 1 (рис. 5.23) до вели­чины 1 = 51 = 15 мм, дифракционная длина пучка L = 7,5 см, и дифракция

становится отчетливо видна. рис 5 26

Если на пути волнового пучка поставить препятствие — стенку С (рис. 5.26), то сразу за стенкой будет тень, однако волна, пройдя расстояние ~ L = 12 /1, обогнет пре­пятствие. Иллюстрацией к сказанному является, например, возможность услышать зву­ковой сигнал автомобиля, находясь позади небольшого строения. Однако за многоэтаж­ный дом звук практически не проникает.