Возбуждение волн
 13 сентября, 2014
13 сентября, 2014  Mihail Maikl
Mihail Maikl |
Распространение возмущений в системе с большим числом степеней свободы. Скорость распространения. Возбуждение волн. Группа волн и ее скорость. Волновое уравнение. Волны в сплошном шнуре. Отражение волн. Возбуждение стоячих волн в шнуре. Моды колебаний. Волны в упругих телах. Поперечные волны. Энергия, переносимая волной. Вектор Умова. Продольные волны. Скорость волн в тонком и толстом стержнях. Отражение и прохождение волн на границах двух сред. Удельное волновое сопротивление. |
|
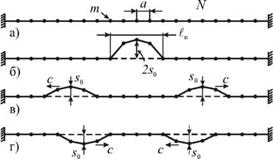
Распространение возмущений в системе с большим числом степеней свободы. Рассмотрим колебания N >> 1 масс на резиновом шнуре (рис. 4.1а). Отклоним несколько масс концов шнура, изменят свою поляр- |
|
С точки зрения повседневного опыта в этом нет ничего удивительного, поскольку смещения группы масс ведут к возникновению упругих сил, стремящихся вернуть эту группу в положение равновесия и одновременно вывести соседние частицы из положения равновесия. С точки зрения описания колебаний «на языке мод» также понятно, что отклонив, а затем отпустив группу частиц, мы возбуждаем много мод. Колебания всех N частиц происходят одновременно на нескольких нормальных частотах ар. Все эти частоты различны, и сумма нормальных колебаний представляет собой биения. Поскольку через время, равное периоду биений, колебания группы частиц в центре шнура восстановятся, то очевидно, что период биений равен упоминавшемуся несколько ранее времени Dt = 21 / с. Определим скорость с, исходя из представления о биениях, как суперпозиции нормальных колебаний. Для этого вначале перепишем дисперсионное соотношение (3.55) в виде / |
|
|
|
Н |
|
1 ------ 1--------------- 0 Рис. 4.1. |
|
Ч |
|
па 1 = 2W sin — |
|
pp N +1 |
|
w p = 2W sin p 2 |
Строго говоря, при наличии многих частот в спектре колебаний, даваемых формулой (4.1), биения не будут периодическими — начальная конфигурация не повторяется. Визуально это будет проявляться в искажении формы бегущих импульсов, если длина импульса l > a (импульс «накрывает» мало частиц), а шнур достаточно длинный. Говорят, что искажение импульса связано с дисперсией «среды» (шнура с массами), по которой импульс распространяется.
|
|
Это искажение будет ничтожным, если 1 и >> а (группа состоит из большого числа колеблющихся масс). Так обычно и происходит при распространении возмущений в твердом теле, где а ~ 10-10 м (расстояние между узлами кристаллической решетки, около которых колеблются атомы).
|
(4.2) |
Если 1 и >> а, то в спектре колебаний доминируют низшие моды, которые характеризуются волновыми числами kp, где p = I, II, III, ... << N. Частоты этих мод получаются из формулы (4.1):
p = I, II, III, ...
p p N +1
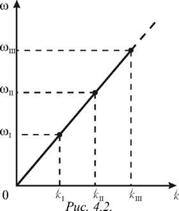
Здесь использовано приближение sin x » x при x << 1. Эта зависимость wp (kp) изображена на рис. 4.2.
Обратим внимание, что низшие частоты располагаются эквидистантно: Dw = wII - wI = wIII - wII = ... Поэтому период биений (см. также формулу (3.14)) получается равным:
2я 2( N +1)
Лг = — = —---------------------------------------------------------------------- (4-- 3)
Dw W ( )
Если учесть, что длина шнура 1 = a(N +1), то скорость движения импульса в среде без дисперсии равна:
|
21 |
Fa
|
(4.4) |
c0 = — = aW = J— . 0 Лг
Если мы будем увеличивать число масс N на шнуре фиксированной длины, тем самым уменьшая расстояние я, то мы сделаем предельный переход к непрерывному распределению масс — т. е. к однородному весомому шнуру, при этом
pj = m / a (4.5)
является массой единицы длины однородного шнура (иногда употребляют термин «плотность единицы длины»). Поэтому окончательно для скорости распространения импульса произвольной формы по шнуру имеем
~F
Например, в случае тонкого резинового шланга с линейной плотностью pj ~ 0,1 кг/м, натянутого с силой F ~ 102 Н, скорость движения импульса получается равной с0 ~30 м/с. Такая сравнительно небольшая величина скорости позволяет легко наблюдать распространение и отражение импульса.
Итак, подведем некоторые итоги.
1. Если пренебречь периодической структурой среды, то скорость с0 распространения импульса не зависит от его формы, а сам импульс при распространении не искажается (нет дисперсии).
2. Если ось x направить вдоль шнура и задать начальное возмущение (в момент t = 0) в виде s(x), то с течением времени возмущение шнура будет иметь вид:
11
2 s(x — с00 + 2 s(x + с00. (4.7)
Первое слагаемое описывает возмущение, бегущее со скоростью с0 в положительном направлении оси х, указанном на рис. 4.1, а второе соответствует импульсу, распространяющемуся в противоположном направлении.
3. У концов невесомого шнура с массами с0 оба импульса отражаются. Отраженный импульс имеет противоположную полярность (направление смещения s) по сравнению с падающим.
Аналогичные граничные условия реализу-
с0
ются для сплошного массивного шнура с закреп-
Рис. 4.3.
ленными концами (рис. 4.3).
4. В области перекрытия бегущих импульсов образуется колебание, называемое стоячей волной. Так мы приходим к понятиям бегущих и стоячих волн, при этом стоячая волна может рассматриваться как суперпозиция волн, бегущих в противоположных направлениях.
Возбуждение волн. Рассмотрим колебания невесомого шнура с грузами, правый конец которого закреплен, а левый под действием внешней силы в момент времени t = 0 начинает смещаться по гармоническому закону:
s(t) = s0sin wt. (4.8)
Под действием этой силы грузы, связанные друг с другом отрезками натянутого шнура, рано или поздно начнут совершать вынужденные гармонические колебания с частотой w. Естественно, что систему грузов (по аналогии с системой с двумя грузами) можно заметно раскачать лишь в случае резонанса, когда частота w совпадает с одной из нормальных частот wp.
Вначале придут в движение грузы вблизи левого подвижного конца шнура, а с течением времени в колебания будут вовлекаться все новые грузы.
Такие колебания представляют собой волновой процесс (волну), распространяющийся «слева - направо» с некоторой скоростью ср. На рис. 4.4 изображены положения колеблющихся масс в некоторый момент времени t0 . Поскольку грузы колеблются «попе-
S/Xjo)
|
|
|
M
Рис. 4.4. |
рек» направления распространения (оси Ox), то волна называется поперечной. Эта волна добежит до правого закрепленного конца шнура и отразится. После этого будут существовать две волны: исходная бегущая (иногда ее называют падающей волной) и отраженная волна, которая бежит навстречу падающей. Спустя время Дг = 21 / ср отраженная волна достигнет левого конца, снова отразится, и «сформируется» мода колебаний. Конфигурация этой моды задается волновым числом к (см. соотношение (4.1)).
Рассмотрим подробнее падающую волну с этим кр. Пространственный период 1р , изображенный на рис. 4.4 как минимальное расстояние между массами, колеблющимися в фазе, называется длиной волны. Длина волны связана с волновым числом kp соотношением:
|
(4.9) |
кр = 2я/1р.
Если силы вязкого трения, приложенные к каждому из грузов, малы, то амплитуды колебаний всех грузов будут одинаковы и равны s0 . Теперь мы можем записать уравнение бегущей волны — уравнение, описывающее смещение любой из масс в произвольный момент времени. Для частоты wp, волнового числа к и амплитуды s0 оно имеет вид:
|
(4.10) |
(xn, г) = s0 sin(w/ - кРх„); xn = a; 2a; ...; na; ...; Na.
Выражение j = - k рхя называется фазой волны. Уравнение (4.10) отражает
тот факт, что все массы колеблются с одинаковой частотой, имеют одинаковую амплитуду s0 , однако эти колебания различаются по фазе j.
Определим теперь скорость ср движения этой волны. Для этого проследим за движением гребня волны, вершина которого в некоторый момент времени находится в точке М. Пусть за время Дг этот гребень сместится на расстояние Дхп >> a. Поскольку на вершине гребня массы имеют максимальное положительное смещение, то фаза их колебаний постоянна и равна
|
|
(4.11)
Поэтому
|
(4.12) |
wpДг - кp Dxn = 0 . Отсюда скорость с p получается равной
|
|
(4.13)
Скорость ср называется фазовой скоростью гармонической волны с частотой = 2pvр. Проанализируем зависимость этой скорости от волнового числа, пользуясь дисперсионным соотношением (4.1). Для этого перепишем его с учетом (4.4) в виде:
|
|
|
Рис. 4.5а. |
|
0 |
Рис. 4.56.
|
p sin —— |
|
|
(4.14)
График зависимости (4.14) называется дисперсионной кривой и изображен на рис. 4.5а.
На этой кривой точками отмечены значения частот wp и волновых чисел k. Пунктиром изображена прямая w = c0 k. Она получается из (4.14) предельным переходом при а ® 0 (непрерывная среда).
Из формулы (4.14) или из рис. 4.5а можно сделать ряд принципиально важных выводов.
|
2 |
1) Из нелинейной зависимости wp = w(kp), описываемой формулой (4.14), следует, что фазовая скорость гармонической волны cp = wp / kp зависит от k (или от wp ):
(4.15)
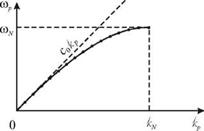
Зависимость (4.15) изображена на рис. 4.5б.
Это явление носит название дисперсии среды по отношению к распространяющейся в ней волне. Эквивалентным является выражение «дисперсия волны в среде». Если фазовая скорость волны не зависит от k, как, например, в случае непрерывной среды, то говорят, что дисперсия отсутствует.
2) Для маленьких волновых чисел (kpa << 1, или l >> а) дисперсия мала. Скорость таких «длинных волн» cp » c0, и среда может считаться сплошной.
3) С увеличением волнового числа kp (а значит и wp ) скорость cp, как это следует из (4.15), убывает. Такое поведение скорости называется нормальной дисперсией. Следует отметить, что в оптике, помимо этой, реализуется и другая ситуация, когда фазовая скорость света в некотором диапазоне частот может возрастать с увеличением частоты. В этом случае дисперсия называется аномальной.
|
a |
4) Дисперсионная кривая заканчивается, когда волновое число и частота достигают максимальных значений kN и wN. Они получаются из (4.14) и (4.1) при N >> 1:
Это означает, что волны с частотой w > wN в такой среде распространяться не могут. Действительно, при частоте w = wN длина волны lN = 2p / kN = 2a. Волны с меньшей длиной волны не могут существовать, поскольку на длине распространяющейся волны должно находиться не меньше двух колеблющихся грузов.
Заметим, что в некоторых случаях, например, при распространении электромагнитных волн в твердом теле и в плазме, кривая дисперсии может начинаться с некоторой точки на оси частот w(0) . В таких средах могут распространяться электромагнитные волны только с частотами w, лежащими внутри интервала w(0) < w < wN.
В качестве примера укажем, что для кристаллов величина F/a ~ 15 Н/м (F — упругая сила, величина которой определяется межатомным взаимодействием). Если принять массу иона равной m ~ 6 • 10-26 кг, то wN = 2.1 ~ 3 • 1013 c-1. Эта частота, как и
V ma
частоты колебаний молекул CO2 и H^O, лежит в инфракрасной области электромагнитного спектра. Поэтому при распространении ИК-излучения в кристаллах ионы могут совершать резонансные колебания. В этом частотном оптическом диапазоне может существовать сильная дисперсия света.
Отметим, что при распространении волн в протяженных средах проблемы «настройки» частоты w внешнего воздействия, порождающего волну, на частоту wp одной из мод среды не существует. Любое воздействие внешней силы, даже сколь угодно близкой к гармонической, на самом деле всегда будет квазигармоническим, характеризуемым узким интервалом частот Aw << w. С другой стороны, для протяженной среды к частоте w будут близки частоты w мод с большими номерами р (p >> 1). Разность частот двух соседних мод Awp = wp+1 - wp, как это легко видеть из рисунка 4.5, будет настолько малой, что Awp << Aw. Следовательно, для любой частоты w внешнего воздействия, прикладываемого к границе среды, по ней побежит волна, которую в ряде случаев можно приближенно считать гармонической:
s(x, t) = s0 sin(wt - kx). (4.16)
Группа волн и ее скорость. Как и внешнее воздействие, волна, возникающая в среде, будет, строго говоря, квазигармонической, т. к. Awp << Aw. Поэтому вместо (4.16) следует записать уравнение волны в более усложненном виде:
s(x, t) = s0(x, t )sin[w0t - k0 x + j0(x, t)]. (4.17)
Здесь амплитуда s0 (x, t) и фаза j0 (x, t) являются медленно меняющимися функциями времени на некотором масштабе времени t (сравните с формулой (3.19)). Естественно, что такая волна представляет собой группу гармонических волн, частоты которых располагаются вблизи основной частоты w0 в пределах интервала Aw » 2p/1. Каждая из волн группы в среде с дисперсией имеет собственную фазовую скорость. В среде с нормальной дисперсией волны большей частоты будут двигаться медленнее, чем волны меньшей частоты. Возникает естественный вопрос: что является скоростью
|
|
группы волн, и если такая скорость существует, то как ее вычислить? Какой физический смысл имеет эта скорость и в чем ее отличие от фазовой скорости?
Чтобы ответить на эти вопросы, рассмотрим для простоты группу из двух волн с одинаковыми амплитудами s0 и с близкими частотами ю1 и ю2 , бегущих в положи-
ю1 + ю2
тельном направлении оси х. Будем считать, что Аю = Ю2 - Ю1 << Ю0 =----------------------------------- ^----- • С такой
ситуацией мы уже встречались при анализе биений двух связанных осцилляторов. Зададим дисперсионные свойства среды дисперсионным соотношением ю = w(k). С его помощью вычислим значения k1 и k 2 двух волновых чисел, соответствующих частотам Ю1 и ю2 . Тогда уравнение группы волн примет вид:
|
Аю Ak 1 x 2 2 v 0 |
/ 4 „ 4 /
sin(w0t - k 0 x). (4.18)
s(x, t) = s0 sin(w1t - k1 x) + s0 sin(w2t - k2x) = 2s0 cos
+ k2
Здесь Ak = k2 - k1, k0 = —
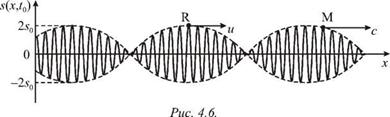
На рис. 4.6 изображена группа из двух волн в некоторый фиксированный момент времени t0 . Выделим две точки: М и R. Первая из них отвечает фиксированному значению фазы фМ = w0t - k0xM, при которой sin jM = 1. Очевидно, что скорость этой точки, определяемая из условия djM = w0dt - k0dxM = 0 , равна
dxM
|
M |
ю0
(4.19)
dt k0
и совпадает с фазовой скоростью волны с частотой ю0 .
Амплитуда квазигармонической волны (4.18) определяется как
, . fАю Ak ^ ....
s0(x, t) = 2s0 cos 1------------------------------ x , (4.20)
V 0
и ее распределение на рис. 4.6 изображено пунктиром в виде медленно меняющейся вдоль х огибающей волны основной частоты ю0. Точка R на вершине этой огибающей будет двигаться со скоростью, отличающейся от с. Действительно, для координаты xR этой точки, как это следует из (4.20), можем записать условие
Аю Ak
1----------------- xR--- = const.
2 2 R
(4.21)
За время dt она сместится на расстояние dxR, которое находится из равенства:
Аю, Ak,
— dt - у^ r = (4.22)
Следовательно, скорость движения вершины огибающей будет равна
|
(4.23) |
|
|
= dxR = Aw dt Ak
|
|
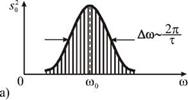
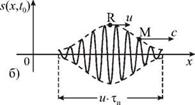
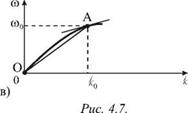
Эта скорость характеризует движение группы волн и называется групповой скоростью. Ее смысл станет еще более понятным, если в пределах интервала Aw в группе будут находиться волны с близко расположенными частотами, как, например, изображено на рис. 4.7а.
|
|
Сама группа имеет вид одного импульса длительностью Ти, распространяющегося вдоль оси х (рис. 4.7б). Импульс будет двигаться с групповой скоростью и = dw / dk. На дисперсионной кривой (рис. 4.7в) эта скорость равна угловому коэффициенту касательной прямой в точке А. «Синусоида» внутри импульса будет его обгонять и двигаться с фазовой скоростью c = w0 / k0 . Численно эта скорость будет равна угловому коэффициенту отрезка ОА. В среде без дисперсии дисперсионная кривая является прямой линией w = ck. Поэтому Aw
w0
(4.24)
Ak
т. е. фазовая и групповая скорости совпадают. В среде с нормальной дисперсией, как это видно из рис. 4.7в, u < c. В среде с аномальной дисперсией кривая w = w(k) должна загибаться вверх и, формально, u > c. Однако обычно эта зависимость настолько нелинейна, что понятие групповой скорости теряет смысл.
Действительно, когда импульс, изображенный на рис. 4.7б, пройдет очень большое расстояние в диспергирующей среде, то форма его исказится, и он растянется в пространстве. В среде с сильной аномальной дисперсией это искажение происходит уже на малых расстояниях, поэтому говорить о распространении импульса как целого с групповой скоростью и некорректно.
Дисперсионное уширение импульсов негативно сказывается, например, на скорости передачи информации (количество бит в единицу времени) посредством коротких световых импульсов, бегущих по волоконно-оптическим линиям связи, длина которых достигает нескольких тысяч километров. Два следующих друг за другом импульса могут расшириться настолько, что сольются в один (станут неразличимыми). Естественно, что приемник, установленный в конце линии, «воспримет» два импульса как один, и часть передаваемой информации будет утеряна.
Волновое уравнение. Уравнение бегущей гармонической волны в однородном шнуре, где дисперсия отсутствует (w = c0k), по аналогии с (4.16) имеет вид:
|
/ x t +------ |
|
(4.25) |
s(x, t) = s0 sin(wt + kx) = s0 sin
Знак «-» соответствует волне, бегущей в положительном направлении по оси Ox, а знак «+» — в отрицательном.
В более общем случае распространения произвольного импульса (группы волн), двигающегося с той же скоростью с0 , уравнение волны можно записать в виде:
|
(4.26) |
|
t+ |
s( x, t) = s
где s(0) — произвольная функция своего аргумента 0 = t + x / c0 .
|
|
Покажем, что закон движения шнура (4.26) и, конечно, его частный случай (4.25) являются решениями некоторого уравнения движения, которое называется волновым уравнением. Это волновое уравнение можно получить предельным переходом из уравнения (3.47).
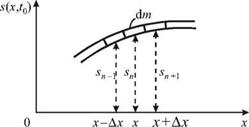
На рис. 4.8 показан фрагмент колеблющегося шнура. На этом фрагменте изображены три отрезка шнура дли - Рис. 4.8.
ной Ax и массой dm каждый. Смещения этих отрезков в некоторый произвольный момент времени равны sn-1 = s(x-Ax, t), sn = s(x, t), sn+1 = s(x + Ax, t). Ускорение цент-
Э 2 s( x, t)
|
рального отрезка s n = ■ |
■. Оно записано в виде второй частной производной фун
at2
|
(4.27а) (4.27б) |
|
lim = iim a®0 a |
|
dx x+— 2 |
|
'n—1 |
|
lim a®0 |
|
= lim Ax®0 |
|
ax |
|
dx |
|
x— |
|
кции s(x, t) по времени. Учтем далее, что s(x + Ax, t) — s(x, t) as Ax®0 Ax ax s( x, t) — s(x — Ax, t) as |
|
Ax |
|
& ax |
|
Обратим внимание, что сила F |
является проекцией на направление
x+dx / 2
смещения s силы F, приложенной к центральному элементу справа (в точке x + dx/2 ).
as
Аналогично, слева (в точке x — dx/2 ) проекция этой силы равна — F--------------------------------------
ax
действующая этих сил, очевидно, определяется приращением первой производной на длине бесконечно малого элемента dx:
|
x— dx /2 |
. Равно-
Если теперь учесть, что dm = pjdx (p1 — плотность единицы длины, или линейная плотность шнура), то (4.28) примет вид волнового уравнения:
|
Э 2 s |
|
(4.29) |
F Э2 s
2
Эt pi Эx
|
Это волновое уравнение является математическим выражением второго закона Ньютона, в котором ускорение единицы длины шнура и действующая на него сила записаны в виде вторых частных производных смещения s по времени и координате соответственно. С математической точки зрения оно является линейным дифференциальным уравнением с частными производными второго порядка. Его решение хорошо известно: им может быть любая функция s(0), аргумент которой «сконструирован» в виде (4.26), а IF скорость c0 = — . Убедимся в справедливости этого утверждения. Для этого вычис- VP1 лим вторые производные в соответствии с правилами дифференцирования функции со x сложным аргументом 0 = t +------------------- : c |
|
0 ds Э0 = ds ; Эs = ds Э0 d0 Эt d0 ’ Эx d0 Эx |
|
ds Эt |
|
ds d0 |
|
1 + — |
|
(4.30) |
|
2 |
|
d2s |
|
d2 s d02 |
|
Э 2 s |
|
Э 2 s |
|
(4.31) |
|
Эt2 d02 Эx2 |
|
Подставляя вторые производные из (4.31) в (4.29), приходим к выводу, что при |
|
c0 = — уравнение (4.29) тождественно удовлетворяется, т. е. функция s(0) действи- IP1 тельно является его решением. Волновое уравнение является одним из фундаментальных уравнений. В разных областях физики это уравнение получается как результат применения соответствующих законов, описывающих поведение систем различной природы (механических, электромагнитных и др.). В общем случае оно описывает распространение волн в трехмерном пространстве и имеет более сложный вид: 22 |
|
Э 2 s Эt2 |
|
222 Э s Э s Э s —2 +-------- 2 +---- 2" Эx Эу Эг |
|
2 |
|
(4.32) |
|
Под s может подразумеваться любая колеблющаяся величина: смещение, скорость, плотность, давление, электрический ток, электрическое напряжение, напряженность электрического и индукция магнитного полей и др. Важно подчеркнуть, что если нам удается получить волновое уравнение (вывести его) для какого-либо процесса, то стоящий перед вторыми пространственными производными множитель сразу определяет квадрат скорости распространения волны в среде без дисперсии. Этим приемом часто пользуются для вычисления скорости распространения волн различной природы. Ниже мы тоже так поступим, когда будем рассматривать волны в твердых телах, жидкостях и газах. |
Отражение волны на конце шнура. Мы уже упоминали в начале этой лекции, что волна, достигнув конца шнура, отразится. Характер этого отражения зависит от условий закрепления конца шнура (граничных условий).
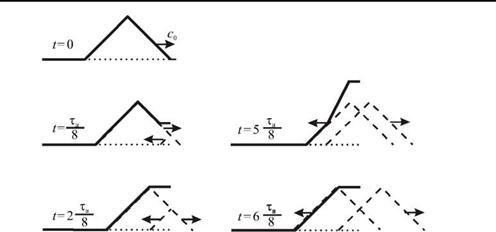
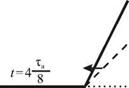
Рассмотрим вначале более подробно процесс отражения импульса от закрепленного конца шнура.
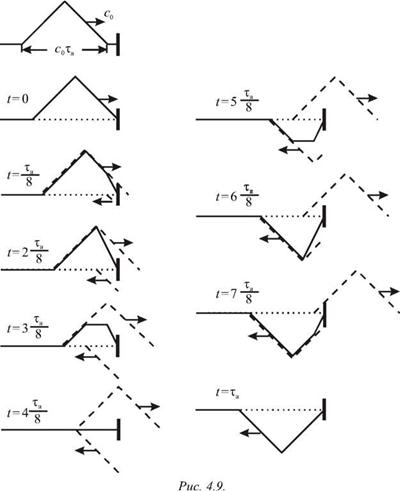
На рис. 4.9 показаны последовательные стадии отражения импульса треугольной формы, где пунктиром изображены «падающий» и «отраженный» импульсы. Если длительность импульса равна tи, то его протяженность вдоль струны равна c0ти. Пусть в момент времени t = 0 он добежит до конца струны. В последующие моменты времени шнур будет воздействовать на кронштейн, к которому прикреплен его конец, с переменной силой, перпендикулярной направлению движения импульса. Эта сила в момент времени t > 0 начинает тянуть кронштейн вверх. В течении времени 0 < t < tи / 2 она остается постоянной, и в момент времени t = ^ / 2 становится равной нулю. По третьему закону Ньютона с такой же силой кронштейн действует вниз на конец шнура. В момент времени t = t и / 2 шнур
|
|
становится прямым. Однако часть шнура длиной сги / 2 продолжает двигаться вниз по инерции. При t >Ти/2 шнур тянет кронштейн вниз, и это действие прекращается при t = t и. Естественно, что кронштейн воздействует на конец шнура с силой, направленной вверх, тормозя движение его элементов вниз. Окончательно поперечное действие шнура на кронштейн прекратится при t > tи, когда сформируется отраженный импульс, имеющий противоположную (по отношению к падающему) полярность.
|
Рис. 4.Ю. |
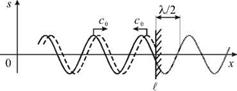
Если по шнуру бежит гармоническая волна, то по достижении закрепленного конца шнура возникает обращенная отраженная волна. Чтобы учесть изменение ее полярности, в аргумент уравнения отраженной волны добавляют фазовый сдвиг фотр = р. Поэтому говорят, что в этом случае при отражении фаза волны скачком меняется на р, или «теряется полволны». В общем случае при произвольных граничных условиях сдвиг фазы фотр может меняться в интервале 0 < фо1р < р. Поясним сказанное простейшим расчетом.
Пусть по шнуру бежит гармоническая волна. Достигнув конца шнура при x = 1, она будет отражаться (рис. 4.10). Смещение любого участка, имеющего координату x < 1, определяется как суперпозиция бегущей и отраженной волн:
s(x, t) = s0 sin(wt — kx) + s0 sin[wt — k(21 — x) + фотр]. (4.33)
В (4.33) учтено, что отраженная волна, во-первых, проходит расстояние «туда и обратно», равное 1 + (1 - x) = 21 - x, и, во-вторых, приобретает сдвиг фазы фотр при ее отражении. Проведем суммирование в (4.33) и получим:
|
ф отр |
|
(4.34) |
|
s(x, t) = 2s0 cos |
|
sin |
|
wt — k1 + фотр 2 |
Полагаем, что амплитуда волны s0 остается постоянной при распространении и не меняется при отражении.
Это выражение является уравнением стоячей волны. Основные ее характеристики могут быть сведены к следующим:
1. В стоячей волне все участки шнура колеблются с одинаковой частотой w и в фазе, однако амплитуда этих колебаний меняется вдоль шнура, т. е. стоячая волна является модой колебаний.
2. Амплитуда колебаний в стоячей волне получается из (4.34) равной:
|
ф отр |
|
k (1 — x) + |
|
(4.35) |
|
A(x) = 2s0 cos |
Из этого выражения видно, что некоторые участки шнура колеблются с амплитудой, равной 2s0 . Это так называемые «пучности» стоячей волны. С другой стороны, существуют участки, которые остаются неподвижными, т. к. для них амплитуда А = 0. Это так называемые «узлы» стоячей волны.
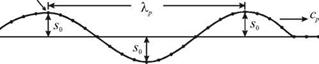
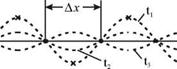
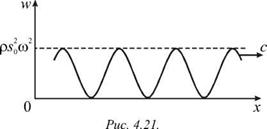
На рис 4.11 изображены
|
Рис. 4.11. |
|
x |
смещения фрагмента струны для трех последовательных моментов времени ti, t2 и t3. Нетрудно показать, что расстояния между двумя со-
седними узлами, указанными точками, равно расстоянию между двумя соседними пучностями, отмеченными крестиками, . р 1
и составляет величину Дх = — = —.
3. Все части шнура, лежащие между двумя соседними узлами, совершают колебания в фазе. При переходе через узел фаза колебаний скачком изменяется на р, что соответствует изменению знака А(х).
4. На конце шнура (х = 1) амплитуда
|
(4.36) |
A(1) = 2s0 cos
Для закрепленного конца шнура А(1) = 0 и фотр = р. На рис. 4.10 показан участок в полволны, который «теряется» при таком отражении. Расположенная правее этого участка часть волны, изображенная пунктиром в области х > 1, после поворота направления распространения как раз и будет являться волной, отраженной в закрепленной точке х = 1.
Обратимся теперь к отражению волны от свободного конца шнура. Технически это можно реализовать, если конец шнура привязать к тонкой и легкой нити, которая служит лишь для создания натяжения шнура с силой F.
Процесс отражения треугольного импульса от свободного конца шнура показан на рис. 4.12. Обращают на себя внимание два обстоятельства:
1. Отраженный импульс сохраняет ту же полярность, что и падающий. Это связано с тем, что при движении свободный конец будет тянуть вверх прилегающие к нему слева участки шнура, и, в результате, будет возбужден отраженный импульс, в котором элементы шнура также смещены вверх. В случае гармонической волны отраженная волна находится в фазе с падающей. Образующаяся стоячая волна будет описываться уравнением (4.34), в котором фотр = 0 .
2. Конец шнура совершает «взмах», величина которого вдвое превышает амплитуду импульса в его середине. Для гармонической волны на конце шнура (х = 1) образуется пучность стоячей волны. Это следует из формулы (4.36), в которой следует положить фотр = 0 .
Возбуждение стоячих волн в шнуре. Моды колебаний. Пусть кронштейн, к которому привязан левый конец шнура, совершает гармонические колебания s(t) = Х0 sin wt, где X0 — очень малая амплитуда. Поэтому левый конец шнура можно считать закрепленным. По шнуру побежит гармоническая волна (рис. 4.13), которая после отражения от правого закрепленного конца приобретет сдвиг фазы, равный р. Добежав до левого конца, она еще раз отразится, а сдвиг фазы станет равным 2р.
|
|
|
|
|
|
|
|
|
t=7- |
|
|
|
t=t |
Рис. 4.12.
Двукратно отраженная волна наложится на постоянно бегущую вправо гармоническую волну. Если сдвиг фазы колебаний у этих волн будет кратным величине 2р, то результатом наложения будет волна, амплитуда которой превышает амплитуду Х0 исходной бегущей волны. Таким образом, бегущая волна усилится. Если бы не было потерь энергии, то нарастание амплитуды при многократном отражении было бы неограниченным. Однако потери, как мы не раз видели, также увеличатся с ростом амплитуды. Поэтому колебания установятся: в систему будет закачано некоторое количество энергии, а дальнейший приток ее будет равен диссипации.
|
|
Определим частоту внешнего воздействия w, с которой следует двигать левый кронштейн, чтобы обеспечить максимальное усиление волны. Поскольку бегущая гармоническая волна может рассматриваться как рис 4 13 набор следующих друг за другом
со скоростью с0 импульсов разной полярности, то мы проследим за усилением любого из них (например, заштрихованного на рис. 4.13). Время движения импульса (для определенности точки А в его начале) по шнуру туда и обратно равно At = 21 / c0 . Учтем далее, что после двух отражений этот импульс два раза обратится. Для его усиления необходимо, чтобы в момент t = At левый конец шнура проходил положение равновесия и двигался при этом вверх:
|
(4.37) |
s(At) =X0sin(wAt) = 0, s (At) = X 0 w cos(wAt) = +X 0 w.
Поэтому частота w должна удовлетворять условию
wp At = 2pp, (4.38)
гдеp = I, II, III, ... .
Отсюда

|
pc0 1 |
|
wp = |
(4.39)
|
|
|
|
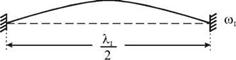
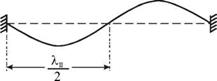
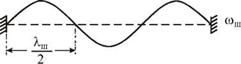
Конфигурацию колеблющейся струны на частотах (4.39) можно легко нарисовать, когда амплитуды бегущей и отраженной волн не меняются вдоль шнура и равны между собой. Очевидно, что это будут стоячие волны, рассмотренные нами выше и соответствующие одинаковым граничным условиям: на обоих концах шнура должны быть узлы смещения.
|
Рис. 4.14. |
Для примера на рис. 4.14 изображены три возможные конфигурации шнура в момент времени, когда смещения элементов шнура максимальны. Колебания, соответствующие этим конфигурациям, являются нормальными колебаниями (модами), а частоты wp wn, Юш — нормальными
частотами. Если действие внешней силы прекратится, то эти колебания будут продолжаться как собственные, пока не затухнут.
Условие (4.39) можно переписать в более наглядном виде, если перейти от частоты wp к длине волны lp = 2pc0 / wp :
(4.40)
Это условие означает, что при нормальных колебаниях на длине шнура должно укладываться целое число полуволн. Легко теперь видеть, что каждая из мод может быть возбуждена, если прикладывать силу нужной частоты к любому участку шнура, за исключением тех, которые совпадают с узлами данной моды.
1 = p— . 2
Видоизменим граничные условия и сделаем оба конца шнура свободными (привяжем их к натянутым легким нитям). Подсчитаем частоты вынуждающей силы, на которых возбуждаются стоячие волны (моды). Учтем, что после двух отражений импульс не меняет свою полярность, поэтому условие (4.40) останется прежним.
|
|
|
wI |
|
Wii |
|
|
|
Wii |
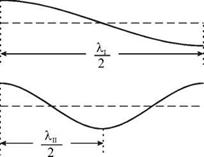
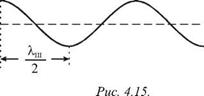
На рис. 4.15 показаны конфигурации мод для шнура со свободными концами. Видно, что при нормальных колебаниях на длине шнура также должно укладываться целое число полуволн, но таким образом, чтобы на концах шнура были пучности.
Закрепим теперь только левый конец шнура и будем двигать кронштейн с малой амплитудой X0 . Условие оптимального возбуждения стоячих волн (мод) получается из тех соображений, что импульс обращается только при отражении от левого конца шнура. Для усиления импульса необходимо, чтобы левый конец в момент времени t = At двигался вниз, проходя положение равновесия:
|
(4.41) |
s(At) =X0sin(wAt) = 0, s(At) = X0w cos(wAt) = - X0 w Поэтому частота w должна удовлетворять условию
wp At = (2 p - 1)p, (4.42)
где p = I, II, III, ...
Отсюда
|
(4.43) |
w p =-pr°(2 P -1).
p 21
Последнее условие становится более наглядным, если перейти к длине волны 1
1 = (2p -1)-^,
(4.44)
4
где p = I, II, III, ... .
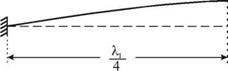
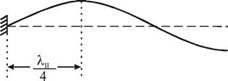
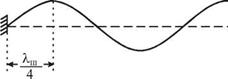
Соответствующие три низшие моды изображены на рис. 4.16. Очевидно, что это будут стоячие волны, отвечающие разным граничным условиям: на левом конце должен быть узел, а на правом — пучность. На длине шнура при этом укладывается нечетное число четвертей длин волн.
Замечание. При возбуждении моды мы задавали закон движения закрепленного конца шнура в виде s(t) = X0 sin wt, что может вызвать у читателя некоторое недоумение — как может двигаться закрепленный конец? Однако амплитуда колебаний X0 обычно значи-
|
|
|
ю, |
тельно меньше амплитуды колебаний в пучностях, поэтому незначительно вибрирующий конец шнура может рассматриваться, как неподвижный.
|
|
|
ю |
Волны в упругих телах. Как
|
|
|
ю |
|
Рис. 4.16. |
мы видели, силы взаимодействия между соседними колеблющимися элементами шнура обеспечивают распространение в нем волн. В упругих телах такие силы сводятся к касательным и нормальным напряжениям, возникающим при деформациях сдвига и растяжения (сжатия). Этим деформациям соответствуют 2 типа волн: поперечные и продольные. Рассмотрим эти волны по отдельности.
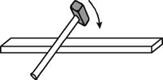
Поперечные волны. Если по стержню, изготовленному из упругого материала, ударить молотком в его средней части (рис. 4.17), то к его концам побегут импульсы, как это имело место в шнуре с грузами, изображенном на рис. 4.1. Однако поперечные смещения частиц стержня будут незаметны для глаза, поэтому для регистрации бегущих по стержню возмущений требуются специальные методы.
Поскольку дисперсия волн механической природы в сплошной среде отсутствует, то скорость их распространения можно рассчитать с помощью волнового уравнения.
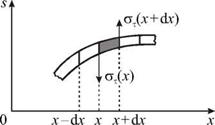
На рис. 4.18 показан фрагмент колеблющегося стержня. На средний элемент длиной dx действуют касательные напряжения (слева от (x) и справа от (x + dx)), величины которых пропорциональны деформациям сдвига соседних элементов:
|
Ox |
|
(4.45) |
sT (x) = G tg g( x) = G
Ot (x + dx) = G tg g( x + dx) = G
|
x+dx
|
Здесь G — модуль сдвига, g — угол сдвига.
|
|
Если площадь поперечного сечения стержня равна S, то масса элемента dm = Spdx (р — плотность материала). Следовательно, уравнение его движения может быть записано в виде:
|
"ds |
ds |
||
|
dx V |
x+dx |
dx |
x 0 |
|
S. |
|
(4.46) (4.47) |
Spdx £ = G
Поделив обе части (4.46) на S и dx, получаем волновое уравнение
d2 s = G d 2 s dt2 p dx2
|
Его решением, как мы уже отмечали выше, является любая функция аргумента 0 = t + x / c : |
|
/ x t +— |
|
s(x, t) = s(0) = s а скорость распространения волны G |
|
(4.48) |
|
(4.49) Процессы распространения и отражения поперечных волн в стержне полностью аналогичны таковым в однородном натянутом шнуре, поэтому мы их рассматривать не будем. Сконцентрируем внимание на закономерностях переноса механической энергии бегущей волной. |
|
Энергия, переносимая волной. В лекции по деформациям упругих твердых тел мы отмечали, что при деформации сдвига в единице объема тела запасается потенциальная энергия |
|
4 2 dx / |
|
1 |
|
1 |
|
(4.50) |
|
w =- Gg2 =- G |
|
называемая объемной плотностью энергии деформации сдвига. В (4.50) полагаем ds |
|
g» tgg = |
|
dx |
|
Помимо этого, единица объема с массой, равной p, и колебательной скоростью v = ds / dt имеет кинетическую энергию |
|
ds 2 |
|
1 2 1 wv = — р v = — р v 2 2 Полная энергия единицы объема равна |
|
(4.51) |
|
dt v / |
|
/_ds 4 2 dx V У |
|
ds 2 dt V У |
|
1 w = wg + wv = - |
|
(4.52) |
|
+p |
Покажем, что в бегущей волне (4.48) wy = wv. Для этого вычислим производные:
|
+ — c v |
|
(4.53) |
|
dt d0 dt d0 |
|
ds ds d0 ds (_ 1 ^ ds ds d0 ds |
|
dx d0 dx d0 |
|
Из (4.53) получаем Os _ 1 Os v т—= +—т—, или g= + —. (4.54) Ox c Ot ' c v 7 Отметим, что в бегущем волне деформации g какого-либо элемента пропорциональны его колебательном скорости v Возводя в квадрат левое равенство (4.54), деля его пополам и учитывая, что с2 = G / р, получаем |
|
'g = w— . (4.55) Равенство величин Wg и w— позволяет записать полную плотность энергии w в виде: (4.56) Поскольку волна движется, то она осуществляет перенос механической энергии. Так, например, за время Dt через площадку единичной площади, заштрихован- DW = wcDt. В физике используют понятие плотности потока Согласно (4.57), эта плотность равна |
|
G |
|
1 |
|
Os |
|
Os Ot |
|
1 = 2 Р |
|
Ox v / |
|
w = 2 wg = 2w— |
|
(4.57) |
|
/ A'A A |
|||
|
1 > |
■і |
f |
|
cDt ------------ Рис. 4.19. |
|
►с ♦•х |
r DW
|
(4.58) |
J =----------- = wc
Dt
|
dS |
|
Рис. 4.20. |
|
|
и имеет размерность [J] = Дж/(м2 • с).
Если площадка имеет площадь dS, а ее нормаль n составляет с направлением распространения волны (осью Ox) угол а (рис. 4.20), то количество энергии, переносимое волной через эту площадку за единицу времени (поток энергии) равен
dF = wc • dS cos a. (4.59)
Профессором Московского университета Н. А. Умовым в 1874 г. был введен вектор плотности потока энергии
J = wc, (4.60)
получивший название вектора Умова. С его использованием поток dF может быть записан в виде
dF = J • dS = JdS cos a, (4.61)
где dS = dS • n.
С подобным представлением потока вектора скорости мы встречались при изучении движения жидкостей.
|
Удобство вектора Умова становится особенно ощутимым, когда волна распространяется в трехмерном пространстве. Тогда поток энергии через произвольную поверхность S выражается в виде интеграла по этой поверхности: F = Jj • dS. (4.62) S Последняя формула будет использована ниже. Подсчитаем среднее за период значение вектора Умова для бегущей вдоль стержня поперечной гармонической волны s(x, t) = s0 sin(wt - kx). (4.63) Обьемная плотность энергии (сумма потенциальной и кинетической энергий) равна |
|
(4.64) В некоторый момент време- мальной величины ps0 w2 . Поэтому удобно пользоваться средним значением Jза пери- — |
|
Г 1^7 1 I = — J Jdt = — cpw |
|
0 |
|
'ds 42 |
|
= ps0 w2 cos2 (wt - kx) . |
|
|
|
w = р |
|
dt |
|
2 s 2 s0 . |
|
(4.65) |
Важно отметить, что интенсивность пропорциональна квадрату амплитуды.
В стоячей волне нет переноса энергии, т. к. она является суперпозицией двух бегущих волн, переносящих одинаковое количество энергии в противоположных направлениях. Однако, локальное движение энергии в ограниченном пространстве между соседними узлами все же происходит. В самом деле, запишем уравнение стоячей волны (4.34), опустив в нем постоянные фазовые добавки фотр /2 и kl:
|
(4.66) (4.67) |
s(x, t) = 2s0 cos kx sin wt.
Обьемная плотность энергии деформации сдвига равна:
|
1 G wg = — G |
ds 2
= 2s0 k 2G sin2 kx sin2 wt,
dx
а обьемная плотность кинетической энергии выражается как:
|
2 |
|
/ds Hi у G P |
|
>«,=2p 2 w2 поскольку c = —2- : |
|
= 2s0w2p cos2 kx cos2 wt = 2s2 k 2G cos2 kx cos2 wt |
|
22 |
|
(4.68) |
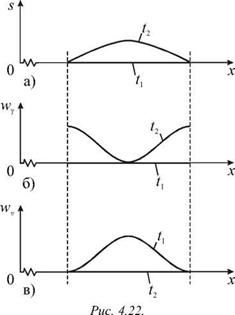
Локальное движение энергии наглядно демонстрирует рис. 4.22, на котором показан фрагмент стоячей волны в моменты времени t1 = 0 и t2 = t1 + T /4 (а) и соответствующие распределения wg (б) и wv (в).
Видно, что при t = tj, когда элементы стержня проходят положение равновесия и имеют максимальные скорости, деформация отсутствует (wg = 0), а вся энергия запасена в виде кинетической энергии wv и локализована вблизи пучности. Однако через четверть периода колебаний частицы стержня сместятся на максимальные расстояния и остановятся (wv = 0). Энергия будет запасена в виде потенциальной энергии Wg и локализована вблизи узлов. Это означает, что энергия из области вблизи пучности за четверть периода колебаний перетекает в обе стороны по направлению к узлам.
|
|
Затем она движется в обратном направлении, и этот процесс повторяется многократно. Поток энергии через узлы отсутствует. Среднее за период значение потока энергии через любое сечение x = const будет равно нулю (I = 0).
|
ct |
|
а) С
|
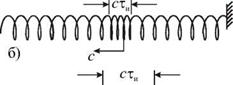
Продольные волны. Такие волны могут быть возбуждены ударом молотка по одному из торцов упругого стержня. Возмущение, распространяющееся вдоль стержня, визуально незаметно, однако основные закономерности такого волнового процесса можно смоделировать, если вместо стержня использовать длинную пружину с большим диаметром витков (рис. 4.23). Если эту пружину подвесить горизонтально на нескольких нитях (не показанных на рисунке) и резко ударить ладонью по левому торцу, то по ней побежит импульс сжатия с некоторой скоростью с. На рис. 4.23а этот импульс имеет длину ct и (ти — длительность импульса, равная длительности удара). Добежав до правого конца пружины, он отразится, при этом, если конец закреплен (рис. 4.23б), то отраженный импульс будет также импульсом сжатия. Если правый конец свободен, то отраженный импульс будет импульсом растяжения (рис. 4.23в). Он возникает в момент смещения вправо свободного конца пружины, когда до него добежит импульс сжатия. Эта ситуация напоминает смещение свободного конца шнура. Отметим, что в рассмотренном случае смещения витков пружины происходят вдоль направления распространения волны, поэтому волна называется продольной.
Рассмотрим теперь распространение импульсов сжатия и растяжения в стержне. Мысленно разобьем x стержень на ряд элементов длиной dx каждый. При распространении продольной волны концы каждого элемента, отмеченные на рис. 4.24 сплошными линиями, будут смещены в новые положения, отмеченные пунктиром. Эти смещения s будем считать положительными, если они происходят в положительном направлении оси Ox, и отрицательными — в противоположном случае.
Пусть левый конец некоторого элемента, имеющий координату х, сместился в данный момент времени t на расстояние s(x, t), а правый конец — на s(x + dx, t). Деформация растяжения (сжатия) определяется относительным удлинением элемента dx:
|
(4.69) |
s( x + dx, t) — s( x, t) 5s dx 5x
e( x, t) = -
Отметим, деформации растяжения соответствует e > 0, а сжатия — e < 0 .
В отличие от поперечной волны, при растяжении (сжатии) уменьшается (увеличивается) плотность среды р. Ее можно представить в виде
р = ро + 5р; |5р |<<ро. (4.70)
Здесь 5р — малая добавка к равновесной плотности р0 , причем 5р может быть как положительной, так и отрицательной. С учетом постоянства массы деформируемого элемента dx можем записать
р0^ = (р0 +5р)[^ + s(x + dx, t) — s(x, t)] = (р0 +5р^(1 + e). (4.71)
Раскрывая скобки и пренебрегая малой величиной e • 5р, находим
5р
|
= —e. |
(4.72)
|
•:«$i |
#г:: |
: |
‘І |
||||||||||||||
|
Ш: |
щ |
.Л;:.) і?^ |
,-.:ґ./ ‘ |
: ■. ■ 1 |
|
ИМПУЛЬС СЖАТИЯ |
|
ИМПУЛЬС РАСТЯЖЕНИЯ |
|
|
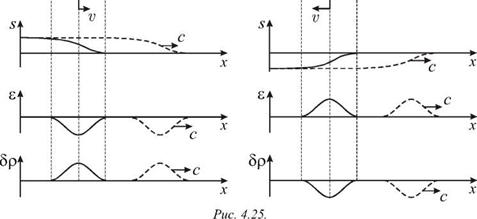
Спустя некоторое время t после удара по торцу стержня (или после резкого оттягивания этого торца) распределение смещений s, деформаций e и возмущений плотности 5р в бегущих импульсах сжатия и растяжения будут иметь вид, показанный на рис. 4.25. Пунктиром показаны распределения всех величин в один из последующих моментов времени.
Уравнение волны, бегущей вдоль оси Ox, в обоих случаях имеет вид s(x, t) = s(t - x/c). По аналогии с (4.54) деформация e = —s / —x и колебательная скорость v = —s / —t элемента связаны соотношением
|
(4.73) s„(x>0 s„(x+dx,0 |
—s 1 —s v
—x = - С —, или e=-c.
|
7г |
|
I I I I |
Подчеркнем, что в импульсе сжатия (e < 0) скорость v совпадает по направлению со скоростью с, а в импульсе растяжения они имеют противоположные направления.
|
x x + dx x Рис. 4.26. |
Рассчитаем скорость распространения продольных волн. На рис. 4.26 изображен фрагмент стержня и показан его элемент dx, к концам которого приложены нормальные напряжения on. Уравнение движения элемента с поперечным сечением равным S имеет вид:
—2 s
dm —у = S[on(x + dx, t)-on(x, t)], (4.74)
—t
где dm = Po Sdx. Чтобы (4.74) преобразовать к волновому уравнению, необходимо связать напряжения on с деформациями элементов стержня. Наиболее просто это можно сделать для тонкого стержня.
Скорость волн в тонком стержне. Если стержень тонкий, то деформации и напряжения вдоль координаты x связаны известным законом Гука:
|
o n (x, t) = E Is —x |
|
—s o n (x + dx, t) = E— —x |
|
(4.75) |
|
x+dx |
где E — модуль Юнга.
Подставляя (4.75) в (4.74) и производя деление на р0Sdx, получаем волновое уравнение:
|
(4.76) |
—2s E —2
—t 2 р0 —x2
Скорость продольных волн получается равной
(4.77)
Эта скорость превышает скорость поперечных волн (см. формулу (4.49)), поскольку E > G. По порядку величины обе скорости совпадают и для различных материалов преимущественно лежат в диапазоне c ~ (103 +104) м/с.
|
Скорость волн в толстом стержне. Пусть вдоль оси толстого стержня (оси х) распространяется продольная волна, при этом колеблются элементы стержня, находящиеся вблизи его оси. Один из таких элементов показан на рис. 4.27. Под действием нормального напряжения о1 относительное удлинение Є1 определяется первым уравнением (1.27), приведенным в лекции по механике упругих тел: Oi - (02 +оз)т |
|
Єї =- |
|
x2 |
|
|
|
x, x |
x x+dx
Рис. 4.27.
(4.78)
Это уравнение отражает тот факт, что при удлинении элемента dx, изображенного на рис. 4.27, площадь его поперечного сечения уменьшается (связь продольной и поперечной деформаций определяется коэффициентом Пуассона 0 <m< 1/2). Этот элемент потянет к оси стержня окружающие его элементы, развивая напряжения O2 и O3. Эти элементы (лежащие между плоскостями x = const и x + dx = const) начнут приходить в движение: сначала — находящиеся вблизи оси стерж

|
L/2 |
|
(L — поперечный |
ня, а затем и элементы, близкие к поверхности. Через время At =
размер стержня, с — скорость распространения возмущения) все элементы сместятся, и напряжения о 2 и о 3 исчезнут.
Если длительность Г и импульса, распространяющегося вдоль оси стержня, велика, так что ти >> At = — , то в (4.78) можно не учитывать о2 и о3. Скорость такого длин - 2с
ного импульса будет определяться формулой (4.77). Такой режим можно реализовать, если
L << сГи. (4.79)
Условие (4.79) означает, что поперечный размер стержня L значительно меньше длины импульса. Такой стержень можно считать тонким. Если речь идет о гармонической волне, распространяющейся вдоль стержня, то условие (4.79) имеет вид
L <<1, (4.80)
где 1 = сТ — длина волны, Т — период колебаний. Так, например, для стального стержня с = — ~ 5000 м/с. При частоте V = 5000 Гц, 1 = с / V ~ 1м, поэтому стержни с
поперечным размером L ~ 1 см могут считаться тонкими.
Если длительности импульса ги << At = — (стержень толстый), то в (4.78) сле-
2с
дует учесть о2 и о3. Чтобы найти связь е1 и о1, вместе с уравнением (4.78) запишем аналогичные для Є 2 и е3 и сложим все три уравнения:
Є1 +Є 2 +Є3 = «° +°2- +Е’3)(1 - ЗД. (4.81)
Для краткости выкладок введем средние значения
11
Є = 3 (Є1 + Є 2 +Є3); о = 3(01 +02 +03).
Тогда (4.81) перепишется в виде
Є = о(1 - 2m). (4.82)
E
С учетом (4.82) уравнение (4.78) видоизменяется:
3me 1 + m
Є1 +—-— = — о1. (4.83)
1 1 - 2m E 1
Если положить в толстом стержне Є2 = Є3 = 0, то є = є1/3 , и искомая связь получится в виде:
Є Qj о1(1 + m)(1- 2m) (4 84)
1 E/ (m) E (1-m) ' '
В этом случае связь деформации и напряжения определяется как модулем Юнга
Е, так и следующей функцией коэффициента Пуассона
/(m) = (1 1)-1m 2 ). (4.85)
(1+m)(1 - 2m)
Легко убедиться, что при любых возможных значениях коэффициента Пуассона /(m) > 1 . Поэтому скорость продольной волны в этом случае
—/ (m) (4.86)
р0
превышает скорость волны в тонком стержне. Величину E • /(m) обычно называют «модулем одностороннего растяжения».
Отметим, что наиболее сложен анализ для промежуточного случая, когда L ~ 1. Для волн с такой длиной волны имеет место дисперсия (фазовая скорость гармонической волны зависит от ее частоты). Распределение амплитуды волны в поперечном сечении стержня вдоль осей x2 и x3 аналогично распределению амплитуды для шнура длиной L со свободными концами при нормальном колебании. Стержень в этом случае выполняет роль волновода. При его плавном изгибании волна распространяется вдоль его оси.
Продольные волны переносят энергию, и для них справедливы все рассуждения и выводы, полученные для поперечных волн. Формально во все выражения для плотности энергии w, вектора Умова Jи др. следует вместо модуля сдвига G подставить модуль Юнга Е или E • /(m) . Предоставляем читателю проделать это самостоятельно.
Явления на границе раздела двух сред. Рассмотрим подробнее прохождение продольной волны через границу раздела двух упругих сред при нормальном падении волны на эту границу.
|
|
|
Ei, pi |
|
Рис. 4.28. 1-я среда (падающая + отраженная волна) s1(x, t) - s01 sin(wt - k1 x) + s01 sin(wt + k1 x) |
Пусть продольная волна распространяется со скоростью С1 - V E1/ р1 в среде с модулем Юнга E1 и равновесной плотностью р1 (рис. 4.28). Опыт показывает, что эта волна на границе раздела двух сред (х = 0 на рисунке) частично отражается и частично проходит во вторую среду, которая характеризуется параметрами E2 и р 2 . Следовательно, можем записать 2-я среда
(прошедшая волна) s2(x, t) - s02 sin(wt-k2x) (4.87)
Здесь w — частота, s01, s01 и s02 — амплитуды падающей, отраженной и прошедшей волн соответственно, k1 - w/ c1 и k2 - w/ c2 — соответствующие волновые числа.
Чтобы найти соотношения между амплитудами трех волн, определяющие отражательную и пропускательную способность («прозрачность») границы раздела, запишем два условия, которые должны выполняться на границе раздела при х = 0.
Первое — это условие неразрывности вещества:
S (0,t) - s2(0, t). (4.88)
Второе — равенство напряжений:
o1(0,t) - о2(0,t), или E1e1(0,t)-E2e2(0,t). (4.89)
С учетом (4.87) из этих условий получаем:
S01 + s01 - s02,
- S01E1k1 + s01E1k1 - -s02E2k2.
В акустике фундаментальным является понятие импеданса, или удельного волнового (акустического) сопротивления материала. Эта величина z определяется как:
(4.90)
|
-о. v |
|
(4.91) |
сжимающее напряжение
колебательная скорость
Импеданс легко можно выразить через характеристики материала, воспользовавшись формулой (4.73):
|
Отсюда |
0 v (4.92)
-о E
z — - pc.
vc
С использованием этой величины и выражений для к 1 и к2 условия (4.90) примут вид:
s01 + s01 - s02
і, - (4.94)
- s01 z1 + s01 z1 - - s02z2.
Отсюда получаем искомую связь между амплитудами волн:
1 - z2 / z1
s01 ----------------- —- s
т, , 015 s02 -" : s01. (4.95)
1 + z2 / z1 1 + z2 / z1
Для практических целей пользуются коэффициентами отражения R и пропускания Г, характеризующими отношение интенсивностей отраженной и прошедшей волн к интенсивности падающей волны. Эти коэффициенты получаются из (4.95) с учетом (4.65):
|
2 |
|
R = L - І1 |
|
01 |
|
02 |
|
(4.96) |
|
01 |
|
01 |
|
2 1- z 2/z1 1 + z 2 / z1 |
|
T - — - — І |
|
1 |
|
4(z2 / z1) (1 + z2 /z1)2 |
|
т 1 2 2 1 2 2 І - 2 cpw s0 - 2 zw s0 |
где использовано то обстоятельство, что интенсивность бегущей волны (см. формулу (4.65))
(4.97)
|
Рмс. 4.29. |
зависит не только от амплитуды s0 и частоты w, но и пропорциональна акустическому сопротивлению z. Следует отметить, что формулы (4.96) справедливы и для поперечных колебаний.
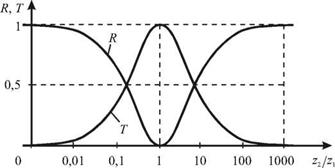
Из рисунка 4.29, на котором изображены зависимости (4.96), видно, что если z1 - z2 , отражения не происходит. Поэтому на практике, когда надо уменьшить отражение, стараются согласовать (сделать практически одинаковыми) волновые сопротивления двух сред.
Заметим также, что при z2 << z1, как в случае свободного конца стержня (z2 — сопротивление воздуха), или z2 >> z1 (закрепленный конец), R » 1,т. е. происходит практически полное отражение волны, что мы и использовали выше при рассмотрении отражения в этих предельных случаях.

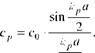
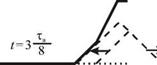

 Опубликовано в
Опубликовано в