Конические зубчатые передачи
 1 февраля, 2013
1 февраля, 2013  admin
admin Общие сведения и характеристика. Конические зубчатые колеса применяют в передачах, у которых оси валов пересекаются под некоторым углом Е (рис. 8.29 и 8.30). Наиболее распространены передачи с углом Е=90°.
Конические передачи сложнее цилиндрических в изготовлении и монтаже. Для нарезания конических колес требуются специальные станки и специальный инструмент. Кроме допусков на размеры зубьев здесь необходимо выдерживать допуски на углы Z, и 62, а при монтаже обеспечивать совпадение вершин конусов. Выполнить коническое зацепление с той же степенью точности, что и цилиндрическое, значительно труднее. Пересечение осей валов затрудняет размещение опор. Одно из конических колес, как правило, располагают консольно. При этом увеличивается неравномерность распределения нагрузки по длине зуба (см. рис. 8.13, в). В коническом зацеплении действуют осевые силы, наличие которых усложняет конструкцию опор. Все это приводит к тому, что, по опытным данным, нагрузочная способность конической прямозубой передачи составляет лишь около 0,85 цилиндрической. Несмотря на отмеченные недостатки, конические передачи имеют широкое применение, поскольку по условиям компоновки механизмов иногда необходимо располагать валы под углом.
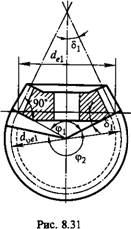
Геометрические параметры. Аналогами начальных и делительных цилиндров цилиндрических передач в конических передачах являются начальные и делительные конусы с углами Si и 62. При коэффициентах смещения инструмента хх+х2=0 начальные и делительные конусы совпадают. Этот наиболее распространенный вариант рассматривается ниже. Конусы, образующие которых перпендикулярны образующим делительных конусов (см. рис. 8.31), называют дополнительными конусами. Сечение зубьев дополнительным конусом называют торцовым сечением. Различают внешнее, внутреннее и среднее торцовые сечения. Размеры, относящиеся к внешнему торцовому сечению, сопровождают индексом е, например Re и др. Размеры в среднем сечении сопровождают индексом т: <4, Rm и др.; Re ъ Rm — Внешнее и среднее конусные расстояния, Ъ — ширина зубчатого венца.
|
(8.35) |
Размеры по внешнему торцу удобнее для измерения, их указывают на чертежах. Размеры в среднем сечении используют при силовых расчетах. Зависимости размеров в среднем и торцовом сечениях:
Re=Rm + 0,5b, de= dmRJRm, rnte=rntmRe/Rm
Для прямозубых передач торцовое T и нормальное п сечения со-
Fj
|
Рис. 8.29 |
>Fn
|
|
Впадают. При этом Mte—Mne округляют до стандартного (см. табл. 8.1[21]).
Передаточное число. Как и у цилиндрических передач,
U = D2/Dl=Z2/Zi.
Кроме того, выразив Dx и D2 через конусное расстояние R и углы делительных конусов <5i и <52, получим
U=SinS2/SinSl |
И при Е = <51+<52 = 90о w=tg52=ctg5i. j
(8.36)
Формулы (8.36) используют для определения углов <5i и 62.
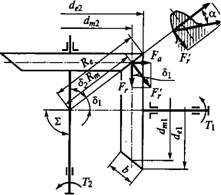
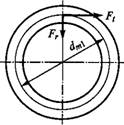
Силы в зацеплении прямозубой конической передачи. В зацеплении конической передачи действуют силы: окружная Ft, радиальная F, и осевая Fa. Зависимость между этими силами нетрудно установить с помощью рис. 8.30, где силы изображены приложенными к шестерне.
По нормали к зубу действует сила Fm которую раскладывают на Ft и F'R. В свою очередь, F'R раскладывается на Fa и Fr. Здесь
F„=Ft/Cosot, Iv'=^Tga, Fr=F'R Cos Si = Ft Tga Cos^, Fa=Ff Sin^ = Ft Tga Sin<51.
|
|
|
(8.37) |
Для колеса направление сил противоположно. При этом Fa — Радиальная сила, а Fr — осевая.
|
(8.38) |
Приведение прямозубого конического колеса к эквивалентному прямозубому цилиндрическому. Параметры эквивалентных колес используют при расчетах на прочность. Форма зуба конического колеса в нормальном сечении дополнительным конусом (рi (рис. 8.31) такая же, как у цилиндрического прямозубого колеса. Эквивалентное цилиндрическое колесо получим как развертку дополнительного конуса, которая ограничена углом <р2. Диаметры эквивалентных колес
Dye 1 = deijcos Su = ^й/COS S2.
Выражая диаметры через z и т, запишем zvlm<?=z1m<?/cos S{ или числа зубьев эквивалентных колес
|
(8.39) |
|
2* |
^vi =2'1/cos <5Ь zv2=z2/cos <5:
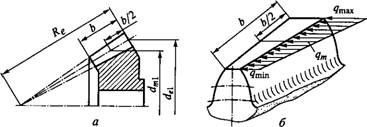
Расчет зубьев прямозубой конической передачи по напряжениям изгиба. Размеры поперечных сечений зуба конического колеса изменяются пропорционально расстоянию этих сечений от вершины конуса (рис. 8.32, а). Все поперечные сечения зуба геометрически подобны. При этом удельная нагрузка Q распределяется неравномерно по длине зуба. Она изменяется в зависимости от деформации и жесткости зуба в различных сечениях. Можно доказать, что нагрузка распределяется по закону треугольника, вершина которого совпадает с вершиной делительного конуса, и что напряжения изгиба одинаковы по всей длине зуба.
При геометрическом подобии зубьев в различных сечениях их жесткость, как консольных балок, постоянна по всей ширине колеса. Для оценки деформации положим, что зубья колеса 2 абсолютно жесткие, а зубья колеса 1 податливые. При заторможенном колесе 2 нагруженное колесо 1 повернется на угол Aq> вследствие податливости зубьев. Прогиб зубьев в различных сечениях равен RAq>, где г — радиус в соответствующем сечении. При постоянной жесткости нагрузка пропорциональна деформациям или в нашем случае радиусам г, которые, в свою очередь, пропорциональны расстояниям от вершины делительного конуса (рис. 8.32, б). Если модуль зубьев и нагрузка изменяются одинаково, то напряжения изгиба остаются постоянными [см. формулу (8.19)] по всей длине зуба.
Это позволяет вести расчет по любому из сечений. На практике за расчетное сечение принято среднее сечение зуба с нагрузкой Qm.
|
|
По аналогии с прямозубой цилиндрической передачей [формула (8.19)] запишем
AF= Y^KrKOtbmn)^?], (8.40)
Где для прямозубой передачи 0^«О,85— опытный коэффициент, характеризующий понижение прочности конической прямозубой передачи по сравнению с цилиндрической (см. с. 157), т^ — модуль в среднем нормальном сечении зуба.
Коэффициент формы зуба YFS определяют по графику рис. 8.20 в соответствии с эквивалентным числом зубьев Zv [см. формулу (8.39)]. Коэффициент нагрузки KF см. ниже.
|
/ cos<$2 (COS 8i+------------ 1. |
Расчет зубьев прямозубой конической передачи по контактным напряжениям. Для конического зацепления Рщ, в формуле (8.7) определяют по диаметрам эквивалентных колес. Согласно формулам (8.38), для среднего сечения зуба получим
1 1^1 2cOS<$! ^2Cos<52 Рпр Pi Pi 4nisina Dm 2Sina ^nisina^
Учитывая связь тригонометрических функций и формулу (8.36), находим
Я 1 1 я 1 "
Cos д2 = = ; cos<5i=-
VV<$2+1 VW1 л/tg^i + l
После подстановки и несложных преобразований запишем
±= (8.41)
Рпр Dmi Sma и J
На основании формулы (8.41) можно отметить, что приведенный радиус кривизны в различных сечениях зуба конического колеса изменяется пропорционально диаметрам этих сечений или расстоянию от вершины начального конуса. Ранее было сказано, что удельная нагрузка Q также пропорциональна этим расстояниям. Следовательно, отношение QjpЩ, постоянно для всех сечений зуба. При этом постоянными остаются и контактные напряжения по всей длине зуба, что позволяет производить расчет по любому сечению (в данном случае по среднему). Удельная нагрузка в этом сечении (рис 8.32)
Ят = (?тах + ?шш)/2 = FtKH/(B COSa). (8.42)
Сравнивая формулы (8.41) и (8.42) с аналогичными формулами (8.8) и (8.9) для прямозубых цилиндрических передач, отмечаем, что
11-7074 161
формулы для Q совпадают, а для 1 рщ различаются только числителями: у/и2+1 вместо (и-1-1). Учитывая это различие, переписываем формулу (8.10) для проверочного расчета прямозубых конических передач в виде
Где 0#=О,85— опытный коэффициент (см. ранее о коэффициенте 0F).
Для проектного расчета формулу (8.43) преобразуют. При этом учитывают, что основными габаритными размерами для конических передач являются De2 и Re, а нагрузка характеризуется моментом Т2 на ведомом валу. Вводят эти параметры в формулу (8.43) и после преобразований получают
Ге^Г (844
Где Kbe=blRe — коэффициент ширины зубчатого венца относительно внешнего конусного расстояния. Рекомендуют КЬе^0,3. Меньшие величины для неприрабатывающихся зубьев (Нх и #2>350 НВ и v>15 м/с).
Наиболее распространено ^=0,285. При этом
4а» 2,9 УЕ^иКн^вн^н}2). (8.45)
В формулах (8.44) и (8.45) принято: а = 20°, £#„«1,15 (см. табл. 8.3), (1— 0,5/^)2« 1,03(1— Кье). При выводе формул учтены геометрические зависимости:
4*1 =DM2Lu=DE2Rml(Reu)=De2 (Re—Q,5B)/(Reu)=De2 (1-0,5^)/W;
T = T2/U;
B = KbeRt=KbASdeilcos Si = (KbeOMl л/и2 +1 )/U.
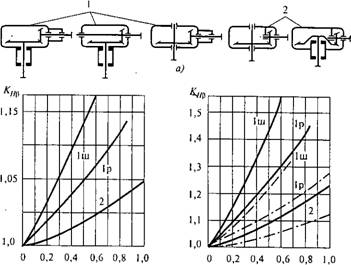
Коэффициенты расчетной нагрузки KH=KHvKHp и KF=KFvKFh где KHv и KFv определяют по табл. 8.3, при этом для прямозубой передачи точность условно понижают на одну степень против фактической, а для передач с круговым зубом — как для косозубой цилиндрической передачи той же степени точности. Кщ — по графикам рис. 8.33 [20]. На рис. 8.33 номера кривых соответствуют схемам передач (рис. 8.33, а), 1ш — шариковые, 1р — роликовые опоры; рис. 8.33, б — при твердости рабочих поверхностей зубьев
|
Khe u/( 2 - Khe) Kbe u/{ 2 ~Khe) Б) в) Рис. 8.33 |
Хотя бы у одного из колес пары Ж 350 НВ; рис. 8.33, в — при Н и #2 >350 НВ; сплошные линии для прямозубых передач, штрих - пунктирные для передач с круговыми зубьями (для этих передач при #2^350 НВ принимают Кщ= 1).
KFp=L + L,5(KHp—l) — эта формула учитывает более благоприятное влияние приработки на контактную прочность, чем на изгиб - ную, и более тяжелые последствия поломки зубьев [20].
Методика определения модуля, числа зубьев и других исполнительных размеров передачи аналогична методике определения этих параметров для цилиндрических колес (см. также пример расчета).


 Опубликовано в
Опубликовано в