Показано, что закономерности распределения коротких воло­кон в матрице могут быть описаны вероятностными соотношениями, достаточно близко характеризующими статистические характери­стики двухмерного квазиизотропного слоистого пластика.

Сделано предположение, что поле с линейным распределением! напряжений существует по всей толщине, а это совпадает с класси-1 ческой теорией слоистых пластиков.

При одноосном растяжении проявляются высокие модуль] упругости, предел прочности и относительное удлинение, в то] время как соответствующие величины при деформировании в по-] перечном направлении относительно малы. Когда слои КМ рас-1 полагаются в нескольких направлениях, итоговые механическиеj характеристики будут промежуточными между значениями, по - і лученными при продольной и поперечной деформациях. При! возрастании числа ориентированных слоев изотропная прочность достигается асимптотически. Достаточно сложения четырех одно­направленных слоев, чтобы многослойный материал при углах ориентации 0/90°/± 45° мог бы быть выбран для изотропного моделирования.

Теория максимальных напряжений, разработанная Петитом и Ваддоупсом [24], позволяет оценить прочность КМ для случая с неориентированными короткими волокнами. Первый этап в этом анализе — вычисление модуля упругости для слоевой компози­ции из связующего и коротких волокон исходя из допущения аддитивности свойств волокон и матрицы.

Продольный модуль упругости

Ea = EBVB + EMVMt (7.1)1

Где VB, VM — объемные доли соответственно волокна и матрицы.|

Поперечный модуль эластичности

Р _ Еы {1 + £,УВ [(£в/£м) - 1] [(£в/£м) + £)}

1-^в[(£в/£м)-1][(£в/£м) + а '

Где £ — коэффициент упрочнения.

Модуль упругого сдвига

Fi - Ом [ 1 + ty* (GB/GM) - 1] [(Gb/GM) + □ /7 о

12 1-^b[(GB/G„)-1][(Gb/Gm) + S] •

Основной коэффициент Пуассона

Via = vBVB + vMVM. (7.4) ■

Продольный модуль эластичности и коэффициент Пуассона] приблизительно оцениваются по «правилу смеси», которое не при­годно для расчета модуля упругого сдвига и поперечного модуля упругости. Модуль упругости волокон в значительной мере опре­деляет значение общего модуля КМ. Жесткость армирующих коротких волокон приближается к жесткости длинных волокон при их большом содержании в композитах. Прочность КМ также является функцией относительного содержания в нем волокна и с его возрастанием увеличивается до некоторого предела. В то же время она не достигает значений, характерных для КМ, арми­рованных длинными волокнами. 174

Уравнения Халпина — Кардоса [23 ] были предложены для определения фактора уменьшения прочности (ФУП). ФУП исполь­зуется для вычисления допустимых напряжений (продольного, поперечного и сдвигового) в слоистых композитах. Эти расчеты приводят к результатам, совпадающим с наблюдениями, что суще­ствует некое критическое содержание волокна в композите. Когда доля армирующей компоненты в КМ равна этому пределу или превышает его, волокно рвется, но при уменьшенной прочности композита. Ниже критического значения композит разрушается по матрице или же по поверхности раздела матрица — волокно. Эта критическая характеристика описывается соотношением

(1/<0к = (<W*m)/2,

Где ав — предел прочности при растяжении волокна; <вм — пре­дел прочности матрицы при сдвиге.

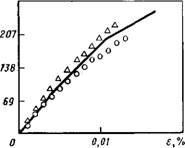
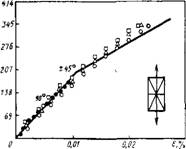
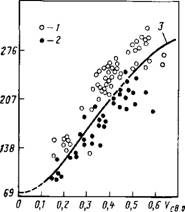
Последующие этапы моделирования осуществляются путем приложения возрастающих нагружений к многослойному мате-, риалу и изучению прочности каждого слоя на разрыв. Слои разрываются при достижении допускаемых напряжений. По мере разрыва каждого слоя, проводят пересчет модуля упругости композита на оставшееся сечение, и так продолжается вплоть до разрушения всех слоев. Результаты такого анализа продемон­стрированы на рис. 7.16 [25]. Подобные подходы для квазиизо­тропного многослойного материала с длинными волокнами иллю­стрируются данными, приведенными на рис. 7.17 [23]. На рис. 7.18 представлено сравнение теоретического и реального пределов прочности при растяжении многослойного композита с произ­вольно ориентированными в матрице короткими волокнами как функции объемной доли волокна [26].

Рис. 7.16. Зависимость напряжение а — деформация є стеклопластиков с эпок­сидным связующим, квазиизотропно-армированных короткими волокнами в со­ответствии с теорией максимальных деформаций (расчетная кривая)

Рис. 7.17. Зависимость напряжение а — деформация є сложного эпоксистекло - пластика, квазиизотропно-армированного непрерывными волокнами в соответ­ствии с теорией максимальных деформаций (расчетная кривая)

Квазиизотропный аналог сло­истого пластика приемлем не только для совершенно неориенти­рованных смесей, но может быть в равной степени использован, когда существует некоторая сте­пень анизотропии, а также для анализа систем с различной сте­пенью объемного заполнения КМ резаными волокнами. Ранее ука­зывалось, что в большинстве слу­чаев формование СВТП приводит к образованию структур, характе­ризующихся промежуточными ва­риантами расположения волокон от произвольного до анизотроп­ных. При этом длина волокна из­меняется в значительной степени. Можно ожидать, что некоторые волокна подвергнутся измельче­нию в процессе переработки до размеров ниже критического. По­следнее условие также может быть учтено при квазиизотропном ана­лизе систем. Тот факт, что упомя­нутое вышерассмотрение проводи­лось с термореактивными смолами, не должен влиять на его использование в композитах с термопластичными связующими. Необходимость дальнейшего совершенствования теории обусло­влена реальной неаддитивностью свойств, нелинейным поведе­нием связующего. Теория должна учитывать возможность более точной оценки концентрации напряжений на концах арми­рующих волокон.