Удаление жидкости из цементного геля под дейст­вием нормального давления сопровождается фильтра­ционными процессами, не получившими освещения в технической литературе. Большую роль в этом играют разность химических потенциалов взаимодействующих фаз и различные градиенты, возникающие в системе в зависимости от вида источника энергии, под влиянием которой перемещается жидкость. Так, градиент плотно­сти вызывает движение влаги из крупных пор в полости с мениском меньшего радиуса кривизны. Перемещение жидкости под действием градиента влажности происхо­дит в сторону менее увлажненных пор до полного вы­равнивания влажности. Перепад температур вызывает появление градиента упругости водяного пара, который диффузно передислоцируется в сторону более низких температур.

Следовательно, для удаления жидкости из цементно­го геля под давлением необходимо совершить работу (затратить энергию) на преодоление сил связи жидко­сти с частицами цемента и на перемещение ее в систе­ме. Естественно, что основная задача исследования ки­нетики фильтрации жидкости из цементного геля заклю­чается в определении зависимости скорости фильтрации от различных технологических параметров и величины нормального давления.

Из гидродинамики известно, что в движущемся по­токе падение давления прямо пропорционально его ско­рости. Очевидно, что при фильтрации цементного геля давление в отжимаемой жидкости также должно сни­жаться под действием внешней нормальной нагрузки, и, надо полагать, что при движении жидкости в прост­ранстве между сольватированными частицами цемента в пограничных диффузных слоях будет создаваться раз­ность давлений.

Молекулы воды в диффузных слоях испытывают дей­ствие сил, направленных к поверхности твердой фазы, которые убывают с увеличением расстояния от поверх­ности частиц. При определенной скорости фильтрации в потоке может возникнуть отрицательное давление такой величины, когда равнодействующая сил, одна из кото­рых притягивает молекулы воды к твердой поверхности, а другая втягивает ее в движущую струю, окажется на­правленной от твердой поверхности. В этом случае ори­ентированные молекулы жидкости в диффузном слое выйдут из сферы влияния сил притяжения и будут во­влечены в движущийся поток.

Подобное явление наблюдалось при изучении филь­трации в грунтах. В связи с этим в работе [133] отме­чено, что молекулы диффузного слоя могут перемещать­ся в водонасыщенных грунтах. При разности напоров свободной воды они отрываются под влиянием фильтра­ционного потока. При этом чем больше скорость филь­трационного потока, тем более существенные изменения могут вноситься в структуру молекул воды сольватных оболочек и больше молекул связанной воды может быть увлечено и вынесено движущейся струей.

В процессе течения нарушается ориентация диполей воды, а поэтому плотность и вязкость диффузных слоев жидкости, вовлеченной в фильтрационный процесс, мо­гут быть приняты такими же, как для обычной воды, например при скоростях порядка 1 мм/с вязкость очень быстро достигает нормальной величины. При этом упру­гость пара, химический потенциал и свободная энергия могут повышаться за счет работы внешних сил, затра­ченной при движении слоя жидкости, сверх той, которая рассеивается в тепло. При полной дезориентации ди - польной структуры молекул воды прежние аномальные свойства ее не могут восстанавливаться (хотя этому и соответствовало бы уменьшение химической активно­сти) из-за потенциального барьера, появление которого обусловлено приложенным внешним давлением. Барьер может быть преодолен, если первоначальная аномаль­ная структура не была до конца деформирована.

При восприятии внешней сжимающей нагрузки си­стемой нейтральных давлений в жидкости, заполняющей поры цементного геля, возникает гидростатическое дав­ление, которое сразу же передается на прилегающие частицы твердой фазы и по мере сжатия верхних слоев
цементного геля распростра­няется на нижележащие. В связи с этим гидростатичес­кое давление в жидкости (за­ключенной в порах цементно­го геля) уменьшается на вели­чину соответственно той части полного давления, которое ис­пытывают твердые частицы, расположенные на определен­ной глубине от поверхности приложения внешней нагрузки.

Обозначим давление, воспринимаемое частицами твердой фазы, через Рт, давление в жидкости — Рш. Тогда полное давление, приходящееся на цементный гель, Р=РЖ+РТ. Величины Рш и Рт переменные, они изменяются в зависимости от высоты испытуемого об­разца и продолжительности действия внешней нагрузки, а именно: Рт уменьшается, а Рш возрастает с глуби - биной распространения внешнего нормального давления, однако снижается под влиянием продолжительности его действия. Поэтому жидкость в нижних слоях испытуе­мого образца цементного геля будет находиться под большим гидростатическим давлением, чем в верхних, расположенных ближе к месту приложения нагрузки. Это обстоятельство обусловливает движение жидкости снизу вверх. Давление ее прекращается при исчезнове­нии разницы гидростатических давлений на различных уровнях. Такое равновесное состояние наступает в том случае, когда давление Р будет полностью воспри­ниматься частицами твердой фазы. Очевидно, что до этого момента пористость цементного геля будет тоже изменяться в зависимости от расположения слоев по высоте образца и продолжительности действия внешнего давления; по мере удаления, от поверхности его прило­жения она возрастает, а с увеличением времени дейст­вия сжимающей нагрузки уменьшается.

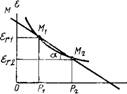
Предположим, что на рис. 3.13 изображена компрес­сионная кривая цементного геля; для отрезка ее между точками Mi(eri, Pi) и М2(ег2, Р2), заменив кривую хор­дой, можно написать соотношение [100]:

— tg а = (врд - еГ)2)/(Рх - Р2), (3.41)

Решая уравнение относительно еГ2, получим

Рис. 3.13. Элемент ком­прессионной кривой це­ментного геля

8г,2 = eP? i + tg а (Рх - Р2). (3.42)

Полагая, что еГ2 и Р2 являются частными значениями переменных ег и Р, уравнение (3.42) можно преобразо­вать:

Ег — В — tg а Р.

Дифференцируя это выражение по dP и обозначив tga =a0, получим

Der = — a0P. (3.43)

Предположим, что dPT/dt выражает возрастание за вре­мя t давления Рт, воспринимаемого частицами твердой фазы на глубине х от поверхности приложения внешней нагрузки. В этом случае, согласно (3.42), приращение количества жидкости q, которое из слоя, расположенно­го на уровне х, за время t отожмется через единицу по­верхности, будет равно

Q — — а0 dP.

Величину а0, характеризующую изменение пористо­сти цементного геля под действием нормального давле­ния, назовем сжимаемостью или коэффициентом уплот­нения цементного геля, который, согласно (3.41), может быть выражен в виде

Ао = (еР, о-е1)/(Р-Р0). (3.44)

Общий массовый расход фильтрата Q определится из выражения:

С dPr

Q==a°)~d^dX' (3'45) я

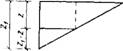
Если учесть, что давление Р слагается из суммы Рт+ и принять, что распределение давления при неко­тором допущении подчиняется закону гидростатики, то можно составить пропорцию (рис. 3.14):

Pm/P = (x1-x)/xlt

Откуда

Pm = P(-x/xj. (3.46)

Внося (3.46) в выражение (3.45) и взяв частную про­изводную по t, получим

DPJdt = Р [x/xfj (dxjdt). (3.47)

Поскольку

Разность давлении Р—Рт—Рук определяет напор, под действием которого жидкость с глубины

Х вытесняется к поверхности испытуемого образца, а Кф — среднее значение коэффициента фильтрации, тогда

Р = [W*- (3.48)

Аф J

Ф О

Подставив в (3.48) значения для Q и dPTjdt из (3.45) и (3.47) при х=0, будем иметь

Xt Хх

D До Рш С, С D * Dx

О х 1

После взятия тройного интеграла получим

= 2,45 У(Кф^/(а0 рж). (3.49)

Подставив полученное значение для Х в уравнение (3.46), определим

Введем коэффициент Сщ=Кф! {а0рж), характеризую­щий скорость уплотнения цементного геля; при рш= = 0,001 кг/см3. Тогда окончательно будем иметь

PT = p(l —0,0127 *"|Л/(Ску t) ), (3.50)

Где Рж = 0,0127 *lA/(CKy0 .

Пользуясь формулой (3.50), можно приближенно вычислить ту долю внешнего давления, приложенного к цементному гелю, которая по истечении времени T на глубине х передается частицам твердой фазы. Уравне­ние (3.50) имеет физический смысл до восприятия дав­ления слоем цементного геля, соприкасающимся с дном пресс-формы. С этого момента возможность применения зависимости (3.50) определяется критерием, получен­ным при подстановке в (3.49) Х — Hy т. е.

____ У Рис. 3.14. Соотношение между [ Рт и Рж

* = 0,00017 («о №)/Кф. (3.51)

Из формулы (3.50) следует, что при соблюдении ус­ловия (3.51) давление, приходящееся на твердую фа­зу, убывает с расстоянием от поверхности его приложе­ния, что согласуется с формулой (3.33), а гидростатиче­ское давление в жидкости, заполняющей поровое пространство в цементном геле, наоборот, возрастает. Расчеты показывают, что время t, в течение которого внешнее давление в цементном геле передается части­цам твердой фазы, зависит от объема жидкости, напол­няющей поровое пространство; чем больше х при дан­ном Л, тем дольше перераспределяется давление и по мере его восприятия твердой фазой гидростатическое давление снижается и вместе с этим замедляется ско­рость отжатия жидкости из цементного геля.

Исследование кинетики отжатия жидкости из цемент­ного геля под влиянием ступенчато приложенного нор­мального давления проводили, измеряя скорость филь­трации жидкости и изменение электрического сопротив­ления цементного геля в процессе деформации сжатия[5]. В опытах использовали разъемную стальную цилиндри­ческую форму, в которой для электроизоляции испы­туемого объекта от металла его помещали в разъемный цилиндр из органического стекла с внутренним диамет­ром 80 мм. Давление на цементный гель, помещенный в упомянутый цилиндр, передавали от 50-тонного гидрав­лического пресса через стальной поршень с уплотни - тельным кольцом, вода отжималась через перфориро­ванное днище рабочей камеры с коническим поддоном для стока жидкости. С наклонного днища поддона вода стекала через резиновую трубку в мензурку, по делени­ям которой непрерывно измеряли объем жидкости, от­жатой из цементного геля. Чтобы предотвратить выдав­ливание цементного геля через перфорированное дни­ще, на него укладывали бумажные фильтры.

161

Одновременно с объемом отжатой жидкости измеря­ли линейную деформацию и электрическое сопротивле­ние образца в период уплотнения. Стальные электроды были вмонтированы в стенку цилиндра из оргстекла и не препятствовали равномерному сжатию цементного геля под давлением. Количество отжатой жидкости и деформацию цементного геля замеряли через каждые
5 с на стадии интенсивной фильтрации и в процессе ее затухания с интервалами 15 с. Объем отжатой жидко­сти контролировали, взвешивая образец (в форме) пос­ле прессования.

Рассмотрим результаты экспериментальных исследо­ваний процесса отжатия жидкости и деформации це­ментного геля под внешним нормальным давлением, Как было экспериментально установлено, после прило­жения внешней нагрузки из образца отжимается неко­торый объем жидкой фазы АУЖ, и система деформиру­ется на величину АЛ. В начале отжимается «свобод­ная» жидкость из нижних слоев образца и для удаления ее из цементного геля не требуется большого усилия, поскольку внутреннее сопротивление сравнительно неве­лико. В этом случае реактивный отпор цементного геля на этой стадии уплотнения незначителен и стрелка на манометре пресса не фиксирует повышение давления. Отжатие жидкости из нижней части образца сопровож­дается уплотнением цементного геля; в этих его слоях образуются направленные фильтрационные каналы, по которым под действием нормального давления (система нейтральных давлений) фильтруется «свободная» жид­кость из расположенных выше слоев. Этот процесс со­провождается деформацией цементного геля по всей вы­соте образца до сближения сольватированных частиц.

К определенному моменту из образца отжимается ос­новная часть «свободной» жидкости (некоторое ее ко­личество остается защемленной в структурных порах це­ментного геля) и вместе с замедлением фильтрации жидкости уменьшается скорость изменения деформации цементного геля (рис. 3.15). Теперь внешнее давление начинает восприниматься сольватированными частица­ми цемента и преобладающей становится система эф­фективного давления; возникает значительный реактив­ный отпор движению поршня и стрелка манометра фик­сирует увеличение давления. Если внешнее давление оказывается достаточно высоким, тогда объем образца незначительно изменяется.

Во время уплотнения цементного геля наблюдаются синхронное изменение количества жидкости в нем и де­формации образцов (рис. 3.15): в начале отжатия жид­кости значения AVVAt и Д/г/Д/ резко возрастают и, до­стигнув максимальных величин, снижаются и постепенно уменьшаются. Это свидетельствует о прекращении филь­трации и установлении равновесного состояния между внешним и внутренним сопротивлением. Другими слова­ми, после отжатия из цементного геля «свободной» жид­кости гидростатическое давление воспринимается си­стемой эффективных давлений; внутреннее сопротивле­ние быстро возрастает по мере увеличения внешнего давления, что фиксируется по показаниям манометра пресса. При этом максимумы интенсивности отжатия жидкости и деформации, а также точка перелома кри­вой электрического сопротивления цементного геля сов­падают во времени.

Отсюда можно заключить, что между давлением иво - досодержанием в каждый период времени развития ком­прессионного процесса существует полное соответствие. Следовательно, пористость цементного геля, рассчитан­ная по приведенным ранее зависимостям, изменяется в объеме образца неравномерно из-за неодновременного вовлечения отдельных слоев цементного геля в процесс уплотнения под воздействием внешнего нормального давления.

При небольших давлениях вначале пористость це­ментного геля изменяется несущественно. Затем проис­ходит значительная деформация сжатия системы. При этом степень относительного уплотнения пропорциональ­на давлению и начальному водосодержанию. По абсо­лютной величине плотность цементного геля на каждой стадии уплотнения обратно пропорциональна (В/Ц)иач.

Вслед за снижением интенсивности фильтрации ста­билизируется и пористость цементного геля. При этом соответствующее время также пропорционально прессу­ющему давлению. В дальнейшем фильтрация жидкости происходит при установившейся пористости цементного геля.

Для указанного случая среднюю скорость движения жидкости при отжиме ее под давлением из цементного геля можно вычислить по формуле, приведенной в рабо­те [79]:

<n2djД р

Wcv-C°(l-mf3 Iih ' (3'52)

Поскольку при некоторой минимальной пористости mmin цементного геля, соответствующей предельному значению коэффициента пористости ег, фильтрации жид­кости не происходит, формулу (3.52) можно предста­вить в виде

2

(m0CT — mmin)2 <[6]ЦР (1_тост)2/3 ^ •

Для частиц угловатой формы принимают С0=6. По­лагая, что (1—тост)2/3 мало отличается от (1—тост), будем иметь

W = 6 ^m°CT mmin) <Р

1 — m0CT [ih

Где т0Ст —остаточная пористость цементного геля при данном нор­мальном давлении Р йц — средний диаметр частиц твердой фазы; H — толщина фильтрующего слоя (образца) цементного геля.

Коль скоро под влиянием давления Р из цементного геля отжимается «свободная» жидкость, можно принять [а=0,01 г-с/см2*. Средний диаметр частиц твердой фа­зы, определенный по способу, изложенному в работе [7], равен примерно 0,0023 см. В экспериментах толщи­на образца составляла H= 15 см. Подставляя эти значе­ния в (3.53), получим частное выражение для скорости фильтрации:

Гср = 0,21 р. (3.54)

При стабилизации процесса фильтрации №ср может быть вычислено по зависимости

Wcp = Q/SB. (3.55)

Где Q — установившийся объемный расход жидкости; S3 — площадь сечения эффективных (фильтрующих) поровых каналов.

Так как Q = kVm/ht, получим

1ГСр = АКж/(5эА0. (3.56)

Если гпост — остаточная пористость при данном зна­чении X, тогда площадь сечения 5Э эффективных пор в испытываемом образце цементного геля цилиндрической формы радиуса г0б может быть определена по зависи­мости

5э = тостЯЛоб - (З-57)

Поскольку т0ст=8г/(1+8г), где ег — остаточный ко­эффициент пористости при данном нормальном давле­нии Р, получим

При внутреннем радиусе пресс-формы г06=4 см фор­мула (3.58) преобразуется следующим образом:

№ср = 0,02(1 + ег)/егАУж/А/. (3.59)

Сопоставляя (3.54) и (3.59), можно заметить, что при каждом нормальном давлении Р скорость фильтрации определяется остаточной пористостью цементного геля и объемным расходом'жидкости.

Скорость приложения и продолжительность действия внешнего давления определенным образом влияют на скорость фильтрации жидкости из цементного геля. Со­гласно табл. 3.4, продолжительность действия нагрузки в диапазоне 15—300 с при каждой скорости ее прило­жения способствует увеличению скорости фильтрации. Однако уже с 225 до 300 с увеличение скорости при­ложения давления не сказывается на изменении объема фильтрата. Аналогичным образом это проявляется и на объемной деформации цементного геля.

ТАБЛИЦА 3.4. ВЛИЯНИЕ СКОРОСТИ ПРИЛОЖЕНИЯ НОРМАЛЬНОГО ДАВЛЕНИЯ НА КИНЕТИКУ ОТЖАТИЯ ЖИДКОСТИ И ДЕФОРМАЦИЮ ОБЪЕМА ЦЕМЕНТНОГО ГЕЛЯ ПРИ (К нг =0,295) И Р-3 МПа Скорость приложения давления, мм/мин Продолжительность"приложения давления, с И Св В S ^ Tr Средняя мак­симальная скорость фильтрации Wax, см/с Средняя ко­нечная де­формация, мм Среднее ко­личество от­жатой жид­кости за 300с, мл © « 15 30 60 80 150 225 300 10 0 4 14,5 9,5 32 55 • 68 71 0,110 0,118 20 76 0,233 0,5 5 13,5 18 19 20 10 5,5 17 33 53 73 81 0,127 1 4,5 9 12 15,5 19 20 20 2 11 17 36 61 73 74 0,140 0,132 20,2 74,5 0,235 2 6 13 16 21 23 23 4 16 31 48 66 73 75 0,123 5 8,5 11,5 14 16,5 17,5 17,5 60 15 28 40 47 61 68 71 0,156 0,176 18,8 75 0,243 8,5 11 13 15 16,5 17,5 17,5 11 21 35 48 65 72 75 0,183 8,5 10 13 15 18,5 19 19 16 23,5 37 48 65 76 79 0,188 9 10,5 13 15 18 20 20

Примечание. Над чертой — количество отжатой жидкости; под чертой — абсолютная деформация сжатия.

При данных значениях X и величинах Р максималь­ная скорость фильтрации прямо пропорциональна скоро­сти нагружения и чем она выше, тем раньше достигает­ся Wmax, так как быстрее возрастает гидростатическое давление в цементном геле, под влиянием которого от­жимается жидкость. Однако следует заметить, что с уве­личением скорости нагружения общее количество от­жатой жидкости и величина полной объемной деформа­ции цементного геля несколько снижаются, так как при быстром (почти мгновенном) приложении давления жид­кость защемляется в микрокапиллярах и фильтрация замедляется. Отсюда можно заключить, что скорость приложения внешнего давления и продолжительность ее действия зависят от начального содержания воды в це­ментном геле, т. е. значения X, и существенно влияют на

ТАБЛИЦА 3.5. ВЛИЯНИЕ (В/Ц) £ач и ПРЕССУЮЩЕГО ДАВЛЕНИЯ НА (В/Ц) JCT И СКОРОСТЬ ФИЛЬТРАЦИИ (В/Ц)нач « <и S О) Я" I О « . я 03 Н Н Ы О Н § WGV по фор - муле Ё £ CU О л 03 - СЗ А О Я г A S <L) fs О н^ Ен KJ О В (3.59). (3.54) 0,876Кн. г— =0,258 1 2 3 4 5 6 1,340 1,345 1,3 1 1.349 1.350 1,348 0,347 0,346 0,349 0,348 0,348 0,347 46 66 73 81,5 88 92 0,224 0,208 0,198 0,191 0,186 0,184 0,269 0,254 0,246 0,238 0,233 0,232 0,067 0,113 0,168 0,216 0,239 0,253 0,069 0,109 0,144 0,176 0,210 0,227 1 КН, г= =0,295 1 2 3 4 5 6 1,300 1,284 1,295 1,283 1,294 1,290 0,384 0,378 0,382 0,379 0,382 0,380 72 93 108 112 118 128 0,242 0,220 0,209 0,207 0,204 0,194 0,293 0,274 0,266 0,265 0,263 0,253 0,121 0,214 0,277 0,309 0,315 0,320 0,092 0,149 0,208 0,253 0,296 0,312 1,3 /Сн, Г= =0,384 1 2 3 4 5 6 1,148 1.150 1,155 1,152 1,143 1.151 0,440 0,442 0,442 0,441 0,440 0,441 130 164 172 184 186 191 0,270 0,242 0,233 0,223 0,221 0,217 0,339 0,312 0,308 0,299 0,296 0,293 0,156 0,249 0,309 0,312 0,346 0,340 0,157 0,242 0,332 0,398 0,476 0,55

Скорость фильтрации. Однако на общем количестве от­жимаемой жидкости и полной деформации цементного геля (достигаемое уплотнение) скорость приложения давления не сказывается. Кроме того, в экспериментах было замечено, что скорость фильтрации не зависит от объема испытываемого образца; при X в интервале 0,876—1,3, давлении до 8 МПа и различных интенсив - ностях нагружения фильтрационные закономерности описываются однотипными кривыми.

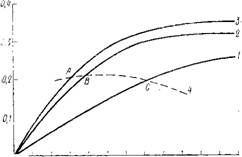
Средние скорости фильтрации, вычисленные по фор­мулам (3.54) и (3.59) для трех значений: Х=0,876; 1,0 и 1,3 при нормальных давлениях Р от 1 до 6 МПа, при­ведены в табл. 3.5. Если изобразить полученные значе­ния WCp графически, можно заметить, что до точек Л, В и С функция WCp=Fo(P) выражается прямыми, кото­рые затем переходят в кривые экспоненциального вида (рис. 3.16). Сопоставление вычисленных по формулам (3.54) и (3.59) значений WcР показывает, что до ука­занных характерных точек они практически совпадают, а при нормальных давлениях, превышающих соответст­вующие точкам А, В к С значения, формула (3.54) дает сильно расходящиеся результаты. Объясняется это тем, что формула (3.54) выведена для условий с равномер­ным ламинарным режимом фильтрации жидкости через поровые каналы, поэтому по ней получаются данные, вполне применимые при прямолинейной закономерно­сти фильтрации, соответствующей именно ламинарному характеру движения жидкости.

Рис. 3.16. Характер

Wrp, сц'с

0 0,5 1 If 2 2,5 J 5t5 4 4,5 5 5,5 Р,ППа

Изменения кривых скоростей фильтра­ции жидкости при прессовании це­ментного геля

1, 2 и 3 — при X, Равных 0,876; 1 и 1,3 соответственно; 4 — Кривая, ограничива­ющая область лами­нарной фильтрации

Формула (3.59) хотя и основана на законе Дарси, однако отношение AVm/At учитывает специфические осо­
бенности фильтрации жидкости, связанные как с измене­нием строения поровых каналов, так и с переходом ла­минарного движения в турбулентное при определенных величинах внешнего нормального давления. Возникнове­ние турбулентного, или лучше сказать квазитурбулент­ного, режима фильтрации по всей вероятности должно сопровождаться локальными завихрениями линий тока при огибании частиц твердой фазы и преодолении дру­гих препятствий. При «турбулентном» режиме происхо­дит редеформация молекул жидкости в диффузных сло­ях и вовлечение их в процесс фильтрации. Далее в «турбулентном» потоке во взвешенном состоянии могут находиться высокодисперсные фракции твердой фазы, отжимаемые частично вместе с жидкостью из цементно­го геля, что, кстати, обычно наблюдается при его уплот­нении под давлением.

Критическая скорость фильтрации WKVf при которой может возникнуть турбулентное движение жидкости в поровых каналах цементного геля, определяется крите­риальным числом Рейнольдса — Re.

Если dK— средний диаметр поровых каналов в це­ментном геле и v — кинематическая вязкость жидкости, равная (ig)lp™> см2/с, то безразмерный критерий Re бу­дет иметь вид

Re = (WKpdH)/v. (3.60)

Для того чтобы вычислить значения Re, необходимо определить dK при соответствующих Р или WKP. Под действием внешнего давления жидкость фильтруется од­новременно не из всех пор; в первую очередь в этот процесс включаются слои цементного геля, непосредст­венно воспринимающие давление, и по мере его перерас­пределения вовлекаются остальные слои, более удален­ные от места приложения нагрузки. При повышении внутреннего гидростатического давления жидкость уст­ремляется из микропор к более крупным порам, созда­ется как бы поток, который пробивает себе путь по крат­чайшему направлению — протоку, ориентированному вдоль действия силового поля [7].

Такой поровой канал весьма сложного строения мо­жно заменить каналом цилиндрической формы, площадь поперечного сечения которого равна площади попереч­ного сечения действительного порового канала в его са­мом узком месте, а длина порового канала равна тол­
щине испытуемого образца [79]. Так как элементарные струйки жидкости движутся между шарообразными части­цами фиктивного грунта, огибая их, то траектория течения частиц жидкости бу­дет выражаться некоторой криволиней­ной в пространстве линией. Из совокуп­ности этих линий потока составляется элементарная струйка, протекающая че­рез пору. При этом осью струйки будет служить кривая АКВНС (рис. 3.17).

Согласно [79], средняя по длине струйки площадь сечения равна

Ат = 0,2118 4. (3.61)

Исходя из предположения, что в углах порового ка­нала образуются «мертвые зоны» с застойной жидко­стью, Слихтер принимает эффективную площадь сече­ния равной

Л3 = 0,14754, (3.62)

Где гш — радиус шаров, составляющих модель фиктивного грунта. Сопоставляя (3.61) и (3.62), получим

1,436, (3.63)

Ав

Откуда Ат = 1,436ЛЭ.

Таким образом, при теснейшем расположении ша­ров (0=60°) действительный поровой канал АКВНС может быть заменен прямолинейным каналом Л С, пло­щадь поперечного сечения которого выражается зависи­мостью (3.63). Из геометрических построений следует, что длина I прямолинейного канала, эквивалентная дли­не криволинейного канала, равна

/=L,065/I. (3.64)

При равномерном ламинарном течении жидкости по цилиндрической трубе средняя скорость потока выража­ется формулой __

WCv = (AmP)/{20IilV З). (3.65)

Внося в (3.65) значения Ат и /, а также определив, что (1,065 • 20 • J/3) /1,436—8я, будем иметь

Wcv = (AdP)/(8wh). (3.66)

В таком случае на основании (3.56) и (3.57) можно написать:

(А^ж)/КбАКст) = {лэр)тлн), Отсюда Аэ будет равно:

Л9 = (8рШж)/{т^ Г20б РМ). (3.67)

Для цилиндрического порового канала Ad=nr2Ki тогда по формуле (3.67) будем иметь

' (3.68)

^ост^об РМ

Где H — толщина образца в направлении фильтрации, где происхо­дит перепад гидростатического давления.

440 V

Применительно к условиям экспериментов имеем: H= 15 см, А/=50 с, г0б=4 см и [л=0,01 П[7]. Подставляя эти значения в (3.68), получим следующую расчетную зависимость:

Д1/ж

./ —— • (3.69)

1440 V т0СТР V '

Радиусы поровых каналов, вычисленные по формуле (3.69), приведены в табл. 3.6. Пользуясь ею и рис. 3.16,

(3.70)

Нетрудно определить диаметры поровых каналов, соот­ветствующие WKР для каждого значения х цементного геля, а именно: при Х=0,876—dK=10,4 мкм; X=l—DK= = 16 мкм и Х= 1,3—dK= 19,2 мкм. Подставляя эти зна­чения DK в формулу (3.60), получим частные ее выраже­ния для указанных значений X:

Re0,876 = 0.Ю4 №кр; Re^O. l 6ГКР; Re1>3 = 0,192 Гкр.

Согласно рис. 3.16, критические скорости фильтрации, определяемые точками пересечения кривой ABC с кри­выми i, 2 и 3, могут быть для всех трех значений X при­няты равными 0,2 см/с. В таком случае критерий Re при Х=,0'876; 1 и 1,3 будет иметь следующие значения: 0,028;

ТАБЛИЦА 3.6. ВЛИЯНИЕ НОРМАЛЬНОГО ДАВОЕНИЯ НА ИЗМЕНЕНИЕ СРЕДНЕГО РАДИУСА ПОРОВЫХ КАНАЛОВ В ЦЕМЕНТНОМ ГЕЛЕ Значения X Давление, МПа Приращение объема отжатой воды 6УЖ, см3 Средняя порис­тость тк в интер­вале времени 62=50 с Средний радиус поровых каналов гк мкм 0,876 1 2 3 4 5 6 2,3 3 4,3 4,9 6,1 6,3 0,269 0,254 0,246 0,238 0,233 0,232 6,5 5,5 5,35 5,1 5 4,7 1 1 2 3 4 5 6 4 7 8 10 10 10 0,293 0,278 0,266 0,265 0,263 0,253 8,2 7,9 6,9 6,8 6,15 5,8 1,3 1 2 3 4 5 6 5,5 8,3 12 13 14 14 0,339 0,315 0,308 0,299 0,296 0,293 9 8,2 8 7,45 6,8 6,3

0,032 и 0,0384 соответственно. Можно принять, что Re

Изменяется в узких пределах: от 0,03 до 0,04. __

Заметим, что при исследовании фильтрации воды че­рез песок с крупностью зерен dn=0,02 см, плотностью 2,65 и пористостью 50% экспериментально определено Re ^0,1 [45]. Такая разница в численной оценке Re впол­не реальна, так как в цементном геле диаметры поровых каналов во много раз меньше, чем в мелкозернистом пе­ске. Закономерности фильтрации жидкости из цемент­ного геля, обусловленные воздействием внешнего давле­ния, могут быть использованы при описании процессов деформации бетонной смеси, например в процессе цент­рифугирования, вакуумирования и вообще во всех тех случаях, когда уплотнение смесей сопровождается вы­теснением (отжатием) жидкости, содержащейся в це­ментном геле.