Большой интерес для практики представляет расчет дуг с изме­няющейся во времени длиной, что имеет место, в частности, во мно­гих коммутационных аппаратах. Необходимую для расчета таких дуг дифференциальную вольт-амперную характеристику можно получить следующим образом. Перепишем (7.14) в виде

ЕШМт) = ШИт) ♦ ЫЕ{Е*/Е* - 1).

эф

Если длина дуги изменяется во времени, но так, что не возникают концевые эффекты, то это уравнение остается справедливым. Обозна­чим / = и = Ei, U = Е I. Тогда дифференциальная харак-

О 0 эф О

теристика дуги с изменяющейся длиной принимает вид

du/di = (и/і )di/dr - bu(u/f - 1) + udf/dr, (7.15)

где и = и/t/g. Если задан вид функции /(г), то из совместного ре­шения (7.15) и уравнений цепи можно найти ни/.

Рассмотрим цепь с дугой и индуктивностью и примем, что длина дуги увеличивается по линейному закону / = /Q(l + kr). Уравнения

для расчета такой цепи имеют вид

du/dr = (n//)[osin (т + ф) - и] - bu[u2( 1 + kr) 2 - 1] + ku; di/dr = asin (т + ф) - и,

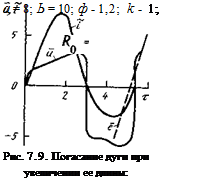
где в величины а, и, / входит I/ , а не V, как было ранее. На рис. 7.9 показаны результаты расчета такой цепи при относительно
быстром увеличении длины дуги. В течение первого после поджига полупериода напряжение на дуге быстро увеличивается, во втором полупериоде оно остается приблизительно постоянным, однако эф­фективное значение тока существенно уменьшается по сравнению с первым полупериодом. После второго перехода через нуль дуга погасает: ток прекращается, а напряжение становится равным ЭДС (штриховая кривая).

Подобным же образом можно исследовать влияние периодического изменения длины дуги на и и і (например, вследствие механизма шунтирования). Один из возможных вариантов дифференциальной вольт - амперной характеристики дуги в этом случае имеет вид

du/dr = (u/i)di/dT - bu(t?//2 - 1) + u(dl/di)(di/dT)> где К і) - заданная периодическая функция, выражающая зависимость длины дуги от силы тока.

В качестве простейшего случая можно положить

7 * М = 1 + Асов ( ~- І/І ), о < k < 1.

о :г шах

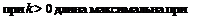При k = 0 длина дуги постоянна,

і = і и минимальна при і = 0. max

Дифференциальное уравнение (7.15) можно использовать для рас­чета восстанавливающегося напряжения. Известно, что после пога­сания дуги начинается процесс восстановления напряжения на раз­рядном промежутке, который может быть как апериодическим, так и колебательным. При колебательном процессе возможны большие пере­напряжения, опасные для электрооборудования, поэтому изучение процесса восстановления напряжения представляет большой интерес.

Вернемся к рассмотрению цепи, изображенной на рис. 7.4. Будем считать, что длина дуги увеличивается по линейному закону. Урав­нения для расчета такой цепи имеют вид

d/j/dr = asin (т + ф) - и + Ri ^

du/dr = g(і - і);

di/dr = (gi/u)(і ^ - і) - ki + bi[t?{ 1 + kr) 2- 1].

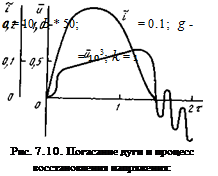
Пример расчета полученной системы уравнений показан на рис. 7.10. Видно, что в данном случае дуга погасает после первого же перехода через нуль и далее идет колебательный процесс восста­новления напряжения, обусловленный наличием в цепи даже весьма малой шунтирующей дугу емкости. Полученные дифференциальные вольт - амперные характеристики дуги могут быть использованы также для расчета переходных процессов в цепях с дугами, питающимися от ис­точников постоянного напряжения.