Истечение жидкости из пен происходит по каналам Плато — Гиббса под действием сил тялсестн и капиллярных сил всасы­вания. В пенах и вертикальных свободных пленках эти силы действуют одновременно. В горизонтальных свободных пленках влияние гравитационных сил отсутствует и процессы утончения н разрушения таких пленок происходят под действием только капиллярных сил, которые, как показано ранее (см. гл. 3), за­висят от кривизны канала и центрального участка пленкн.

Гравитационные силы регулируют истечение жидкости через нею сеть каналов Плато, но оказывают пренебрежимо малое влияние на переток жидкости нз пленок к этим каналам, кото­рый обусловлен, главным образом, капиллярными силами и не зависит от ориентации пленки. Это подтверждает простой рас­чет. Если принять длину капилляра I равной 0,05 см, то макси­мальное давление вследствие истечения жидкости под дейст­вием гравитационных сил из пленок к каналам Плато составит Aprp=pg/«5 Н/м2. Радиус кривизны г канала Плато всегда меньше длины канала. Допустив, что г = 0,5/, получим значение давления вследствие капиллярных сил Арк = а/г — 120 Н/м2 при о=0,03 Н/м.

Поведение жидкости в пене, находящейся в гравитационном поле, определяется соотношением между капиллярными силами и силой тяжести, выраженным в виде условия гидростатическо­го равновесия (3.1). На первой стадии после образования пены преобладают капиллярные силы (рG<—dpjdh), под действием которых происходит перетекание жидкости из пленок в каналы Плато — Гиббса. Такое перераспределение жидкой фазы внеш-

П,I

64

Не выражается в «задержке» истечения жидкости, которая в работе [110] названа периодом накопления. Этот период харак­теризуется интенсивным укрупнением пузырьков в результате диффузии газа и расширением каналов Плато — Гиббса. Пе­риод «задержки» включает также время, необходимое для на­копления жидкости в нижнем сечении пенного столба. Продол­жительность «задержки» увеличивается с ростом кратности пены и уменьшается (до критического значения) с увеличением се

Столба.

Истечение жидкости начинается при условии pg>—Dpjdh и состоит из стадии ускорения истечения и синерезиса, протекаю­щего с постоянной скоростью. По мере истечения жидкости возникает и возрастает градиент капиллярного давления по вы­соте столба, препятствующий дальнейшему вытеканию жидко­сти. Скорость вытекания непрерывно уменьшается вплоть до

Полного разрушения пены.

Типичные кривые истечения жидкости нз иен, полученных

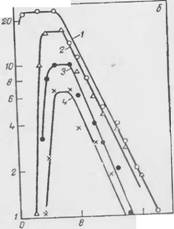
Методом барботпроваиия воздуха через растворы сульфонола НП-1, иллюстрирует рис. 30. Как видно по кривым па рис. 30, а, уже при концентрации сульфонола в растворе 0,5% наблюдает­ся некоторая задержка истечения, продолжительность которой возрастает с ростом концентрации ПАВ. Кривые на рис. 30,6 показывают, что истечение жидкости (от начала процесса) про­исходит в три этапа: вначале скорость увеличивается до некото­рого максимального значения, затем она остается некоторое время постоянной и, наконец довольно быстро снижается. Наи­большая скорость истечения характерна для низких концентра­ций ПАВ. Время достижения постоянной скорости истечения

С ростом концентрации ПАВ увеличивается.

Незначительный объем раствора (единицы процента от об­щего объема первоначально содержащейся в пене жидкости)

Т, мин

Рнс 30 Кинетические кривые исте­чения жидкости нз пен при различ­ном содержании сульфонола ttii-i. П.„ „. у — объем вытекшей жидкости; для б - Д V/Дт - изменение скорости истечения во времени.

65

У. мл _______ , AV/&T.мл/мин

1В г, мин

К_ Q49

AV/M,мл/мин

%,/2,МиН

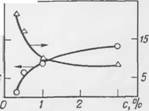
Рис. 31. Зависимость времени истечения половины объема жидкости и максималь­ной скорости истечения жидкости из пены от концентрации сульфонола НП-1 в рас­творе.

Удерживается в пленках продолжительное время с сохранением устойчивой структуры пены. Это соответствует превращению пленок пены в соединенные адсорбционные сольватирован - ные слои.

Увеличение содержания ПАВ в иепообразующем растворе существенно влияет на кинетику истечения жидкости из пены: уменьшается скорость истечения жидкости и увеличивается про­должительность истечения, выраженная через т1/а (время исте­чения половины объема жидкости) (рис. 31). Это можно свя­зать с повышением структурно-механической прочности пленок, увеличением объема мицелл и усилением взаимодействия меж­ду адсорбционными слоями.

Кинетика истечения жидкости нз пен изучалась многими ис­следователями. Были получены уравнения, описывающие этот процесс; некоторые из уравнений приведены в монографии Бн - кермана [80].

Одна из первых работ, посвященных изучению кинетики ис­течения жидкости, принадлежит К - Н. Арбузову и Б. Н. Гребен­щикову. Взяв в качестве объекта исследования растворы сапо­нина, они показали, что при наступлении стационарного потока жидкости процесс истечения описывается эмпирическим урав­нением

Где т—время истечения; а—доля выделившейся жидкости, %.

Поскольку кривые синерезиса оказались аналогичными кри­вым адсорбции, авторы предложили для связи величины K и концентрации с ПАВ использовать формулу Фрейндлиха:

C"/ft = m (4.7)

Где /I. т — константы.

Из уравнений (4.6) и 4.7) можно получить:

Т 100

Конечно, это эмпирическое уравнение имеет существенные недостатки. Оно справедливо лишь для заключительной стадии
процесса, когда скорость истечения замедляется. Не будучи основанным па какой-либо физической модели, оно формально описывает явление. Происхождение констант п и гп и п физи­ческий смысл неясны. Однако заслуга авторов состоит в том, что они фактически впервые исследовали истечение жидкости из пен как самостоятельное и своеобразное проявление их раз­рушения.

Для теоретического и экспериментального исследования ис­течения жидкости из пен многие авторы используют физические модели этого явления. Прн этом скорость потока жидкости под действием силы тяжести определяют по уравнению Пуазеиля:

U = г2Др/(8г]/г) (4.9)

Где г и 1х — радиус и длина капилляра в пене в момент т; ДР=р— рх—раз­ность давлении па концах капилляра; 1) — вязкость жидкости.

Уравнение Пуазейля справедливо для пстсчеиня жидкостей пз цилиндрического капилляра, а так как жидкость в пене течет в канале треугольного сечения, то его применение к пенам пред­полагает определенные допущения.

Рассматривая пену как группу капилляров, в которой течение жидкости подчиняется уравнению (4,9), авторы работы [144] получили следующее выражение, описывающее кинетику истече­ния жидкости пз пены:

Т= (V + algV + Ь)/к (4.10)

Где V — объем жидкости, вытекшей за время т; а, Ь и K — константы.

Это уравнение справедливо для истечении жидкости практи­чески па протяжении всего процесса, за исключением началь­ного н конечного периода. Значения постоянных к, и п b зави­сят от природы и концентрации ПАВ в растворе. Однако, как указано в работе [145], интерпретация физического смысла этих констант затруднительна, вследствие чего уравнение имеет ограниченное применение.

Используй принцип подхода Гпббса к физической модели ис­течения (течение жидкости между двумя плоскими пластинами, расположенными параллельно и неподвижно относительно друг друга), Росс рассматривал параллельные пластины не непо­движными, а допускал, что расстояние между ними изменяется пропорционально содержанию жидкости в пене в данный мо­мент. На основе этой модели было получено уравнение

Т= l/ft(K0-V)"-lyfeV0» (4.11)

Где V0 и V—объем жидкости в пене в начальный момент и ко времени т Соответственно.

К сожалению, сведении о применимости этого уравнения для обработки практических результатов исследований пет.

5*

67

Джекобн с соавт. [146] для теоретического вывода уравне­ния истечения жидкости в качестве модели пены приняли две
параллельные пластины, расстояние между которыми изменя­ется по высоте и во времени. Применив к этой модели закон Пуазейля и приняв 6 = /sV (б — толщина стенки пузырька), они получили уравнение следующего вида:

Где V — объем жидкости вытекшей за время т; а и B — константы.

Справедливость зависимости (4.12) проверяли, используя растворы нескольких пенообразующих веществ с концентрацией — 2%. Проверка показала, что значения констант а и b имеют большой разброс. Уравнения (4.11) и (4.12) имеют одинаковую запись при K = B3L(4а2) и Vo = 2A/B, однако отличаются перемен­ной V.

V-

П. М. Кругляков и П. Р. Таубе в качестве модели взяли систему цилиндрических капилляров. Приняв, что процесс исте­чения жидкости описывается соотношением (4.9), авторы теоре­тически рассмотрели истечение жидкости нз пен при следующих допущениях: Др = const и N0/Lo = N/L [145]. Последнее допуще­ние, показывающее, что отношение удельного числа капилля­ров N (число капилляров, приходящееся на единицу площади) к их длине /, пропорциональное высоте столба пены, в процессе истечения не меняется, справедливо только в том случае, если при истечении жидкости обе величины (N и I) уменьшаются. В действительности отношение N/1 может уменьшаться, увели­чиваться пли оставаться постоянным. Радиус капилляра г толь­ко уменьшается. Поэтому полученное авторами уравнение

8lrv

Будет правомерным только в том случае, если отношение N/1 В процессе распада пены увеличивается, т. с. явление «спрямле­ния» капилляров преобладает над уменьшением их удельного числа.

Исходя из этих допущений, авторы получили следующее ко­нечное выражение, описывающее процесс истечения жидкости из пен:

2V

V/2 = т/V — L/V0 Или т= ^ (2 — (4-14)

Где kl=2/V0 V0 и V—соответственно начальный объем жидкости и объем жидкости, вытекшей за время т, отнесенные к единице площади сечения стол­ба пены; D0 — начальная скорость истечения.

Проверка показала, что k при увеличении вязкости раство­ра изменяется незначительно, a v0 — существенно, особенно при различных концентрациях ПАВ.

Справедливость уравнения (4.14) проверяли [146], исследуя пены, полученные тремя способами: встряхиванием в цилинд­

Ре
Pax, просасываипем раствора через пористый фильтр под дав­лением атмосферного воздуха (прибор Арбузова — Гребенщико­ва) и перемешиванием неновзбпвателем. Для получении иен использовали растворы различных ненообразующих веществ, причем в некоторых опытах в раствор вводили загустители. Ки­нетика истечения жидкости пз пепы, полученной встряхиванием в цилиндрах, вполне удовлетворительно описывается уравне­нием (4.14). Для пен, полученных из некоторых растворов с по­мощью прибора Арбузова—Гребенщикова и пеиовзОпнателя, наблюдались значительные отклонения от этого уравнения, осо­бенно в начальный момент истечения жидкости.

Поскольку процесс истечения жидкости из пен графически выражается сложной зависимостью, аппроксимация которой простым математическим выражением затруднительна, предло­жен способ описания кинетики сииерезиса несколькими различ­ными уравнениями

Каждый из трех участков кривых истечения жидкости нз пен (см. рпс. 30) в соответствии с работой [147] можно аппрокси­мировать уравнением (4.16), V=Vo—1/(/гт) и уравнением (4.10). Эти уравнения, выведенные для описания синерезиса водных пен, достаточно хорошо отражают кинетику истечения жидкости из пен на основе органических растворителей, хотя концентра­ция ПАВ, необходимая для получения таких пен, во много раз больше.

Если принять, что V — объем жидкости, вытекающей за вре­мя т, a Vo — начальный объем жидкости в столбе пепы, то согласно работе [148] для скорости истечения будет справедли­во уравнение

DV/dx = k(V0 — V) (4.15)

Где п—постоянная, определяемая условиями пенообразования.

Интегрируя уравнение (4.15) прн 1/ = 0 для т = 0, а также приняв kln=iu, получим выражение

V0l(V0-V)=>e-xnX (4.16)

Которое аналогично приведенному в работе [144]. Из пего можно получить две важные характеристики: время вытекания половины объема жидкости х1/г и время «жизни» иены т*. В первом случае V = 0,5Vo. Поэтому из уравнения (4.16) сле­дует:

Т1/а = '^(Ш37а (4.17)

Условно приняв V(rk) =0,99 V0, найдем:

Хк =ул4,605/сс (4.18)

Параметры а и п можно найти экспериментально. Результа­ты эксперимента и расчета оказались близкими: погрешность составила менее 2%.

Скорость истечения жидкости под действием силы тяжести согласно работе [149] можно выразить уравнением вида

DV/dx = 0,5flV„ (Вт, + 1 (4.19)

Где В — эмпирическая константа.

Это уравнение хорошо описывает процесс медленного исте­чения жидкости из пены и хуже — быстрого истечения. Досто­инством этого соотношения является наличие лишь одной про­извольной константы.

Исходя из теории прочности жидкости, разработанной Я. Б. Зельдовичем, применительно к малоустойчивым пенам, разрушение которых определяется разрывом пленок пузырьков, авторы работы [150] предложили уравнение, описывающее про­цесс истечения жидкости, сосредоточенной в каналах Плато и освободившейся при разрушении пленок пузырьков:

Г = Г„ехр[ 1 + £/Тиу1 ]-М (4.20)

Где V и V0 — объем жидкости, вытекшей из иены к моменту т, и исходное ко­личество жидкости; k, П, d — константы.

Справедливость уравнения (4.20) для описания процесса синерезиса в целом авторами не проверялась, однако экспери­ментально подтверждено снижение скорости истечения жидко­сти с увеличением концентрации ПАВ.

В связи с развитием методов фракционирования с помощью пен проводились теоретические и экспериментальные исследова­ния процесса истечения жидкости из движущегося потока пены [151]. Скорость истечения жидкости из движущейся пены обыч­но представляют в виде функции основных параметров процес­са п конструктивных характеристик аппарата. По другим же работам полученные зависимости при введении определенных допущений могут описывать процесс истечения из таких пен для стационарных условий. Так, авторы работы [152] в каче­стве модели приняли течение жидкости в капилляре среднего диаметра D, допустив, что число капилляров (каналов Плато — Гиббса) пропорционально числу пузырьков. Для этой модели

Уравнение Пуазейля принимает вид

<•(4-21>

Где (1—I)—доля поперечного сечения, занятого каналами Плато, по кото­рым происходит истечение жидкоеm

Используя уравнение материального баланса жидко i фазы во времени при истечении жидкости в стационарных условиях, авторы [152] получили основное выражение для общего объема вытекшей жидкости за время т:

1де v д н m — эмпирические константы.

Справедливость уравнении (4.22), а также трех других, опи­сывающих процесс при различных вариантах движения пены, доказана экспериментально.

Предположив, что скорость разрушения пленок пропорцио­нальна их числу п н единице обьема пены:

Dn/dx = —Кп Где X — коэффициент пропорциональности.

И полагая, что весь объем жидкости V, выделяющейся при раз­рушении пленок, сосредоточен в каналах Плато:

V~nd

Где 3 — средний диаметр пузырьков, с учетом n~l/d:> пли d~ п~1/з

Автор работы [110] получил уравнение зависимости объема жидкости, остающейся и иене, от времени:

I/ = V0e~*x (4.23)

Где V. — константа.

Уравнение (4.23) справедливо для заключительной стадии сннерезиса. Экспериментальная проверка этого уравнения по­казала недостаточную сходимость с теоретической зависимо­стью, причем отклонение тем больше, чем меньше высота столба пены [140].

Следует отметить, что, несмотря на применение различных подходов п физических моделей, некоторые нз приведенных уравнений (табл. 4) эквивалентны и отличаются лишь констан­тами. Так, при V0=100% и V = (100—а) % уравнение (4.23) ста­новится аналогичным уравнению Арбузова — Гребенщикова (4.8), в котором константы связаны зависимостью

V — сп/т

Уравнения (4.14) и (1.22) также эквивалентны при ид=1>о И M = /ETVo/2.

Все уравнения, приведенные в табл. 4, имеют определенные ограничения, поскольку процесс очень сложен и до сего вре­мени не описан простым математическим выражением. В связи с тем что процесс истечения в отдельных случаяг аппроксимиру­ется экспоненциальной зависимостью, Росс [153] приводит ана­логии с физическими процессами, характеризующимися умень­шением потенциальной энергии и подчиняющимися экспоненци­альному закону. Так как в пенах имеет место истечение жидко­сти н диффузия газа, можно рассматривать разрушение пены как рассеяние запасенной ею потенциальной энергии, соответ­ствующей сжатому газу, находящемуся под давлением выше атмосферного, избыточной поверхности раздела газ — жидкость и некоторому избытку жидкости, истекающей по сети каналов

Таблица 4. Основные уравнения, описывающие процесс истечения

I'O н V — объемы жидкости

Физическая модель истечения

Математическая зависимость

Область применения уравнения

Вытекание обусловлено коалесценцией, скорость которой пропорциональ­на числу пленок

Истечение из цилиндри­ческих капилляров при постоянных ДР и N/1

Истечение нз цилиндри­ческого капилляра

Истечение из группы ка­пилляров (уравнение Пу - азейля)

Истечение между парал­лельными пластинами с изменяющимся расстоя­нием

То же. Расстояние изме­няется пропорционально объему жидкости

V= Vo(l—е~ftT) k=cn/m; С—концентра­ция ПАВ; Лит — кон­станты

V—Vo (1—е~~*т) я — Константа

V~Vo ( I-hU/2 )

Fe=2/lV, v0 — иачальна5 скорость истечения

Чд и m — константы

Y+alg V=kx—b A, b и k — константы

2 а ( 1

А и Ъ — константы

/1+VJftr

И — константа

Заключительная стадия процесса, Ј»<i>„aKc

Заключительная стадия процесса

Условия: вся жидкость сосредоточена в каналах Плато; малые значения Р и }i.

Пены для разделения ве­ществ

За исключением началь­ной и конечной стадий процесса

Сильно обводненные пе­ны (Р<10; т1/а=2— 8 мин)

Примечание. Формулы в тексте в основном соответствуют записи, приведенной шей из пеиы жидкости V от времени т. * Карбокснчетлцеллюлоза.

Плато — Гиббса. Этой гидро - и газодинамической аналогии соот­ветствуют процессы истечения жидкости *из пен и общее изме­нение объема газа в пене, т. е. не учитываются другие факторы разрушения пен.

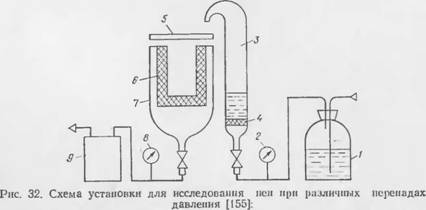
Существенное влияние на свойства пен и процессы их раз­рушения оказывает давление в каналах Плато — Гиббса. В се­рии работ П. М. Круглякова с болгарскими и отечественными физнкохнмнками [154—156] исследован и предложен способ ускорения истечения жидкости из пен под действием больших градиентов давлений (dpldh^>pg) в каналах Плато за счет создания зоны пониженного или повышенного давления в ниж­ней (пли верхней) части столба пены. Схема эксперименталь­ной установки показана на рис. 32.

При больших перепадах давления в каналах Плато с учетом

Жидкости н. ч пен

Начальный н иытскшиП к DpuMuilu X Псслсдпи. шиыо растворы Способ получения тмш И IV ]1 л 1 ура Водные 0,2—2,0%-иые раство­ры сапонина Разрежение под пористым фильтром [1431 — — П Ю] Водные растворы сульфонола с добавками КМЦ* и электро­лита и без них Встряхивание в цилиндрах; взбиваиис мешалкой; барбоги - рование; разрежение под филь­тром |145] Водные 0,05%-ные растворы додецилбеизолсульфоиата Na с 0,01—0,001% NaCl Пропускание воздуха через по­ристый фильтр |152] Водный раствор лаурилсульфа­та Na; 0,01%-иый раствор лаурилсульфата Na и лаурино - вого спирта; игепон Т Пропускание воздуха через пористый фильтр [114] Водные 2%-ные растворы три­тона Х-100, алкилсульфатов натрия и амфотерных ПАВ Пропускание воздуха через по­ристый фильтр [146] Смазочные масла различной вязкости То же [1421

В оригинальных работах. Формулы в таблицах даны в виде зависимости объема вытек-

Общепринятых допущений (вся жидкость сосредоточена в ка­налах, скорость течения на поверхности каналов равна нулю, скорость течения в канале подчиняется уравнению Пуачейля, радиус кривизны каналов одинаков по длине канала) получены уравнения, характеризующие истечение жидкости из пси [154]:

Т = с(1/^-1/г02) (4.24)

И кинетику установления капиллярного давления в каналах Плато:

Т = ок) (4.25)

Где г0, г — соответственно начальный радиус пузырька и в момеиг времени т; Рок, Рк—соответственно начальное капиллярное давление в каналах Плато и в момент т; с — коэффициент, c=nLl3[(2Spuf)', ц — динамическая вязкость;

73

1 — сосуд для очистки и увлажнения воздуха; 2— манометр; 3 — сосуд с раствором; 4— пористый фильтр; 5 — стеклянная 'крышка, 6 — стакан из пористого стекла; 7 — стеклян­ный кожух; S — вакуумметр; 9 — ресивер.

1К и U — соответственно общая и эффективная (с учетом примыкающих при­токов) длина канала; / = 3,3-Ю-3 — геометрический коэффициент; Др0 — пе­репад давлений между пространством над иеной и под фильтром.

Из уравнения (4.25) путем подстановки геометрических ха­рактеристик пентагонального додекаэдра как элемента пенной структуры авторами [154] получено выражение, не содержащее неизвестных параметров:

Т= 1100 2(Р2к Р~ок) (4-26)

Где H — высота столба пены.

Проверка зависимости (4.26) по экспериментальным данным показала, что она справедлива для пены, полученной из раство­ра додецилсульфата натрия, и не выполняется для пепы из рас­твора неионогенного ПАВ [154].

Исследования процесса синерезнса, проведенные Л. Л. Куз­нецовой н П. М. Кругляковым [156], свидетельствуют о непра­вомерности предположения, что скорость течения на поверхно­сти канала равна нулю. По разработанной авторами методике исследования течения растворов ПАВ по каналам Плато по­стоянного сечения получены экспериментальные значения ско­ростей течения в зависимости от площади сечения каналов. Сравнение их с теоретической средней линейной скоростью те­чения показало, что режим течения всех исследованных раство­ров существенно отличается от течения в капилляре с непод­вижными стенками. Так, скорость течения на поверхности кана­лов с D>120 Мкм составляет от 25 до 80% от общего значения средней линейной скорости для исследованного интервала раз­меров каналов (для анионного и неионогеипого ПАВ). Истин­ная же скорость течения в каналах в 2—5 раз больше, чем рас­считанная скорость для неподвижной поверхности каналов. Ав­торы делают вывод о подвижности стенок каналов, причем эта подвижность неодинакова для пленок различных типов и зави­сит также от площади сечения каналов. Полученные в работе [148] результаты имеют важное значение для развития теории истечения жидкости из пси.

Многие приведенные уравнения, описывающие процесс исте­чения жидкости из пен, включают определяемые эксперимен­тально константы, в отдельных случаях не имеющие конкрет­ного физического смысла. Применимость уравнении иногда ограничивается отдельными стадиями процесса, свопеiними ис­следованных пен и т. д. Это обусловлено тем, что пена как объ­ект исследования и протекающие в ней процессы разрушения, в частности истечение жидкости, весьма сложны и не всегда могут быть описаны строго математически.

Большой интерес представляют теоретические исследования истечения жидкости из пен В. В. Кротова [4, 157, 158). Его ра­ботами обоснованы требования, обеспечивающие адекватное описание процесса истечения жидкости на основе представлений механики сплошных сред. Такими требованиями являются не­обходимость учета прн рассмотрении процесса истечения пло­щади сечения пенного столба, которая значительно превышает площадь сечения единичного пузырька. Кроме того, локальные параметры пены не должны существенно изменяться па рас­стоянии порядка радиуса пузырька.

На основе данных представлений показано [157], что стро­гое описание процесса истечения жидкости пз пены возможно не из рассмотрения процесса на уровне отдельных каналов Плато н пленок, поскольку такой подход может обеспечить по­лучение лишь эмпирических или полуэмпирнческих зависимос­тей, а нз исследования их на локальном уровне. Введенное В. В. Кротовым [157] понятие гндропроводпостп II дисперсной системы (пепы) представляет собой сумму капаловой 11 к и пле­ночной #„ гидропроводностей: Н = НК + Н„. Прн выводе уравне­ния для определения Як и Яп автор рассматривал [159] двух­мерную пену (монослой пузырьков между двумя параллельны­ми поверхностями), однако полученные результаты можно от­нести и к трехмерной пене, которой свойственно отсутствие ре­гулярной структуры. Не исключено, что такой подход может внести некоторые погрешности.

Использовав уравнение для скорости вязкого ламинарного течения жидкости между двумя параллельными поверхностями:

62

Vn = - щ- РG Cos а

Где I| — динамическая вязкость жидкости; а — угол, характеризующий про­странственное расположение пузырьков пеиы.

Уравнение для средней скорости течения в каналах Плато [159]:

Г2

% = зоег, pgcosa

И данные работы [4], автор вывел следующие уравнения для составляющих гидропроводностн пены:

R-V3 У?2 Vs

Яп = 2-10-з-^р-; //к = 3,З. Ш-»-^-5- (4.27)

Где Vn и VK — соответственно доля объемной плотности пены, приходящаяся на пленки и каналы Плато; R — радиус эквивалентного пузырька; г — ра­диус кривизны поперечного сечения поверхности канала Плато; б — толщина пленок.

Из уравнений (4.27) выведено условие, характеризующее чисто «капаловый вариант» гндропроводпости пены: V„3/VK2<§;1.

Локальная объемная плотность пены, как и гидропровод- ность, представляет собой сумму V=V„+VK. Для описания истечения жидкости в постоянном гравитационном поле при «каналовом варианте» истечения (можно пренебречь величина­ми Яп п Уп) и при зависимости локальной объемной плотности V только от высоты в столбе пены h и времени т получено урав­нение

DV ,- d2V Р tdV* dV ,, ооч

= Р (4.28)

Где величины а и Р выражены в виде //=3,3-10~3R2V2Tx=UV2 S= = 9,5- Ю-4 a/? Vl/2/r] = p V"2; 5= — «коэффициент сннерезнса», см2/с [160].

Уравнение (4.28) является квазилинейным уравнением в частных производных второго порядка параболического типа. Некоторые наиболее важные частные случаи решения подобных уравнений приведены в работах [158, 1С0].