Welding as a fabrication technique presents a number of difficult problems to the design and manufacturing community. Nowhere is this more evident than in the aerospace industry with its emphasis on performance and reliability and yet where materials are seldom se­lected for their weldability.

Developments in calculating the thermal cycle and elastoplastic stress-strain cycle have been slow because of the inherent complex­ity of the geometry, boundary conditions and the nonlinearity of ma­terial properties in welding.

However, the exponential growth in computer performance com­bined with equally rapid developments in numerical methods and geometric modeling have enabled computational weld mechanics to reach the stage where it can solve an increasing number of problems that interest the industry specially in pipelines, power plants, refiner­ies and pressure vessels, nuclear reactors, building and bridges, automotive, trucks and trains, ships, offshore structures, aerospace structures, micro electronics and many others.

Although the ability to perform such analyses is important, the real justification for computational weld mechanics is that it is be­coming cheaper, faster and more accurate to perform computer simulations than to do laboratory experiments. Taken to the extreme all relevant decisions would become based on computer simulations. For example since nuclear testing in the atmosphere has been banned, this has actually occurred in nuclear weapons design, a field at least as complex as welding. It is unlikely that computational weld mechanics will eliminate all experiments in welding. Instead, com­putational weld mechanics is likely to increase the demand for accu­rate constitutive data, particularly at high temperatures, and to in­clude the effect of changes in microstructure. Also it will not eliminate the need for experiments that simulate or prototype proc­esses and products. However, it will dramatically reduce the number and cost of such experiments and greatly enhance the accuracy and significance of the data obtained for each experiment. In the automo­tive industry, CAE (Computer Aided Engineering) is said to have re­duced the number of prototypes required from a dozen to one or two.

In the next few years, digital data collection of not only welding experiments but of production welding will be coupled to computer models. The computer models will use the experimental data to ad­just the parameters in the computer model. The experiment and pro­duction system will use predictions from the computer model to con­trol the process. The mathematics of this is called a Kalmann filter. In this case, the computer model and experiment are tightly con­nected. Neither could exist without the other. At this point religious wars between experimentalists and theorists will become meaning­less.

Furthermore, models can be examined to provide insight that could never be obtained by experiment. For example, it is well known that work piece distortion caused by welding austenitic stainless steel is some three times greater than that caused by weld­ing carbon steel. By analyzing models in which each property is var­ied separately, the sensitivity of the distortion to each property can be computed. This would provide the knowledge needed to under­stand the greater distortion in austenitic steel. Of course, this is not possible experimentally.

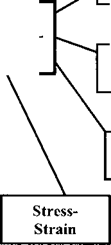
In its narrowest sense computational weld mechanics is con­cerned with the analysis of temperatures, displacements, strains and stresses in welded structures, Figure 1-1.

Figure 1.1: Computational welding mechanics draws on the disciplines shown above to compute the temperature, microstructure, stress and strain in welds. (PDE/IE-stands for Partial Differential Equations/ Integral Equations)

In its broadest context, it is an important element of Computer Aided Design (CAD) and Computer Aided Manufacturing (CAM). Computer modeling, in general provides the capability of storing vast amounts of data; of organizing and storing relations between data in databases or knowledge bases; and of using these data to compute or predict the behavior of products, processes or systems in the real world. On one hand, it can be viewed as a set of analytical tools for determining the mechanical response of a work piece to a given welding procedure. On the other hand, it can be viewed as a

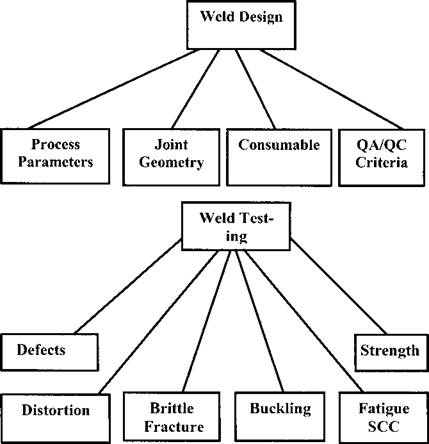
design tool for predicting the quality of a weld and the deformation, Figurel-2.

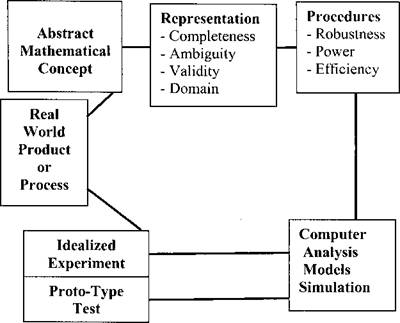
It is necessary at the outset to clearly fix the relationships of com­puter methods to experimental investigation, Figure 1-3.

Experiments tend to fall into two broad categories. Some are based on clearly understood theory where a strong attempt is made to exclude extraneous factors. Measurement of Young’s modulus or thermal conductivity of a particular alloy fall into this category. On the other hand, when experiments deal with complex phenomena that do not have a clearly understood theory, a strong attempt is made to include any factor that may be relevant. Developing a nar­row gap welding process is an example of this second category.