Геодезический изотензоид
 28 ноября, 2012
28 ноября, 2012  admin
admin Такое очертание, характерное для равнонапряженной волокнистой структуры, обычно получается при спиральной намотке. Движение волокна принимается тангенциальным к полюсным утолщениям (рис. 16.8) [15]. Положение каждой точки на этом пути определяется ее меридиональным гх и окружным г2 с радиусами. Эти радиусы связаны с координатами х я у, определяющими очертания фигуры, следующим образом:
Гх - р------------ ,
_я[1 + (у')2]1/2
Где у' я у" — первая и вторая производные у по х.
Главные силы, действующие на мембрану в результате внутреннего давления Р, определяют по формулам:
Рг
Меридиональная N4 = ; (16.3)
Окружная N9 = JЈ.[2 — г2/га]. (16.4)
В равновесном напряженном состоянии значения прочности волокна по главным направлениям равны этим силам, что позволяет записать следующее выражение:
T==7tf6w = 2-tg2a> {16"5>
Где a — угол намотки. При геодезической намотке справедливо уравнение
|
(16.1) (16.2) |
X-sin а = const. (16.6)
|
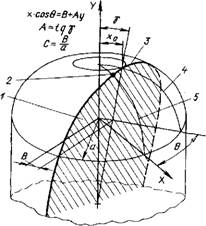
Рис. 16.9. Геометрия изделия при плоскостной намотке: 1 — плоскость намотки; 2 — точка Р {х, у)ш, 3 — движение волокна в плоскости; 4 — базовая меридиональная плоскость; 5 — меридиан, проходящий через точку Р |
В точке касания а = 90° и
Sin а = xjx, (16.7)
Где х0 — диаметр утолщения.
Решение уравнений (16.5) и (16.7) дает координаты контура. Их решение в общем случае может быть получено путем поэтапного интегрирования на ЭВМ. Возможны и графические методы решения [14, 16]. Когда tg2 а — 2, уравнение (16.5) применять нельзя. Самый простой способ решения за этой точкой перегиба заключается в продлении радиуса сферы до пересечения с полюсным утолщением.

 Опубликовано в
Опубликовано в