Gaussian Surface Flux Distribution
 6 марта, 2014
6 марта, 2014  admin
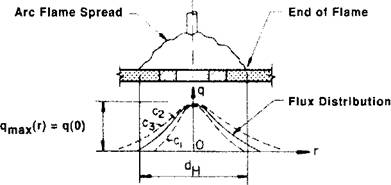
admin In the ‘circular disc’ model proposed by Pavelic et al [40], the thermal flux has a Gaussian or normal distribution in the plane, Figure 2-6:
q(r) = q(0)e~cr (24)
where:
q(r) = Surface flux at radius r(Wjm2)
<7(0) = maximum flux at the center of the heat source (W/m2)
С = distribution width coefficient (m~2) r = radial distance from the center of the heat source (in)
|
Figure 2-6: Circular disc heat source [40] |
A simple physical meaning can be associated with C. If a uniform flux of magnitude q(0) is distributed in a circular disk of
diameter d = 2/Vc, the rate of energy input would be rIV, i. e., the circle would receive all of the energy directly from the arc. Therefore the coefficient, C, is related to the source width; a more concentrated source would have a smaller diameter d and a larger value of C. To translate these concepts into practice, the process model for the normal distribution circular surface of the heat flux for laser beam welding and submerged arc welding, is illustrated in Figure 2-7.
|
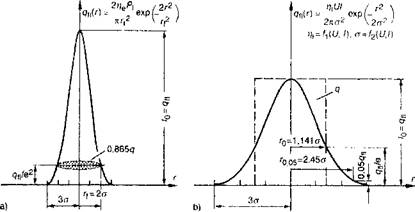
Figure 2-7: Normal distribution circular surface heat source and related parameters ( radial distance from center o) by laser beam welding (a) and by submerged arc welding (b); with laser efficiency coefficient rie, the laser power Pb the focus diameter 2rf, the arc efficiency coefficient r|t - voltage of arc V, the current I, the maximum flux at the center of the heat source q(0) equal intensity I0, Euler number e=2,71828...; from Sudnik (unpublished) and Radaj [3]. |
The curve of the submerged arc welding is wide and low and the curve of the laser beam welding is in contrast, narrow and high. The laser beam has high intensity and a small diameter. The laser power Pi on the surface of the workpiece considering the efficiency coefficient is used as heat flux (power) q and/or heat power density qfl. The circular normal distribution is described by the
focus radius rf = 2a which contains 86% of the heat power.
The arc welding has less intensity and larger diameter. The arc power VI on the surface of the workpiece considering the arc efficiency coefficient is used as heat flux q and/or heat power density qf}. For the circular normal distribution two different
descriptions are used. The source radius ro. os, in this heat power density is reduced by 5% (Rykalin [37] or the source radius r0 of a same power source with constant heat power density (Ohji et al [51, 73]). The particular problem which exists for the definition of the heat source in arc welding is that both the arc efficiency rj / and the radial distance from the center a are functions of the voltage V and the current I of the arc (Sudnik and Erofeew [72]).
The effective radius r0 and/or г0.оа of the circular surface heat source are derived from the maximum surface width of the molten zone. The heat flow density from the surface qfl(x, y) for known rf)
and/or Г(Ю5 is defined from the power data of the weld heat source, considering the heat transfer efficiency. This is shown in Figure 2-7 for the laser beam welding and arc welding. If weld metal is added the related heat should be considered.
Experiments have shown that a significant amount of heat is transferred by radiation and convection from the arc directly to the solid metal without passing through the molten pool. Based on this observation, Pavelic et al. [40] developed a correlation showing the amount and the distribution of this heat over the solid material. In their study, provisions were made for convective and radiative losses from the heated plate to the surroundings as well as variable material properties.
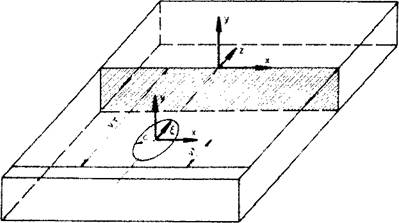
Friedman [43] and Krutz and Segerland [42] suggested an alternative form for the Pavelic ‘disc’. Expressed in a coordinate system that moves with the heat source as shown in Figure 2-8, Eq. (2-2) takes the form:
д(х,0 = Ще^1/с2е-^2/сг (2-2)
wc
where:
Q = energy input rate (W)
с = is the characteristic radius of heat flux distribution (m)
It is convenient to introduce an (x, y, z) coordinate system fixed in the workpiece. In addition, a lag factor т is needed to define the position of the source at time t = 0, Figure 2-8.
|
Figure 2-8: Coordinate system used for the FEM analysis of disc model according to Krutz and Segerlind [42] |
The transformation relating the fixed (x, y,z) and moving coordinate system (x, y,0 is:
£ = z + v(T-t) (2-3)
where v is the welding speed (m/s). In the (x, y, z) coordinate system Eq. (2-2) takes the form:
q(x, z,t) = A£Le-3*7c2e-3[z + v(r-o f/c2
For x2 + £2 <c2. For л:2 + £2 > c2 ,q(x,£,t) = 0
To avoid the cost of a full three-dimensional FEM analysis some authors assume negligible heat flow in the longitudinal direction; i. e., BT/dz = 0 • Hence, heat flow is restricted to an x-y plane, usually positioned at z = 0. This has been shown to cause little error except for low speed high heat input welds [41]. The disc moves along the surface of the workpiece in the z direction and deposits heat on the reference plane as it crosses. The heat then diffuses outward (x-y direction) until the weld cools.

 Опубликовано в
Опубликовано в