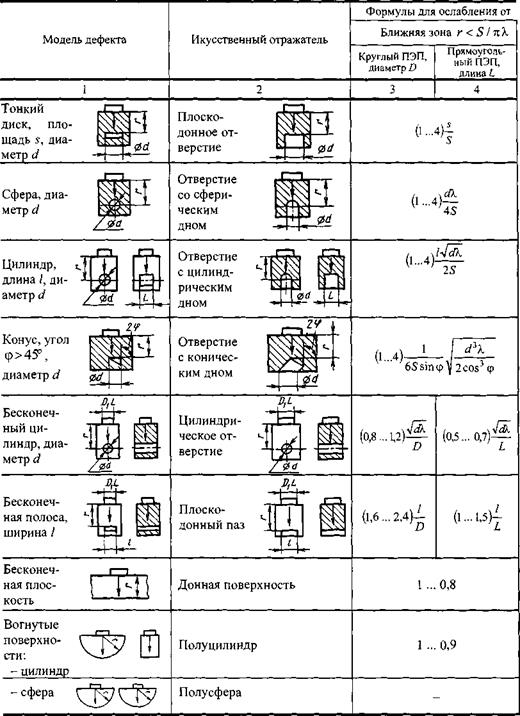
Сводка формул дана в табл. 2.1 [132, 247], где Р0 и Р' - амплитуды излученного и принятого сигналов; S - площадь пьезо­пластины; г - расстояние преобразова­тель-отражатель. Для учета затухания формулы граф 3-5 следует умножить на е-25'.

Отражатели разделены на три груп­пы: компактные, все размеры которых меньше неоднородностей поля излучения преобразователя; протяженные в одном направлении (паз, длинный цилиндр); протяженные в двух направлениях (плос­кость, вогнутые поверхности). Отражатель считают протяженным, если его размер больше ширины области эффективно взаимодействующего с ним поля преобра­зователя.

Каждой группе отражателей соответ­ствует своя зависимость (графа 8) ампли­туды эхосигнала от приведенного рас­стояния r/N, где N - длина ближней зоны преобразователя. Заштрихованные облас­ти на кривых определяют вариацию ам­плитуды под влиянием формы и длитель­ности импульса. Кривая Д относится к донному сигналу, уточненное ее значение приведено на рис. 1.15. Формул для расче­та эхосигналов от вогнутых цилиндриче­ских отражателей в ближней зоне нет. По формулам, представленным в табл. 2.1, нельзя точно рассчитать эхосигнал от во­гнутых цилиндрических поверхностей стандартных образцов СО-1 и V-1, так как из-за их небольшой ширины возникают отражения от боковых поверхностей, уве­личивающие эхосигнал на 1 ... 2 дБ от расчетного значения.

В формулах для ближней зоны (гра­фы 3, 4) интервалы численных коэффици­ентов определяют диапазон разброса ам­плитуд эхосигналов в зависимости от рас­
стояния отражатель-преобразователь, фор­мы и длительности импульсов. Они также зависят от формы пьезопластины. Расчет в переходной и более точный расчет в ближней зонах круглого преобразователя следует вести по общей формуле (гра­фа 8), используя графики и коэффициент вида дефекта А из графы 6 или 7.

Коэффициенты А определяются от­ношениями характеристических размеров отражателя b (диаметра d, ширины или длины I) к длине волны. Если Ь>Х, то такие модели, как диск, сфера, короткий цилиндр, полоса, дают такие же эхосигна - лы, как имитирующие их искусственные дефекты (отверстия с плоским, сфериче­ским или цилиндрическим дном, паз). При Ъ < X для искусственных дефектов коэф­фициенты, показанные в графе 6, сохра­няются, а для моделей изменяются. В гра­фе 7 они приведены для случая b « X для продольных волн в материалах с коэффи­циентом Пуассона 0,3. Формулы граф 3 - 5 соответствуют случаю b > X. Коэффици-

, 1вг<о3

ент А = 1,5 — для плоскодонного от­верстия диаметром d «X указан соглас­но экспериментальным данным К. Киму - ры. Теоретические оценки В. Н. Данилова

дают А = 0,6

Отметим, что применение формул имеет ряд ограничений. Ниже рассмотре­ны эти ограничения и способы устранения некоторых из них.

• Формулы соответствуют коротко­волновому приближению представления акустического поля преобразователя S » X2.

• Формулы приведены для прямого совмещенного преобразователя. Для пре­образователей с акустическими задержка­ми вводят мнимые излучатель и приемник, как показано в разд. 1.3.2. Формулы аку­стического тракта для изделий со сфери­ческой или цилиндрической поверхностью рассмотрены в [119, 324].

• Предполагается, что диаметры сфе­ры и цилиндра d значительно меньше рас­стояния преобразователь-отражатель. Для

дефекта А

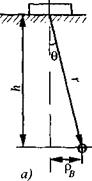
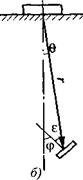
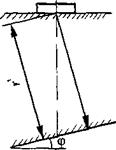
Рис. 2.30. Отражатели, смещенные от оси преобразователя, и
наклонные отражатели

расчета отражения от цилиндра с диа­метром d, соизмеримым с расстоянием до него (например, от канала ротора), нужно использовать формулу

Р0 ^ у 8r3(l + af/2r) ’

где г - расстояние до ближайшего к пре­образователю края отражателя. Она пере­ходит в формулу табл. 2.1 при d « г. По­добным образом трансформируется фор­мула таблицы для сферического отража­теля

Р Sd

Ро 4Ar2(l + dilrf

• Диаметр диска, длина или ширина короткого цилиндра, конуса, паза не должны превосходить 0,2 от размеров D и L преобразователя. Ограничение для диска снимают, применяя АРД диаграммы (см. разд. 2.2.2.2).

• При отражении поперечных волн диаметр цилиндра в графах 5 и 6 должен быть > ТК (для продольных волн - > 0,4А,). Для сферы подобные ограниче­ния существуют, но количественно не ис­следованы. В целях устранения этого ог­раничения расчет выполняют по графикам (см. разд. 2.2.2.2).

Формулы табл. 2.1 позволяют рас­считать максимальное значение эхосигна - ла от дефекта, расположенного на опреде­ленном расстоянии от преобразователя. В дальней зоне это соответствует положе­нию отражателя на оси преобразователя. В ближней зоне максимальный эхосигнал может давать отражатель, лежащий в сто­роне от оси. Приведем формулы для рас­чета значений эхосигналов от моделей дефектов, расположенных не на оси в дальней зоне преобразователя, в том числе дефектов, наклонных к оси (затухание не учтено). Для повышения точности учтено ослабление амплитуды излучаемых про­дольных волн вследствие частичной трансформации в поперечные.

Боковое цилиндрическое отверстие диаметром d (рис. 2.30, а):

(2.2)

Здесь Ф(9) - диаграмма направленно­сти преобразователя (см. табл. 1.10); 9 - угол между его осью и направлением на цилиндр; у(9) - коэффициент трансфор­мации продольных волн в поперечные при излучении, показанный на рис. 1.51.

Диск диаметром 2Ъ и площадью s (рис 2.30, б), наклоненный под углом ср к поверхности ввода:

sS <гЛ л. 2/л2Уі(2^Й8ІПє)

—x(9)eos8cose02(9) ')■ .------- L,

2kb sine

(2.3)

где s = ф - 0 - угол падения на дефект.

Полоса шириной 2 Ь, наклоненная под углом ф:

F bsjl Р0 ~ (Л)3/2

(2.4)

Плоскость под углом ф к поверхно­сти ввода (рис. 2.30, в):

^=27хХ^С°50ф2^’ (2'5)

где г’ - кратчайшее расстояние от преоб­разователя до плоскости. Формулы (2.2) -

(2.3) экспериментально не проверялись.

Пример 2.1. Сфера какого диаметра d даст такую же амплитуду сигнала, как плоскодонное отверстие диаметром d = 3 мм, если Я, = 1,5 мм?

Одинаковые амплитуды эхосигналов два компактных отражателя дадут, когда их значения А одинаковы, причем d > Я; отсюда

dj{ 4Я) = mf 2/(4Я2 );d = nd'2/Я = я32/і,5 = 19 мм.

Пример демонстрирует плохую выявляе - мость округлых дефектов по сравнению с пло­скими, перпендикулярными к оси преобразователя.

Поясним физический смысл приве­денных формул [247]. Площадь преобра­зователя входит в числитель всех формул для дальней зоны, потому что лучи от преобразователя расходятся в виде диа­граммы направленности и угол расхожде­ния лучей тем меньше, чем больше пло­щадь преобразователя. Дискообразный отражатель подобен излучающему преоб­разователю. От него лучи также расходят­ся в виде диаграммы направленности, по­этому площадь диска входит в числитель первой формулы.

Сравнение формул для дальней зоны показывает, что ослабление донного сиг­нала с расстоянием происходит медленнее (пропорционально Иг), чем эхосигнала от диска или сферы (пропорционально 1 /г2),

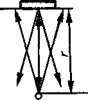
Рис. 2.31. К закономерностям ослабления
эхосигнала с расстоянием:

а - для сферы; б - для плоскости

ослабление эхосигнала от цилиндра - в промежутке между ними (по закону 1 /гш). Такие закономерности объясняются следующим. Лучи от излучателя расхо­дятся, поэтому амплитуда убывает, как 1 /г. Диск или сфера - как бы вторичные излучатели. Попавший на них сигнал пе - реизлучается в обратном направлении (рис. 2.31, а), поэтому амплитуда опять убывает, как Иг. В итоге ослабление про­порционально 1/г2.

Донная поверхность играет роль зер­кала (рис. 2.31, б). Отраженные от него лучи можно рассматривать как излучен­ные мнимым излучателем, зеркально­симметричным действительному (показан штриховыми линиями). Расстояние от не­го до приемника 2г. Именно по закону Н2г убывает донный сигнал. Цилиндр в плос­кости, перпендикулярной к оси, - малень­кий отражатель, лучи от которого расхо­дятся как от сферы. В плоскости вдоль оси - отражение происходит как от зерка­ла. Отсюда закономерность Mrvi.

Формулы для ближней зоны исходят из предположения о нерасходимости энер­гии акустического поля.