Современное сварочное производство имеет возможность ис­пользовать для сварки и резки все виды энергии.

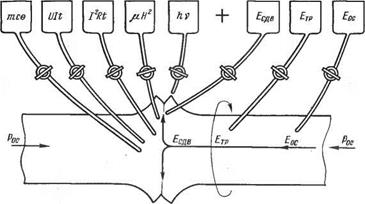
Рассмотрим для стыковых соединений это энергетическое мно­гообразие в подробностях, иллюстрируя поступление энергии в зону сварного соединения посредством модели, показанной на 444

Рис. З Л 7. Возможные источники энергии активации стыкового свариваемого контакта

рис. 3.17. Здесь источники энергии представлены в виде резервуа­ров, из которых технологом в зону сварки может быть введена любая энергия, по какой угодно программе. Количество и скорость ввода энергии регулируются некоторыми вентилями. Для схемы, приведенной на рис. 3.17, приняты такие обозначения:

/лее — энергия экзотермических химических реакций: газо­вой горелки, термитной реакции, печного нагрева;

PRt — энергия Джоуля в любых ее низко - и высокочастотных проявлениях;

UIt — энергия плазмы, различного рода разрядов: искровых, дуговых, тлеющих, взрывоискровых (оплавление), электронного луча;

— энергия магнитных полей при любых частотах; hv —• энергия фотонных потоков при квантово-лучевых про­цессах (лазеры).

Отдельно и особо следует рассмотреть механическую энергию. На схеме она представлена в трех видах: £сдв — энергия сдвига; Етр — энергия трения; Еос — энергия осадки. Как понимать эти виды энергии? Как известно, первый закон термодинамики

р = re*l(2t) = усТ (3.38)

говорит о том, что любая механическая энергия — растяжения, сжатия, сдвига — превращается в теплоту. И это превращение физически определяется сдвигами относительно друга друга: 1) элементарных кристаллов; 2) зерен (кристаллитов); 3) макро­скопических объемов металла. Выражение (3.38) не может быть отнесено к элементарным кристаллам, поскольку константы у и а свойственны массам металла.

Как было ранее показано, формулу (3.38) можно применить к элементарным кристаллам, если написать

р = т]єа/(2£) = 3&6 п, (3.39)

где уже фигурирует постоянная Больцмана k. Таким образом, тем­пературный эффект любого вида сдвига может быть вычислен. Главное в том, чтобы разобраться, какой сдвиг и в какой именно зоне контакта происходит при операции осадки или другой дефор­мирующей силе.

Рассмотрим стыковой контакт (см. рис. 3.12), на который дейст­вует осадочная сила Рос. Она вносит энергию Еос = P0Ch0c, распределенную по всему деформируемому объему. Объем этот может быть существенно разным, в зависимости от величины и скорости введения энергии — механической, электрофизической или комбинированной. Например, искровой разряд батарей кон­денсаторов создает в контакте два тончайших слоя кипящего ме­талла, осадочный удар будет концентрировать механическую энер­гию только на этот кипящий слой. Холодные слои металла, грани­чащие с кипящим, ударной осадки практически не почувствуют. Совершенно другие картины имеют место при современных режи­мах сварки контактной стыковой и трением. Здесь осадочная энер­гия рассредоточивается по всему объему нагретого металла. Од­нако самое характерное для всех процессов сварки — это то, чем завершается каждая осадочная операция, будь она медленной или быстрой, постоянной или переменной по величине.

Каждая операция осадки при стыковой сварке завершается эф­фектом межкристаллитного сдвига в целом металле, вокруг пло­скости контакта и сдвигом тонкого слоя кристаллов непосредст­венно по плоскости контакта.

Сдвиг в целом металла подчиняется, как видно, макромасштаб­ным измерениям и потому может с какой-то степенью достовер­ности оцениваться величиной температуры, которая определя­ется формулами (1.31) и (1.41), как показано здесь,

Тсдв = Ttd'wJW) + I/Ги, ’ (3,40)

где tC№ — время, в течение которого осуществляется межзеренный сдвиг. Для стыковой контактной, для стыковой трением это время надо определять по-разному. При контактной стыковой сварке методом сопротивления детали в течение всего времени нагрева находятся под давлением, при этом время осадки и время нагрева равны. При контактной стыковой сварке методом непрерывного оплавления время осадки есть время только осадочной операции, завершающей нагрев. При сварке трением два времени: нагрева и осадки. Обычно давление нагрева и собственно давление осадки различны.

Таким образом, температурный вклад в нагреваемый объем металла по формуле (3.40) следует вычислять дважды и с учетом 146

указанных различий по давлениям. Но при современных относи­тельно малых скоростях действия собственно осевой силы Рое температурный эффект от этого будет получаться ничтожно малым. Следует вспомнить и еще одну формулу:

Рослое

4 IаКус V t0

в которой рос —• осевая осадочная энергия; hoc — осевой размер осадки; toc — время этой осадки.

Какая же из этих двух формул [(3.40) или (3.41) ] более досто­верна? И могут ли они вообще определять одно й то же число? Одинаковые числа они давать не должны не только потому, что может быть некоторая неполная согласованность физических кон­стант: і] и Кус. Дело в том, что формула (3.41) с ее энергией /?ос/іос дает температурную вспышку от действия осевой силы, а формула (3.40) с ее константой г] — от перпендикулярно направленных радиальных сил сдвига. Однако эффект сдвига возникает от дей­ствия осевой осадочной силы Рос, которая и является первоисточ­ником всей сдвиговой деформации. Металл, однако, нагревается при всякой пластической деформации. В формуле (3.38) содержится и тепловая константа с, и деформационная г). Из формулы (3.40) поэтому получим более достоверные значения температуры, воз­никающей при деформации, чем из (3.41).

Сравним формулы (3.40) и (3.41) посредством численных рас­четов. Для этой цели используем опытные данные ВНИИЭСО для конкретных условий холодной сварки. Надо сказать, что из всех способов сварки давлением процесс холодной сварки до сих пор оказывается теоретически наиболее загадочным. Тем не менее физическая картина сваривания будет как-то связана с расчетным числом. Сваривались медная и алюминиевая прово­лока диаметром 3,5 мм. Длина выступающих из зажимных гу­бок концов устанавливалась, в зависимости от диаметра, в оп­ределенных соотношениях l/d. Осадочная энергия р00 измерялась в момент завершения осадки, измерялось время осадки toc (с). На основании этого была составлена таблица опытных и расчетных данных (табл. 3.1).

Если эти температурные расчеты дали в какой-то мере даже завышенные значения температур, то возникает недоумение: как же может происходить не только схватывание, но и сваривание проволок при таких в общем-то низких температурах? Видимо, здесь надо исходить из следующих физических представлений.

1. Каждый акт сваривания как явление формирования непре­рывной кристаллической структуры по плоскости контактирова­ния происходит со скоростью звука. Для расстояний, сравнимых с размерами атомов и кристаллов это время составляет 10-13 с.

2. Каждый процесс сварки давлением завершается эффектом атомно-кристаллического сдвига по плоскости контакта. На этот сдвиг тратится или вся, или частично осадочная энергия. Атомно-

араыетр	Медь	Алюмннвв
Опытные числа и физические константы
Ud,%	0,6 80	1,0 50
Рос» Дж/см3 Yкус, Дж/см2»с,/2"еС Ч, Дж'с/см3	1300 3,77 1200	550 2,35 1028
Расчетные числа
Гспв. °С — см. формулу (3.40)	129	203
Тср, °С — см. формулу (3.41)	48	76

кристаллический сдвиг по плоскости контактирования создаст в тонком слое кристаллитов или даже элементарных кристаллов температурный импульс, всегда превышающий точку плавления для слоя металла, участвующего в эффекте сваривающего сдвига.

Исходя из этих положений, произведем некоторые дополни­тельные расчеты. Осевая осадочная энергия Р0choc по плоскости контакта превращается в радиально расходящуюся энергию сдвига

Ес „в = peHBz6S, (3.42)

если считать г --- число слоев элементарных кристаллов, участву­ющих во взаимном сдвиге; 6 — параметр решетки кристалла; S — площадь контактирования.

Ранее, в гл. 1, была получена формула (1.39) для расчета тем­пературы в плоскости контакта Тю если в плоскости контакта концентрируется любая энергия. Для энергии сдвига [см. фор­мулу (3.42) 1, как видно, можно написать расчетную формулу типа (1.39), если сохранить в ней константы, действительные для микро­объема. Это значит, что равенство (1.39) надо изменить так:

. qt —3k0nS2x (3.43)

при тех же самых х — 2

Поскольку qt — pCJ№zbS, подставляя

pemz6S — 12knQS -/at,

получаем выражение для температуры

0 в ргЫ(Шп -/at).

В данном случае речь идет о сдвигах на расстояние параметра решетки, поэтому

і — 1 hmi

где v3B — звуковая частота, определяемая как скорость звука евв, отнесенная к параметру кристалла 6.

Сев = VWv* (3.45)

где G — модуль сдвига, Н/ма = кг-м/^-м3).

На основе этих выводов можно представить себе сущность хо­лодной сварки в виде физической схемы, излагаемой следующим образом. Как было показано расчетами, осадка в макрообъеме создает недостаточный нагрев. Оценим количественно температуру, достигаемую при плоскостном сдвиге [см. формулу (3.44)]. Из нее получаем равенство

Для холодной сварки меди и алюминия снова используем опыт­ные рекомендации ВНИИЭСО:

Ш. % Рсдв- Дж/ем*

Для меди...................................................................... 75—125 1250—1450

» алюминия........................................................... . 50—100 550—800

По этим данным формула (3.46) определяет следующее число слоев элементарных кристаллов, участвующих во взаимном сдвиге:

Число слоев г............................................................ 140—120 115—80

Общая толщина слоев Д, мкм................................ . 0,35—0,3 0,33—0,23

Как видно, толщина сдвига настолько мала, что не просматри­вается с помощью обычных систем оптических микроскопов. И тем не менее плоскостный эффект сдвига, завершающий осадку, дает тот самый необходимый для сваривания высокотемператур­ный импульс, который и завершает процесс формирования не­прерывной кристаллической структуры по контактной плоскости. К моменту сваривающего микросдвига контактная плоскость об­разуется внутренними слоями металла. Поскольку все загрязнения были вытеснены осадкой, сдвиг происходит по идеально чистому металлу. Все изложенные здесь расчеты и соображения относятся к холодной сварке. Для других процессов сварки давлением, на­пример сварки трением, экспериментальные и расчетные числа будут совсем другие.

Те же формулы (3.44) и (3.46), имея в своем составе скорость звука, для трения должны давать значительно меньшие значения. Это следует из формулы (3.45), в которой модуль сдвига G сильно падает для горячего металла, особенно нагретого до температуры, близкой к точке плавления. Согласно выражениям (1.39) и (1.51), температуру в плоскости контакта за счет энергии трения можно определить так:

У = Ртр^срЯ Vtyp iq qj

тр 240 V ‘ '

где ртр — энергия в контакте, вызываемая трением; <Зср — сред­ний размер диаметра свариваемой детали; п — частота вращения детали, об/мин; /тр — длительность операции трения.

Завершающая осадочная операция в зоне свариваемого кон­такта обеспечивает подъем температуры в результате межзерен - ного радиального сдвига, который может быть учтен формулой

Тояв = 2yctoc/№) + 1/Т~ • (3'48)

При практических расчетах по этой формуле toc — время дей­ствия завершающего осадочного давления.

Относительная деформация е при сварке трением для разных металлов и различных осадочных давлений получается в преде­лах 0,5—0,7, редко достигая 0,8. Этот размер можно приближенно определить по формуле (3,31)

е лг 1 — d2/Da, (3.49)

где d — диаметр свариваемого стержня; D — диаметр деформи­рованного контакта.

Учитывая все это, произведем конкретные расчеты для сварки трением круглых стержней диаметром 2 см. Средний размер диа­метра будем, следовательно, принимать dcp = 1 см. Опытные дан­ные ВНИИЭСО для стержней из стали СтЗ: ртр = 50 Дж/см4; tip — 6,25 с; п = 1000 об/мин. Коэффициент аккумуляции

уґКус — 1,47 Дж/см2-с*/2«°С.

Температура плоскости контакта за счет операции трения по формуле (3.47)

^ 50-3,14-1000-2,5 л„аоп

1 ---------- 240-1,47 “ 111

По размерам D и d, согласно формуле (3.49), относительная деформация оказалась порядка 0,7. По этим данным можно опре­делить: достаточной ли была осадочная энергия 100 Дж/см®. До­пустим, что динамическая вязкость, вычисленная для чистого железа, такая же и у стали СтЗ. Тогда

П — По (1 — Дгр/Упл) - 1836 (1 — 1112/1450) — 422 Дж«с/смэ.

Длительность операции осадки не измерялась, но это время можно считать, как и время сдвига t00, равным 1 с. Тогда

Рос = т)ва/(21) =

= 422 (0,7)2/(2-1) = 103,4 Дж/см3.

Как видно, действовавшее осадочное давление и расчетное сов­падают. Теперь можно определить, какой температурный вклад в микрообъеме создает сдвиг, завершающий сварку,

Тслв = 2,5.1/(1836-0,5) + ,1/1450 = 86 С‘

Вклад сравнительно небольшой. Он, суммируясь с температу­рой р, дает общую температуру в плоскости контакта 1112 + + 86 = 1198 °С. Действовавшее при сварке давление р превышает то необходимое, какое требует формула (1.21):

р = о, [1 + dJ(6h)h

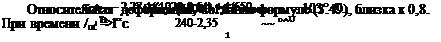
Можно проделать аналогичные расчеты и для дюралюминия. Для стержней диаметром 2 см опытные данные таковы: /тр = 3,5 с; ртр = 50 Дж/см3; /Кус = 2,35 Дж/см2-с1/2-°С ; рос — 100 Дж/см3; п — 1000 об/мин. Тогда

Суммарная температура контакта 623° меньше точки плав­ления. Осадочная энергия р = 100 Дж/см3 не только значительно превышает предел текучести при действующей температуре, но и давление, устанавливаемое из формулы (1.21). Проделанные расчеты дают основание для следующих выводов.

Основной подъем температуры при сварке трением обеспечи­вается именно операцией трения. Однако и осадочная операция, согласно формуле для температуры сдвига Тсдв, может вносить заметный вклад, если операцию осадки делать ускоренной, напри­мер вместо 1 с осаживать за 0,5 с. Однако это повлечет за собой необходимость заметного увеличения осадочного давления. Та­кого увеличения можно избежать и избегают при инерционной сварке трением. В этом процессе осевая осадка суммируется с пЪ- воротом по плоскости контакта.

Расчеты по формуле (3.44) для горячего металла дают ничто­жно малые значения температур. Для контактной стыковой сварки действительны те же выводы о влиянии осадочных скоростей на температурную картину в зоне свариваемого контакта. Здесь от­носительная деформация может достигать значения е = 80 %.

Если время осадочной операции вместо одной секунды сокра­тить до половины, то, согласно формуле (3.48), получим

Т----------------------------- 1______________ 909° Г

оде — 2,5.0,5/(1836 0,64) + 1/1450

Такая мгновенная температурная добавка в момент осадки вполне объясняет задержку охлаждения сваренного контакта, что было показано на рис. 3.14. Ускорение осадки можно получить только увеличением осадочного давления.

Осевое сжатие может быть заменено поворотной деформацией, которая в некоторых случаях может оказаться рациональной, обес­печивая после процесса оплавления устранение непроваров и не - сплошностей. Если, для примера, те же стальные стержни диамет­ром 2 см нуждались при сварке трением в осадке на 3 мм, то до­статочно одного неполного поворота, заменяющего такую осадку. Кстати сказать, инерционная сварка трением, какую по сути дела предложил А. И. Чудиков, дает большую стабильность прочности, чем принцип машин трения ВНИИЭСО, где процесс сварки за­вершается остановкой вращения и осевой осадкой. У А. И. Чу - дикова осевая осадка завершалась последним поворотом.

Неоднократно возникал вопрос о возможностях холодной сварки стальных деталей. При таком же времени осадки в 1 с, как это характерно для холодной сварки алюминия и меди, сталь сваривать весьма затруднительно. Следует учесть, что динамиче­ская вязкость, равная 1836, рассчитана для чистого железа. Для сталей это число должно быть, вероятно, большим, в такой же про­порции, как больше оказывается предел текучести стали по сравне­нию с этой же величиной для армко-железа. Практически динами­ческая вязкость перейдет за 2500. Встает вопрос, какими же дол­жны быть все зажимные и осадочные механизмы, чтобы выдержи­вать секундные удары давлением, выше 2500. Вряд ли возможны такие конструкции машин. Вполне понятно, что технология сварки пошла по пути полного освобождения от металлических зажимных и осадочных устройств. Такой технологией стала сварка взрывом. Для этого процесса формулы (3.41) и (3.48) непригодны. Первая из них потому, что физическая константа "кус, известная по стати­ческим «печным» измерениям, вряд ли справедлива для ударных процессов, а вторая, (3.48), вообще не предусматривает какого - либо значения для коэффициента динамической вязкости при тем­пературах выше точки плавления. Температура при сварке взры­вом, судя по авторитетным вычислениям, значительно превышает точку плавления. Произведем и здесь некоторые ориентировочные расчеты. Еще раз обратим внимание на две возможные ошибки, какие довольно часто допускают исследователи в различных рас­четах.

1. Все физические, электрические и механические константы для металла получены в экспериментах с печным нагревом и мед­ленным изменением действующих механических сил. Использо - 152

вать эти известные и привычные константы для многих сварочных процессов следует с большой осмотрительностью.

2. Исследователи редко относятся с полным вниманием к прин­ципу всеобщей связи явлений.

Обе эти ошибки приводят к тому, что в быстропротекающих или даже ударных сварочных процессах ведутся расчеты с пре­делами текучести, которые данным давно добыты статическими растяжениями. Мало того, почти все процессы сварки идут с ис­пользованием электрических токов, как угодно циркулирующих по свариваемым деталям и непредвиденно создающих концен­трированную в отдельных микрозонах электромагнитную и тепло­вую активацию. К сожалению, почти никогда не учитывается наличие электрических процессов в металле и в тех сварочных операциях, которые непосредственно идут под действием только механической энергии. Рассматривая, например, чисто механи­ческое понятие релаксации, определяем его как процесс перехода металла из одного структурно установившегося состояния в дру­гое, тоже стабилизированное. Длительность этого процесса, или, как говорят, время релаксации, определяется так:

т = t]/G, (3.50)

где т| — динамическая вязкость; G — модуль сдвига.

Стоит еще раз обратить внимание на выражение (3.38). Если его относить так же, как это характерно для определения (3.50), к относительному удлинению е = 1, то

t = т,/(2рсдв) (3.51)

полностью подобно определению (3.50).

Разница между этими соотношениями только та, что т — это константа для холодного металла, at — это всегда переменная величина, зависящая от действующей сдвиговой силы. Однако, если учесть, что изменения динамической вязкости и модуля сдвига от температуры почти подобны, то соотношение (3.50) для горячего и тем более расплавленного металла утрачивает, веро­ятно, смысл. Соотношение (3.50) — это понятие для макрообъемов, так как модуль сдвига — это статическая характеристика металла:

	Ов Дж/сыв	*). Дж. с/см®	т, е
Для алюминия. .	27	1028	0,038
» меди , .	44	1200	0,027
» железа.	84	1836	0,021

Время релаксации определяет поведение металла по отноше­нию к действующей на него деформирующей силе. Если время действия силы значительно больше времени релаксации [т. е. согласно соотношениям (3.50) и (3.51) t > ті, то металл ведет себя как вязкая жидкость. Это наблюдается при холодной сварке пластичных металлов: алюминия и меди. Если же время действия силы t меньше времени релаксации т, то металл ведет себя как твердое и даже иногда как хрупкое вещество. Такая картина,

15S

видимо, может быть характерна для сварки взрывом, если вести речь о макрообъемах.

Но возвращаясь снова к холодной сварке и ее конечному эф­фекту плоскостного межкристаллического сдвига, нужно при­знать, что этот сдвиг ввиду его кратковременности происходит как бы в слое твердого металла, мгновенно переходящего в состо­яние расплава и тут же снова превращающегося в твердое состо­яние. И все-таки факторы времени в этих процессах какие-то особенные. Стабилизация электронных плотностей длится в течение не долей секунд, а минут. И здесь снова приходится сталкиваться с несовместимостью явлений в металле в микро - и макрообъемах. Понятие модуля сдвига к электронным конфигурациям неприло­жимо, так же как неприложима к ним и динамическая вязкость.

Температура — это мера энергии массы движущихся частиц. Однако и частицы, т. е. атомы и свободные электроны, весьма различны не только по массам, но и по самой их природе и по их физическим свойствам. Не выходя за рамки макроскопических объемов, мы вправе оперировать с величинами модуля сдвига. Динамическая вязкость действительна для металла от кристаллов до любых макроскопических размеров. Эта физико-механическая характеристика более универсальна, чем модуль сдвига. Можно еще раз обратить внимание на подобие этих характеристик ме­талла. Формулы (3.50) и (3.51) говорят о том, что граница хруп­кого разрушения и вязкого течения металла определяется сдвиго­вой энергией, создаваемой сдвигом рсдв,

Рсдв = о/ 2. (3.52)

Если известные опытные значения модуля сдвига для холод­ного металла считать достоверными, например, для процесса сварки взрывом, то получаются значения ударной энергии сдвига, при которых пластическое (вязкожидкостное) течение металла переходит в хрупкое разрушение. Согласно (3.52), эти значения таковы: для алюминия 13 500, для меди 22 000, для железа 42 000 Дж/см3. Большие энергии уже могут вызывать хрупкое поведение твердого металла, так как время действия ударного сдвига меньше времени релаксации.

Все эти соображения, согласно приведенным выше соотноше­ниям, действительны только для холодного металла. Если, однако, обратить внимание на то, что в зависимости от температуры ме­талла обе характеристики г и G меняются подобно, то соотноше­ние t/x, равное, согласно (3.50) и (3.51),

t/x = С/(2рсдв), (3.53)

должно быть действительным и для горячего металла.

Рассмотренные здесь связи модуля сдвига и действующих энергий сдвига могут быть распространены и для растягивающих напряжений. С этой точки зрения появление трещин при осадоч­ных операциях горячего металла может быть объяснено двумя причинами.

1. Это неполностью синхронизированное изменение по темпе­ратуре модуля сдвига G и'динамической вязкости jj. Может ока­заться, что скорость изменения dGjdT будет больше дц]дТ и тогда относительно малое значение знаменателя в соотношении (3.50) даст большое значение времени релаксации. Металл поведет себя как хрупкий.

2. Такой же локализованно хрупкий эффект может оказаться мгновенно существующим, если и при относительно большом значении модуля сдвига энергия сдвига окажется концентриро­ванно очень высокой. Это будет происходить всякий раз в зонах резко концентрированных структурных включений, резких гео­метрических переходов и концентраций дефектов. Тогда, согласно (3.53), малое время действия мгновенной энергии сдвига сделает металл хрупким в зоне действия этой энергии. Отсюда и могут возникать осадочные трещины.

В связи с опасностями такого рода при стыковой контактной сварке всегда рационально обеспечивать осадку, не выключая сварочного тока. Вокруг всякого дефекта, концентрирующего механические напряжения, электрический ток и его магнитный поток создают также свои собственные концентрации. Если кон­центрация механического сдвига усиливает разрушение, то элек­тромагнитное иоле своей концентрацией может противостоять этим действиям. И концентрация тока, и магнитный поток вызы­вают значительный и мгновенный нагрев в зоне концентрации. Нагревы могут доводить металл до мгновенного плавления, когда не только залечиваются микротрещины, но и резко меняется структурная картина со всеми ее бывшими микродефектами. Влияние электромагнитных полей на трещинообразование при сварке полезно иметь в виду и исследователям прочностных свойств соединений при дуговой сварке. Оказывается совершенно небезразлично, как подводился сварочный ток к сварным образ­цам, с какой именно стороны и в каком направлении. И сварочный ток, и магнитное поле при сварке могут быть и не быть полез­ными концентраторами.

Концентрации механических напряжений могут наблюдаться и не только в технологии сварки давлением. Эффекты сдвига имеют место и за счет термических циклов, без участия сварочных осадочных давлений. Как видно, принцип всеобщей связи явлений не следует, забывать никакому технологу-сварщику.