The physical mechanism by which semiconductor LEDs emit light is spontaneous recombination of electron-hole pairs and simultaneous emission of photons. The spontaneous emission process is fundamentally different from the stimulated emission process occurring in semiconductor lasers and superluminescent LEDs. Spontaneous recombination has certain characteristics that determine the optical properties of LEDs. The properties of spontaneous emission in LEDs will be discussed in this section.

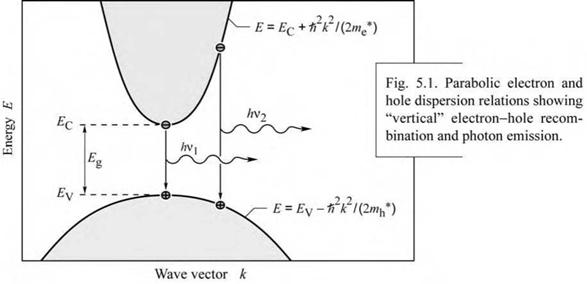
An electron-hole recombination process is illustrated schematically in Fig. 5.1. Electrons in the conduction band and holes in the valence band are assumed to have the parabolic dispersion

relations

(for electrons)

(5.5)

E = ec +

E = EV - (for holes) (5.6)

2m*

where me* and mh* are the electron and hole effective masses, h is Planck’s constant divided by 2п, к is the carrier wave number, and EV and EC are the valence and conduction band edges, respectively.

The requirement of energy and momentum conservation leads to further insight into the radiative recombination mechanism. It follows from the Boltzmann distribution that electrons and holes have an average kinetic energy of kT. Energy conservation requires that the photon energy is given by the difference between the electron energy, Ee, and the hole energy, Eh, i. e.

hv = Ee - Eh « Eg. (5.7)

The photon energy is approximately equal to the bandgap energy, Eg, if the thermal energy is small compared with the bandgap energy kT << Eg. Thus the desired emission wavelength of an LED can be attained by choosing a semiconductor material with an appropriate bandgap energy. For example, GaAs has a bandgap energy of 1.42 eV at room temperature and thus GaAs LEDs emit at the infrared wavelength of 870 nm.

It is helpful to compare the average carrier momentum with the photon momentum. A carrier with kinetic energy kT and effective mass m* has the momentum

J

2

^2 m * kT

p = m * v = J 2 m *1 m * v

(5.8)

The momentum of a photon with energy Eg can be derived from the de Broglie relation

Eg

h v

p = h к =

(5.9)

c

c

Calculation of the carrier momentum (using Eq. 5.8) and the photon momentum (using Eq. 5.9) yields that the carrier momentum is orders of magnitude larger than the photon momentum. Therefore the electron momentum cannot change significantly during the transition from the conduction to the valence band. The transitions are therefore “vertical” as shown in Fig. 5.1, i. e. electrons only recombine with holes that have the same momentum or к value. Using the requirement that electron and hole momenta are the same, the photon energy can be written as the joint dispersion relation

h 2 к 2 2 mP

h 2 к 2 2 mh

h 2 к 2 2 mr

h v = Ec +

(5.10)

- Ev +

= Eg +

where mr* is the reduced mass given by

1

11 - T- + г

(5.11)

mr

me

mh

Using the joint dispersion relation, the joint density of states can be calculated and one obtains

y/2

1

2mr V h 2 У

VE-E

P( E) =

(5.12)

g •

2П

The distribution of carriers in the allowed bands is given by the Boltzmann distribution, i. e.

= e - E/(кТ)

fB(E) = e

(5.13)

The emission intensity as a function of energy is proportional to the product of Eqs. (5.12) and (5.13),

- E /(кТ)

I (E) да JE - Eg e

(5.14)

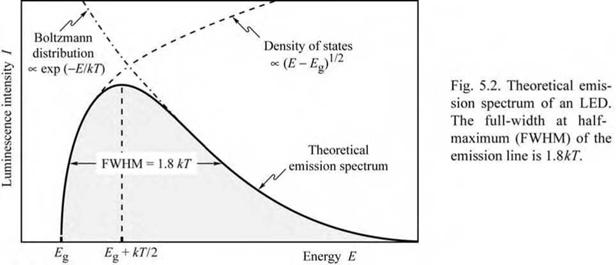
The lineshape of an LED, as given by Eq. (5.14), is shown in Fig. 5.2. The maximum emission intensity occurs at

(5.15)

E = Eg + -2- kT

The full-width at half-maximum of the emission is

		18 kT X2
AE = 1.8 kT	or	AX = ---------------
		hc

For example, the theoretical room-temperature linewidth of a GaAs LED emitting at 870 nm is AE = 46 meV or AX = 28 nm.

The spectral linewidth of LED emission is important in several respects. Firstly, the linewidth of an LED emitting in the visible range is relatively narrow compared with the range of the entire visible spectrum. The LED emission is even narrower than the spectral width of a single color as perceived by the human eye. For example, red colors range in wavelength from 625 to 730 nm, which is much wider than the typical emission spectrum of an LED. Therefore, LED emission is perceived by the human eye as monochromatic.

Secondly, optical fibers are dispersive, which leads to a range of propagation velocities for a light pulse consisting of a range of wavelengths. The material dispersion in optical fibers limits the “bit rate x distance product ” achievable with LEDs.

The spontaneous lifetime of carriers in LEDs in direct-gap semiconductors is of the order of 1-100 ns depending on the active region doping concentration (or carrier concentrations) and the