Расчет воздушио-пенных стволов струйного типа сводится к определе­нию диаметра отверстий насадки-распылителя, диаметра и длины трубы брандспойта и площади отверстий для подсоса воздуха в соответствии с уравнениями [280]:

Qp о Onto! (P-i)Qh ,Q

Где Ю|, юг, Ь)3 — соответственно площади сечения насадки — распылителя, трубы брандспойта и отверстий для подсоса воздуха; Qp и Qn — производи­тельность по раствору и пене; £ — коэффициент расхода жидкости для насад­ки-распылителя; р — давление перед стволом; ив — скорость потока воздуха; G — ускорение свободного падения.

Для расчета соь а>2 и со3 необходимы следующие данные: давление, раз­виваемое насосом, минимальная производительность ствола и кратность пены.

В качестве примера ниже приведены результаты гидродинамических испытаний лабораторного образца воздушно-пенного ствола небольшой про­изводительности. Основные конструктивные параметры ствола рассчитаны по уравнениям (9.1) при заданных значениях [5=10 н Qp=20-10_* м3/мни. Угол

Таблица 9. Результаты гидродинамических испытаний воздушно-пенного ствола Диаметр на - садкн-рас- пылителя, мм Давление перед ство­лом, р-10-', Па Расход рас­Твора, Qp-lO*. м*/мин Производитель­ность по пене (л/мин) при диа­метре трубы Кратность пены при диаметре трубы 20 мм 14 мм 20 мм 14 мм 3 2 24 140 168 5,8 7,0 2.5 25 175 210 7,0 8,5 3 26 234 280 9,0 11,0 2,5 2 14 70 80 5,0 6,0 2,5 16 96 110 6,0 7,0 3 18 140 180 8,0 10,0 2 2 10,8 52 74 5,0 7,0 2,5 11,5 80 102 7,0 9,0 3 12 96 140 8.0 12,0

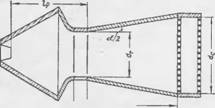
Рис. 66. Схема установки для гидро - Fidfa

Испытаний поздушно- пепных стволов: 1 емкость; 2 насос: 3 — манометр; 4 Iit'Llol Ciii'Pa Гор

-СТо

Динамических испытаний воздушно - ■ > ,-Cxj-——I------------------------ t>o------ г

Пенообра7]

ЯпДаГпЛпь

Ф

I---

Наклона насадок-распылителей к оси ствола определен экспериментально (п=5°). При использовании стволов с пена в условиях опыта ие обра­

Зуется, поскольку из-за короткой длины струи в конусной части ствола со­здается слишком низкое разрежение для подсоса воздуха. Испытания про­ведены с использованием установки (рис. 66), позволяющей измерять расход пенообразующего раствора (1% сульфонола НП-1 в воде), производитель­ность ствола по пене и кратность пены при различных давлениях раствора. Полученные результаты приведены в табл. 9.

Анализ результатов позволяет сделать ряд выводов относительно кон­структивных особенностей и режима работы пенных стволов.

Давление пенообразующего раствора перед стволом должно быть не ме­нее (2,5—3)-105 Па, так как иначе значительно уменьшается производитель­ность воздушно-пенного ствола и кратность получаемой иены. Два этих пара­метра зависят также от диаметра пасадки-распылителя, причем данные по­казывают, что диаметр 2,5 мм точно обеспечивает заданную кратность пены (Р=10).

Определенное влияние на кратность пены оказывают размеры трубы: при меньшем диаметре получается пена более высокой кратности.

В расчет сетчатого генератора пены входит определение параметров рас­пылителя и некоторых конструктивных элементов генератора. Основной пара­метр центробежной форсунки, наиболее часто применяемой в качестве рас­пылителя, является геометрическая характеристика А [282]:

Did

(9.2)

Где Dud — соответственно диаметр камеры завихрения и выходного отвер­стия; S" и S' — площади входного и выходного сечений.

С помощью геометрической характеристики А, значение которой задается в зависимости от типа форсунки [283], определяют коэффициент расхода идеальной жидкости Величина £0 необходима для расчета эквивалентной скорости реальной жидкости U8=bjfo - Скорость истечения жидкости vo можио определить по формуле

"о — ф I 2р/Р (9-3)

Где ф — коэффициент скорости, равный для воды 0,97; р — давление жидко­сти; р — плотность жидкости.

При известной массовой производительности генератора G можно опре­делить диаметр выходного сечения центробежной форсунки:

4G

-------------------------------------------- (9.4)

Диаметр камеры завихрения D определяют исходя из принятого значе­ния А и расчетного значения D. Для уточнения полученных значений прово­дят расчеты по приведенным уравнениям во втором и, если это необходимо, в последующих приближениях.

Из геометрических размеров других элементов генератора рассчитывают: Dc — диаметр пакета сеток; /д — длину диффузора; Dr и /г — диаметр и длину
горловины; /р — расстояние от распылителя до передней кромки диффузо­ра [265]. На рис. 67 показаны размеры элементов сетчатого пеногенерато­ра, подлежащие расчету.

(9.6)

Если известен диаметр пакета сеток, то прн а=8° (угол конусности) гео­метрические размеры (в мм) пеногенератора рассчитывают по эмпирическим соотношениям:

Dr = 0,72dc, ir = 0,072dc, /p = 0,65dc, 1Я = dc (9.5)

Площадь пакета сеток Fc рассчитывают в два этапа. При заданной объем­ной производительности пеногенератора Q„ (по пене) площадь пакета сеток вычисляют по уравнению

Fс = Qn/V„

Где Un — оптимальная скорость выхода пены. Величина ч„ определяется по уравнению

(9.7)

Ип = 0,25ЛУ(л6)

/?0=0,06—0,09 м2/с для обычно применяемых концентраций пенообразовате­ля ПО-1. Размер ячеек сетки 8 принимают равным 0,6—2 мм.

На этом заканчивается первый этап расчета основных геометрических размеров конструктивных элементов пеногенератора сетчатого типа.

Второй этап расчета предусматривает построение двух графических зави­симостей: расхода воздуха от давления (пли давления от кратности) и потерь давления от кратности нены. Точка пересечения полученных кривых характе­ризует расчетное давление перед пакетом сеток и расчетную кратность. Если расчетное значение кратности отличается от заданного более чем на 20%> изменяют произвольно принятый размер ячеек сетки и повторяют расчет [265].

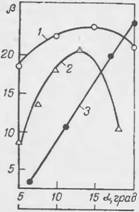
На рис. 68 и 69 представлены результаты испытаний диффузоров (четы­рех вариантов) с разными углами конусности.

Как видно из рис. 68, кратность пены с увеличением давления линейно возрастает Это обусловлено тем, что с увеличением скорости жидкости повы­шается и эжектирующая способность, а следовательно, и кратность пены. Прн увеличении концентрации ПАВ в растворе кратность пены также воз­растает.

Данные о влиянии «живого сечения» сетки на кратность пены показы­вают, что существует определенное значение F, которому соответствует мак­симальная кратность пены. По-видимому, это обусловлено тем, что при не­больших значениях F сопротивление сетки слишком велико и соответственно количество эжектируемого воздуха незначительно. При высоких значениях этого параметра часть воздуха может проходить через сетку, не участвуя в ценообразовании. Влияние диаметра горловины на кратность пены обуслов­лено снижением местного сопротивления и более эффективным использова­нием раствора в ценообразовании.

—Kr(-« U Рис. 67 К расчету сетчатого пеногенератора.

£

При испытаниях лабораторного образца пеногенератора сетчатого т Ina с автономным вентилятором (см. рис. 64) на лабораторной установке, анало-

/ 3 P W.Na о,-Ч 0,5 О, в F

I----------------- 1___________ I L------- 1-------- 1--------

' 3 СПЛВ,% 5 10 15 d'MM

Рис. 68. Зависимость кратности генерируемой пены от давления раствора (1) и концентрации ПАВ (2).

Рис. 69. Зависимость кратности генерируемой пены от угла конусности (1), «живого» сечения сетки (2) н диаметра горловины эжектора (3).

Гичной изображенной па рис 66, получены следующие результаты (1%-ный водный раствор вещества «Пена-76») ,

Давление, р О-5, Па 3 4 5 6

Производительность по пене Q-103, 90 140 180 275 м3/мии

Кратность пены 29 41,5 61 81,5

Приведенные данные показывают, что линейная зависимость кратности пены от давления сохраняется п для этого образца непогенера гора.

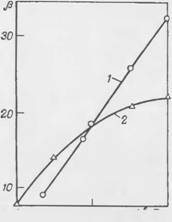
Следует заметить, что влияние давления на кратность пены неоднозначно и в значительной степени определяется как конст­руктивными особенностями генератора, так и концентрацией (а также свойствами) пенообразователя. Это хорошо подтверж­дается данными рис. 70, полученными при испытании пеногене­ратора ГВП-100 с использованием растворов хлорного сульфо­нола [284].

При расчете центробежно-осевого пеногенератора[2] принима­ются допущения: режим барботирования воздуха не зависит от режима работы пеногенератора; гидравлическое сопротивление пепоотвода не зависит от структуры образующейся пены; высо­та слоя пенообразующего раствора постоянна в течение всего времени работы пеногенератора. Основным конструктивным па­раметром является диаметр отверстий диспергатора воздуха, обеспечивающий устойчивую работу пеногенератора.

Рис. 70. Зависимость кратности пены от давления перед генератором ГВП-100 при различных концентрациях пенообразова­теля (хлорный сульфонол).

Отрыв пузырька ® поле цент­робежных сил. происходит на ран­ней стадии его формирования, поэтому равновесие пузырька не­обходимо рассматривать исходя нз строгого учета влияния на 3 4 5 р-ЩНа огрыв его объема и формы, как

Это сделано в работе [285].

В центробежном поле выталкивающая сила изменяется пропорционально отношению центробежной силы к силе тяжести. Отношение эгнх сил можно определить путем сравнения ускорений, действующих иа пузырек в центро­бежном и гравитационном полях. Это отношение (пли фактор разделения [28G]) определяется по уравнению

ЗBpRc, 900G

*р = ' опп„ (9-8)

Где п — частота вращения, мин-1; /?с— радиус барботажного барабана пено- генератора.

Используя выражение (9.8) и уравнение для силы выталкивания, полу­ченное авторами работы [285], можно найти значение выталкивающей си - . лы, действующей в поле центробежных сил:

Fn = Ржп'Яб" Ю-* [2,3л2 (г + Д») -

Г------------------------ 1 2п R2a

-2,3tfa Yf2 — R2 — 3,45/?V] +------------ -— (9.9)

Где г и R — соответственно радиус пузырька и капиллярного отверстия.

Уравнение (9.9) и соотношение F=2nRcr (см. разд. 7.2) можно использо­вать для расчета среднего радиуса пузырька.

Далее проверяют условие предотвращения обратного продавливания раствора путем определения наименьшей критической скорости воздуха в барботажном отверстии икр по уравнению, приведенному в работе [287], но с учетом влияния поля центробежных сил [выражение (9.8)].

Значение чкр для выбранного радиуса капиллярного отверстия сравни­вают со скоростью воздуха, определенной для пузырькового режима барбо­тирования V0 [286]. Если VKP^V„, то путем последовательного уменьшения размера капилляра добиваются условия икр<1>о. Для нового значения радиуса барботажного отверстия проверяют выполнение заданных требований к дис­персности пены. Если они не выполняются, расчет повторяют, изменив число оборотов барботажного барабана. При выполнении требований к дисперсно­сти пены рассчитывают параметры сжатого воздуха, геометрические размеры барабана, суммарную площадь сечения капилляров.