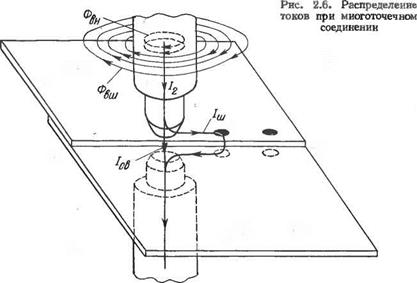
Для технолога первостепенный интерес представляет не только распределение сварочного тока в зоне свариваемого контакта, но, во многих случаях практики, и вдали от него. Для примера на рис. 2.5 и 2.6 показаны картины распределения токов при сты­ковой сварке колец и при многоточечной сварке листов.

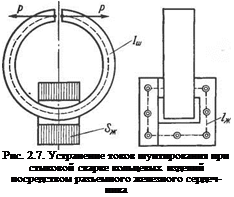
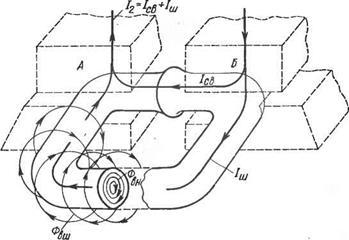
Для борьбы с токами шунтирования при стыковой сварке ис­пользуют два способа. Первый — для кольцевых деталей малого диаметра, но больших свариваемых сечений. Для них проектируют одновременную стыковую сварку двух стыков из двух полуколец. Второй способ пригоден для кольцевых изделий большого диаметра (бочки, колеса, бандажи). В этих случаях токи шунтирования можно свести до ничтожно малого значения, посредством разъем­ных дросселей (рис. 2.7). Если разъемный железный сердечник надет на кольца, то он становится одновитковым дросселем, через

Рис. 2.5. Разделение вторичного тока /х на сваривающий /св и ток шунтирования Ап при стыковой сварке кольцевых изделий

который идет ток /ш. Коэффициент самоиндукции такого дросселя определяется так:

L = 4зт2рЗнЛж. (2.26)

где п — число витков (п — 1); Sm — площадь сечения активного железа сердечника; /ж — длина средней магнитной линии по сердечнику (рис. 2.7).

Если положить, что максимальная индукция, допустимая в сер­дечнике, В = 1,8-104Тл, то, поскольку

В = р#; Я = Пи,

получаем

р = 1,8-104н//ш, (2.27)

где « = 2(^ + 6) — периметр проводящего контура ветви шунтирования.

При этом индуктивное со­противление одновиткового дросселя

v j 2я:/4я1,8- 104и5ж

ДР - - /ш/ж10» •

Для нормальной ты 50 Гц

v 725ж103 1П_„

Лдр— . ш ,

где Sm — в м*; Хдр-в Ом. Если напряжение на свариваемом контакте £/*, то

£/, = 1ШХЛР = 1ш72т8т'/{1шЩ,

откуда

« 14U2.

В этом отношении U% — среднее значение напряжения на свари­ваемом контакте в процессе его нагрева. Для стыковой сварки оплавлением это £/оп — среднее значение напряжения в период установившегося взрывоискрового процесса.

Шунтирование тока при точечной сварке — явление значи­тельно более сложное. Бороться с ним физически невозможно. Поэтому представляется необходимым определять масштабы шун­тирования, для того чтобы иметь представление о том, насколько может уменьшиться сваривающий ток, рассчитанный на единич­ную точку.

Полное сопротивление ветви шунтирования (рис. 2.8) с уче­том индуктивности определяется так:

Zm = ]Л(Дш+Гш)2 + *ш. (2-28)

По Л. Р. Нейману, активное сопротивление любого провод­ника из любого металла следует рассчитывать с учетом критерия х 1см. формулу (2.22) 1

Дш = Яош(1+ о. бх/х) = Доша, (2.29)

где #ош — сопротивление постоянному току при равномерном его распределении по сечению проводника.

Индуктивное сопротивление проводника, создаваемое внутрен­ним магнитным потоком, рассчитывают по формуле

Хш = Дош0,84х = Romb. (2.30)

Для точечной сварки, если только точки не ставят непосред­ственно одну рядом с другой, составляющая гт относительно мала по сравнению с Rm. Тогда, учитывая формулы (2.29) и (2.30), находим

zm = Дош /У+Ь*. (2.31)

При сварке листов значительной ширины постоянный ток мо­жет растекаться между двумя точками на ширину эквивалентной полосы Лэ (рис. 2.9). Ее размер можно определить приближенно из следующих условий.

Согласно известной электротехнической формуле,

(2-32)

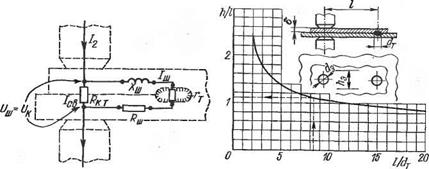
Рис. 2.8. Схема распределения сопро - Рис.- 2.9. График изменения эквива - тивлений и токов при точечной сварке леитной ширины ветви шунтирования с шунтированием в соседнюю точку тока при точечной сварке

При значениях Ud > 3, что почти всегда имеет место при точечной сварке, можно из выражения (2.32) получить (2.33) (2.34)

Этот размер и определяется по графику рис. 2.9.

Если расчет токов шунтирования ведется для немагнитных металлов, у которых р = 1, то индуктивностью ветви шунтиро­вания можно пренебречь и вести расчет только активного сопро­тивления по формуле (2.29). К сожалению, как показано ниже, величину критерия х приходится определять весьма кропотливо. Во избежание этого вместо активного сопротивления переменному току по формуле (2.32) или (2.33) рассчитывают сопротивление постоянному току и мирятся с тем, что расчетное значение тока шунтирования получается несколько выше действительного. Наи­меньшее расхождение получается, естественно, при точечной сварке униполярным или выпрямленным током.

Для сварки переменным током, да еще и магнитной конструк­ционной стали, расчет токов шунтирования может быть выполнен по следующей методике.

Согласно (2.18) и (2.20), имея в виду возможный максимум В = 1,8-104 Тл, подставляя значение р из формулы (2.27) в (2.22) и принимая / = 50 Гц, получаем

/ш = 0,04S2/(«px2). (2.35)

С другой сторона, учитывая выражение (2.31), J __ Ущ __ Ущ

Приравнивая формулы (2.36) и (2.37), определяем

В этом равенстве Um наиболее достоверно определять так:

Urn « W,. (2.38)

поскольку графики, приведенные на рис. 1.25, показывают возмож­ность такого приближения.

При расчете Лэ для полос эта величина может получаться больше ширины полосы. В таких случаях, очевидно, следует брат в расчет реальный размер деталей. При большой толщине листов и размер 6 может оказаться больше двойной эквивалентной глубины проникания тока. Эти дополнительные электромагнитные факторы, так же как и эффект близости, вносят в расчет неточность. Не­смотря на эти обстоятельства, расчет токов шунтирования надо производить хотя бы с той целью, чтобы расчетные значения насто­раживали технолога и давали ему сигнал о необходимости экспе­риментальной проверки влияния шунтирования на размер ядра.

Для того чтобы не забывать, что токи шунтирования оказы­вают практически незаметное влияние на силу суммарного вто­ричного тока, следует привести численный пример.

Полное сопротивление вторичного контура при сварке пер­вой, единичной, точки таково:

1/('к + М2+Хк

При сварке второй точки с шунтированием

У 2

У (гк + Яэкв)а Ч" Хк

В этих равенствах гт принимается как среднее значение сопро­тивления, от которого идет ветвь шунтирования; RaKB — экви­валентное сопротивление двух параллельных сопротивлений,

1/^?экв = 1/Гг ~Ь 1/^ш-

Допустим случай даже очень сильного шунтирования, когда Rm » гт. Тогда эквивалентное сопротивление двух параллельных цепей

/?днв — гв/2.

Рис. 2.10. Измеренные значения вто­ричного тока /2 и тока шунтирования 1т при сварке стальных листов толщи­ной 4 мм (диаметр электрода da = = 13 мм)

„ — плоское поле; Ф_,„ — поле коль- Mu МК цевое

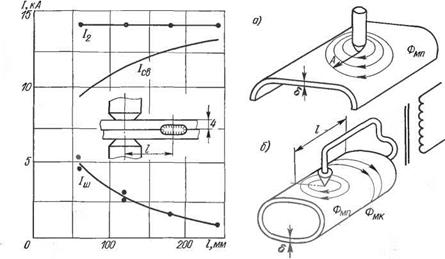
Рис. 2.11. Магнитные потоки в свари-
ваемых деталях:

Если иметь в виду, что индуктивные сопротивления контуров обычно раза в 3 больше активных гк, то видно, что вторичные токи /2ед и /2Ш практически мало будут различаться.

Наличие токов шунтирования скажется не на суммарном вто­ричном токе, а на токе сварочном, поскольку

1% — ha + Im, (2-39)

а согласно равенствам /свгт = ImRm; /ш = /св^т/^ш.

/ов = Ш + rJRm). (2.40)

Отсюда видно, что малое сопротивление ветви шунтирования мо­жет значительно снизить сварочный ток по сравнению с тем зна­чением, которое рассчитано или установлено для единичной точки, т. е. когда Rm = со. Снижение сварочного тока при Rm = = (5н-6)' гт практически окажется незаметным для приборов, из­меряющих вторичный ток /2. В качестве примера такого рода на рис. 2.10 приведены измеренные значения токов вторичного и шунтирующего при сварке стальных листов толщиной 4 мм. Как видно, шунтирование при малых расстояниях между точками весьма заметно снижает сварочный ток.

В крупногабаритных изделиях из конструкционных магнит­ных сталей могут концентрироваться заметные магнитные по-

77

токи. В сварочных контурах точечных и шовных машин изделия представляют собой фактически некоторые дроссели с переменной индуктивностью. Индуктивность оказывается переменной вели­чиной по причине искажения симметрии плоского поля Фп, если точки ставятся от края к середине (рис. 2.11, а). Индуктивность, создаваемая за - счет кольцевого поля, переменна в зависимости от размера I — длины свариваемой детали, вдвинутой в контур машины. Оценивать величины индуктивных сопротивлений можно на основе следующих соотношений.

Среднее значение напряженности плоского магнитного поля (рис. 2.11, а)

Яср = 1Ц2пА12),

где А — радиус наиболее удаленной магнитной линии. Отсюда среднее значение абсолютной магнитной проницаемости, согласно (2.35),

рср = 18 ОООяА//.

Коэффициент самоиндукции тороида, который создается одним свариваемым листом толщиной б,

LMn = 2рб In (2AldT).

Соответственно индуктивное сопротивление, свариваемого листа за счет плоского поля Фп

Хмв = 2я/2р81п(2Л/сгт) 1(Г9' = 2я/2 180°0лЛб-ln(2A/dT) 10*.

Для частоты / = 50 Гц

Хмв = - 36000е^1п (?ЛАУ 10-6) (2.41)

где dT — диаметр точки; б — толщина свариваемого листа.

Все геометрические размеры даны в м; / — в А; Хмп — в Ом.

Для листов толщиной более 4 мм размер двойной эквивалент­ной глубины проникания магнитного потока следует проверять по формуле

Лэкв = ^/Ш> (2-42)

Если оказывается, что 2ДЭКВ < б, то в формуле (2.41) следует принимать в расчет именно величину 2ДЭКВ, поскольку только такой слой в толстых листах концентрирует в себе магнитный поток Фмп.

При сварке цилиндрических изделий, когда на токоведущие штанги (рис. 2.11, б) надевается замкнутая магнитная масса, в ней кроме плоского поля Фмп концентрируется еще и кольце­вое Фмк. Этот поток создает дополнительную индуктивность, ко­торую можно определить следующим образом.

Коэффициент самоиндукции тороида

/.„к = 2|л/ In (ft! rx).

Поскольку In х да 2 (х — l)/(x + 1), то можно произвести упро­щение

In г» 2(г* — гі) _ 2(Гі + 6 — rt) 26

ri г*+г1 г1 + в+г1 2гі-}-6'

Обычно при точечной и шовной сварке б весьма мало по сравне­нию с 2гг, поэтому окончательно заменяем

In (г2/гг) да б 1щ LMK = 2р/ (б/rj.

Отсюда при р = 18 000.2пгхИ

, 2-18000-2п/6

Индуктивное сопротивление (Ом) за счет кольцевого ПОЛЯ Хмк = 72 000/610-*//. (2.43)

Несмотря на то что формулы (2.41) и (2.43) дают приближен­ные результаты, расчет индуктивности производить необходимо, для того чтобы более достоверно определять электрические пара­метры сварочных машин.

Формулы (2.41) и (2.43) действительны для нормального пере­менного тока. Для машин постоянного тока или низкочастотных униполярных индуктивностями деталей следует пренебрегать. Что же касается конденсаторных машин, то при длительностях разряда, измеряемых миллисекундами, частоты получаются по­рядка сотен герц. Соответственно этому и индуктивные сопротив­ления деталей оказываются весьма чувствительными, несмотря на снижение значения магнитной проницаемости.

Главный практический вывод, который следует сделать из приведенных расчетов, сводится к следующему.

Очень часто цеховые технологи, ничего не рассчитывая, под­бирают оптимальные режимы сварки на образцах малых разме­ров, забывая о том, что будущая крупногабаритная конструкция благодаря своей индуктивности внесет очень сильные изменения в электрические параметры сварочного контура и, следовательно, в сварочный режим, отработанный на образцах, не обладавших заметной индуктивностью.

Современные программированные режимы сварочных токов могут весьма отличаться от токов синусоидальных. Однако са­мым характерным и обязательным для каждой формы кривой сва­рочного тока являются переходные режимы: нарастание тока до максимума и его спад до нуля. Какой бы ни была кривая нараста­ния и спада по своей форме (а они могут быть различны), любую ее ветвь можно представить некоторой степенной функцией.

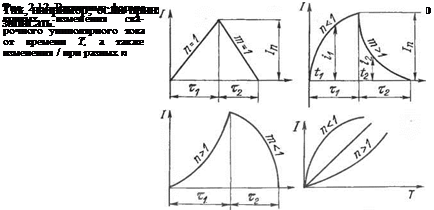В этих формулах пит могут быть любые целые или дробные числа в зависимости от того, с какой степенью точности оказывается достаточным изобразить реальную кривую тока. В нижней части рис. 2.12 наглядно представлено, как степенные показатели п и т отображают кривизну нарастания и спада по формулам (2.44) и (2.45).

В современной практике контактной точечной сварки на кон­денсаторных машинах больших мощностей скорости нарастания вторичного тока иногда достигают десятков миллионов ампер в секунду. Такие скорости изменения электромагнитной энергии вызывают эффекты механических сотрясений токоведущих де­талей. Ударные электромагнитные волны активизируют также поверхности свариваемых деталей через электронные конфигу­рации поверхностных кристаллических организаций. Как именно сказываются эти процессы на свариваемых контактах, еще никому не известно, т. е. исследований такого рода никто не произво­дил. Мало того, никто еще не исследовал и электродинамический эффект взаимодействия токоведущих штанг вторичного контура в процессе нарастания тока. Существующие расчеты сил, дей­ствующих между двумя проводниками с током, относятся к ста­ционарному значению коэффициентов самоиндукции и отобра­жают картины для неизменяющихся токов во времени.

Так, в частности, известна формула

F = 2. КГ7/2 (lib), (2.46)

в которой I — сила тока, протекающего встречно в проводах круглого сечения, расположенных параллельно друг другу на расстоянии между осями Ь на длине I.

Как известно, каждый контур тока в зависимости от его гео­метрии и формы проводников обладает своим коэффициентом самоиндукции, в связи с чем и электродинамические силы F для разных контуров различны.

Формула (2.5) и вытекающая из нее формула (2.7) уже пока­зали, что во всех зонах действия электромагнитной силы она ока­зывает механическое давление. Однако еще более существенную роль ударное магнитное давление оказывает на металлическую поверхность, активизируя ее и вызывая экзоэлектронную эмис­сию. Кроме того, магнитное давление создает и эффект тепловыде­ления на металлической поверхности, который может заметно сказаться при сварке цветных сплавов на мощных конденсатор­ных машинах.