Computational Results
 9 июня, 2014
9 июня, 2014  admin
admin Computational results are presented for the experiments described by Barlow [5]. It is a weld deposited on a low carbon steel plate of thickness 19 mm. The weld length is about 250 mm. In order to minimize end effects, the length and width of the plate are chosen to be 1224 mm and 500 mm, respectively. This is consistent with
Barlow's experiment where the plate is considered infinite in length and width.
The temperature-dependent thermal conductivity and volumetric heat capacity are taken from Reference [15].
The total number of elements is 12092 and the total number of nodes is 15323. Most elements are concentrated along the weld path for high resolution in the HAZ, where the temperature gradient changes rapidly during welding.
Several levels of grading elements are used [16] to allow a coarse mesh in the far weld area. This reduces greatly the computing cost without losing significant accuracy.
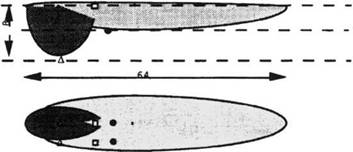
The size of the weld pool, see Figure 3-7, was determined from the experimental results in Reference [5]. The same weld parameters as condition 1, Reference [5], were applied in order to compare the computed results with the results of experiment. The nominal power input is 3.2 kJ/mm and the weld speed is 6.67 mm/s.
|
— — — Timing line ДО# Observing point
Д □ • Figure 3-7: Frame of weld pool, the compound ellipsoid model. The temperatures at nodes inside the pool are prescribed, from [2]. |
As mentioned before, the prescribed temperature model used as the heat source is correct only in the steady state, i. e., when the heat input to the weld pool does not change with time. The results presented here are those at about 24 s from the beginning.
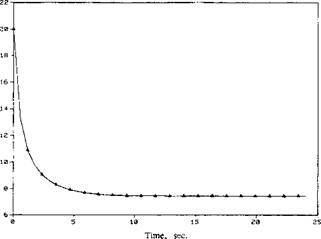
According to the node reaction to power input, Figure 3-8, it can be seen that a relatively steady state is formed as early as 5 s after striking the arc. Since the electrode is usually held still for a few seconds after the arc is struck, the total energy input per unit length (kJ/mm) is greater than the nominal value in the steady state. This total energy input is matched by adjusting the length of time the prescribed temperature weld pool is held stationary.
|
Figure 3-8: Decay of power input vs. time for prescribed temperature weld pool model for the Barlow weld. Power input is the summation of node reactions, from [2]. |
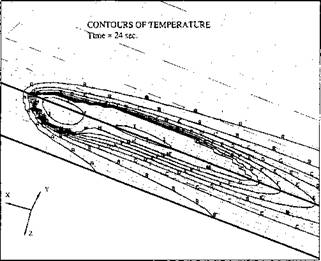
Figure 3-9 shows the contours of the temperature field. The region near the weld pool is magnified in Figure 3-10. The deep leading pool directly under the welding arc can be seen. It is suspected to be an empty hole in the real weld because the liquid metal is blown out into the shallower rear pool. The rear pool is formed to accumulate this ejected liquid metal. It is shallow and wider, so that the temperature gradient is relatively small within the rear pool. Between the front and the rear pools, there is only a thin layer of molten metal.
The temperature contours outside the HAZ are approximately elliptical in shape. A similar result could be obtained using a single weld pool, Figure 3-15.
|
D = 730; E = 908; F = 1090 Figure 3-9: The temperature field 24 s after striking the arc. The minimum temperature = 20.0°C; the maximum temperature = 1800°C, from [2]. |
|
|
|
Figure 3-10: A closer look at the weld pool and surrounding area. The min. temperature-20.0°C; the max. temperature=1800°C, from [2]. |
|
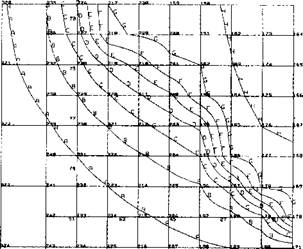
Contour Values (°С); A = 197; В = 375; С = 553; D = 730; E = 908; F = 1090; G = 1260; H = 1440; I = 1620 |
|
Contour Values (°С): A = 553; В = 709; С = 865; D = 1020; ' E = 1180; F = 1330; G= 1490; H = 1640 |
|
|
|
Figure 3-11: Temperature contours for the corresponding single weld pool model. The min. temperature= 20.0°C; the max. temperature = 2000°C, from [2]. |
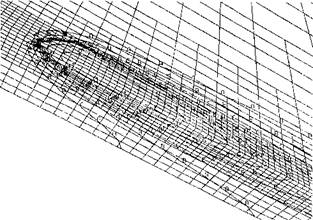
Figure 3-12: The envelope temperature contours on a section on which the temperature field projects. The numbers shown on the mesh are FEM node numbers, from [2].
Glickstein and Friedman [7] used a two-dimensional model to simulate the temperature field in a section along the weld path. Their model gave similar contours outside of the HAZ although it did not predict transient temperatures accurately inside the HAZ.
|
Figure 3-13: The thermal cycles of the nodes directly under the weld path. The node numbers are shown in Figure 3-11, from [2]. |
Figure 3-12 is the envelope of maximum temperatures in a section, through which the weld pool has passed completely. Note an envelope temperature contour is the locus of maximum temperatures projected on the plane perpendicular to the weld line. It is not the temperature contours on a cross-section at some instant of time. Note the melting point temperature is between contour G and contour F. The contour representing melting temperature envelope is superimposed on the weld pool. There is good agreement with data from experiment.
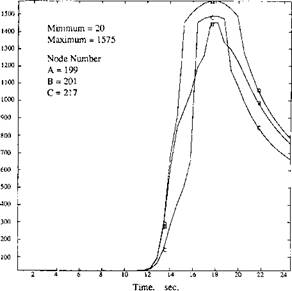
For nodes 170 and 171, i. e., for the region directly under the weld pool, the thermal cycles are simple. The HAZ is thin and basically the same as those obtained from the double ellipsoid heat source simulation. Similarly the thermal cycles of nodes 199, 201, and 217 at the widest part of the weld pool are not unusual.
Corresponding to the node numbers in Figure 3-12, a set of thermal cycle (time vs. temperature) curves are given in Figures 313 to 3-15. The computed thermal cycle within one FEM element (nodes 183, 184, 192, and 193) is obtained by interpolating the curves at comer nodes. It is found that the shape of the thermal cycle is very sensitive to the position selected.
|
Figure 3-14: The thermal cycles of the nodes along the widest side of the double weld pool. The node numbers are shown in Figure 3-12. These thermal cycles are similar to those obtained from single weld pool, from [2]. |
|
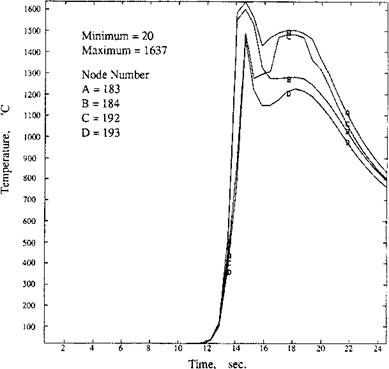
Figure 3-15: The thermal cycles of selected nodes within the bay region. Note the temperature arrest due to the second weld pool in the model, from [2]. |
The effect of the second weld pool is most apparent in the ‘bay area’. The thermal cycles at nodes 183, 184, 192, and 193 suggest a second temperature peak. Therefore this area is held at high temperature (> 1100°C) longer than other areas in the HAZ. Because of these quite different thermal cycles, temperature history dependent phenomena are expected to be quite different from other areas of the HAZ.
|
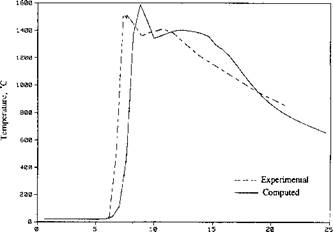
Time, sec. Figure 3-16: Comparison of the thermal cycles between computed and experimental [5] results in bay area. Note that the triggering times are set differently for ease of presentation, from [2]. |
Figure 3-16 compares experimental [5] and computed results in the bay area. Note that the agreement is excellent, which supports the analysis.



 Опубликовано в
Опубликовано в