Частотной характеристикой называется график реакции динами­ческой системы на периодическое входное возмущение.

Определение частотной характеристики объекта рассмотрим на примере системы регулирования уровня (рис. 13, а). Источником воз­мущения служит регулирующий орган / (клапан). С ним связан ге­нератор периодических колебаний. Электродвигатель 7 через редук­тор 6 вращает кривошип 2. Ползун 5, скользящий вдоль прорези тра­версы 3, шарнирно соединен с кривошипом 2 так, что тяга 4 совершает периодические колебания. Тяга 4 шарнирно связана со штоком ре­гулирующего органа /, который изменяет приток воды х (/) в резер­вуар также по периодическому закону.

Для снятия частошых характеристик применяют синусоидаль­ные и прямоугольные (рис. 13, г) периодические колебания. Периоди­ческим движением (колебанием) называется движение системы, со­стояния которой повторяются через интервал времени 7 называемый периодом.

Докажем, что при периодическом входном возмущении реакция динамической системы будет периодической с периодом Твых, равным периоду входных колебаний Тлх. Для этого предварительно разложим периодические прямоугольные колебания на серии ступенчатых воз­мущений (рис. 13, е). На рисунке для большей наглядности линии (/), которые должны сливаться, изображены, как параллельные.

Введем следующие условные обозначения: ось времени разделим на 15 отрезков с концами в точках t2, t3, .. , tl5. Слагаемые входно­го сигнала х (/) обозначим буквами русского алфавита а, б, ... , и.

На рис. 13, б приведены временные характеристики, которые соответствуют всем ступенчатым слагаемым периодического колеба­ния и обозначены аналогично возмущающим воздействиям (а, б, ... , и). Символ he(t7) будет соответствовать координатам точки пересече­ния временной характеристики (с условным обозначением Ь) и перпен­дикуляра, восстановленного из конца отрезка t7, соответственно сим­вол hil{t2) - - точке пересечения кривой а с перпендикуляром из конца отрезка t7.

Результирующую кривую, являющуюся реакцией на периодиче­ское возмущение, обозначим у (t).

Введя условные обозначения, можно записать последовательность процедуры построения у (t):

y(ti)-hQ (*i);

У Wг)— ha (^з) (^г)і

У (^з) = (*з) hfj (t3);

y{Q = hM-hM + hM-

у (t*) = К (*s>) — К (h) + К (А>) — К (Q + ад (g и т. д.

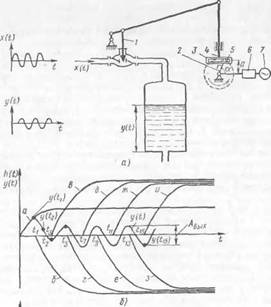
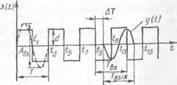
Рис. 13. Построение графика реакции системы на периодическое прямоуголь­ное возмущение;

а — пример определения частотной характеристики, б — построение графика реакции си­стемы. * — р изложен и* периодического сигнала, е—прямоугольное й сивусоид альное перио­дически е колеСанвя; 7 — регулирующий оріан. 2—кривошип, 3 — траверса, 4 — тяга, 5 — ползун, 6 — редуктор, 7 — электродвигатель

Соединив точки у (t), получим реакцию системы на периодические прямоугольные колебания у (£). Начальная часть у вплоть до t = t8 носит еще непериодический характер — неустановиьшиеся колеба­ния. Происходит это из-за несимметричности амплитуд первой а и второй б составляющих входного возмущения (рис. 13, в). После начальный переходный процесс затухает и устанавливаются периоди­чески повторяющиеся колебания с амплитудой А — установившиеся колебания. При дальнейшем построении частотных характеристик рассматриваются только установившиеся периодические колебания.

Перенесем один период графика выходного параметра у (t) (см. рис. 13, б) системы на график входных колебаний (рис. 13, г), соблю­дая масштаб времени. Сопоставляя периоды этих колебаний, мы убе­димся, что Твых — Твх, т. е. период сохранился. Но начало периода на выходе будет сдвинуто относительно начала периода входа на ве - личинуд Т. Причем выходное колебание отстает от входного вследст­вие инерционных свойств объекта. Следует обратить внимание на то, что выходные колебания имеют форму, близкую к синусоидальной.

Для снятия частотных характеристик применяют специальные приборы, генерирующие периодические колебания, — генераторы прямоугольных или синусоидальных периодических колебаний. Амп­литуды прямоугольных и синусоидальных колебаний должны быть связаны соотношением Ли — 1,27с/ при соблюдении этого условия реакция (выход) объекта будет одинаковая как на синусоидальное так и на прямоугольное периодическое возмущение.

Для изучения динамических свойств элементов системы опыт по снятию чаетотных характеристик повторяют многократно, изменяя период колебания Т.

Для рассматриваемого примера с уменьшением периода входных колебаний амплитуда выходных уменьшается, а отставание выходных колебаний во времени увеличивается