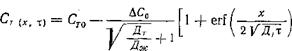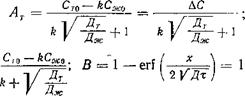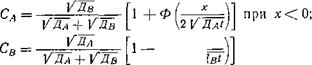Процесс взаимодействия твердой и жидкой металлических фаз при наплавке сопровождается той или иной степенью развития гетерогенной диффузии в зоне контакта. Составы фаз, находящихся в контакте, устанавливаются в соответствии с требованием равен­ства их химических потенциалов и даже незначительное время их сосуществования будет способствовать протеканию процессов гетерогенной диффузии в направлении установления фазового равновесия. Интенсивность протекания этих процессов опреде­ляется температурой, длительностью контактирования, градиентом концентраций и диффузионной подвижностью атомов.

Как уже отмечалось, практически полное подавление диффу­зионных процессов на границе раздела фаз может быть достигнуто лишь тогда, когда длительность контакта твердой и жидкой фаз не будет существенно превышать время ретардации хр. В подавля­ющем: большинстве случаев в реальных процессах наплавки время контактирования тк существенно больше, чем время ретардации процессов гетеродиффузии, Т. е. Хк > Хр.

С точки зрения развития процессов гетеродиффузии на границе раздела фаз, определяющей является стадия взаимодействия твердого металла с жидким. Развитие диффузионных процессов на стадии охлаждения закристаллизовавшегося металла в основ­ном определяется временем нахождения металла при повышенных температурах. Эта стадия представляет интерес в основном для элементов, обладающих большой диффузионной подвижностью, таких как С, 02, Н2 и др. Для большинства элементов замещения их; подвижность при переходе из жидкого состояния в твердое резко падает (коэффициенты диффузии уменьшаются на 3—5 по-

рядков) и длительность пребывания при повышенных температурах в реальных процессах наплавки оказывается недостаточной для существенного развития процессов химической неоднородности.

Одним из основных требований, предъявляемых к соединениям при наплавке, является получение соединений с высокими меха­ническими свойствами в зоне контакта и с минимальным разви­тием процесса растворения твердой фазы, приводящего к переходу элементов основного металла в металл наплавки. В большинстве случаев как наплавляемый металл, так и подложка являются сплавами и в связи с этим на свойства получаемых соединений также могут оказывать существенное влияние процессы гетеро-' диффузии примесей в зоне контакта.

В литературе имеются многочисленные сведения о влиянии раз­вития процессов химической неоднородности на физико-механиче­ские свойства соединений, в частности на механические, корро­зионные свойства, на поведение соединений при вибрационных испытаниях и т. д. [12, 56, 61, 70 и др.]. В работах [56, 61, 70, 75, 87] основном на примерах гетерогенной диффузии примеси элементов внедрения анализируется развитие химической неодно­родности в зонах сплавления илй перед движущимся фронтом кристаллизующегося металла. В связи с этим интересно проана­лизировать глубину и характер развития процессов химической неоднородности элементов замещения, составляющих основу взаимодействующих фаз, в зависимости от конкретных параметров процесса наплавки.

Количественное решение задачи по гетеродиффузии примеси в зоне контакта твердой и жидкой фаз при частных граничных

условиях приведено в работах Р. Иоста, Б. А. Мовчана и

Г. Л. Петрова [61, 70, 110]. Характер распределения примеси зависит от коэффициента распределения k, характеризующего различную растворимость элементов в твердой и жидкой фазах, от коэффициентов диффузии в твердой Дт и жидкой Цж фазах, продолжительности процесса т и градиента концентрации примеси на границе сплавления.

, Условия задачи диффузии примеси в двух средах при частных граничных условиях формулируются следующим образом:

1) .^£.т = д. д2с~ х<0' —— = Д —- д:>0-

1 dt dx2 ’ dt іЦж dx2 ’

2) Ст =* Сто при t = 0 и х <0; Сж = Сж0 при t = 0 и х > 0;

3) Ят о = (т)*-о на границе раздела ДЛЯ

всех t

0 оо

4) j (^Vo CT) dx = j (Сжо Сж) dx

—со 0

Q

5) = k в равновесном состоянии,

V

Решение имеет вид по [61, 70]

при я<0; (37)

где С, (ж, Х) и Сж(х. х) — концентрации элемента примеси соот-

ветственно в твердой и жидкой фазах в момент т > 0 на различных расстоя­ниях х (в см) от границы;

Ст0 и Сжо — начальные концентрации примеси в твер­дой и жидкой фазах (т = 0 тс);

Дт и Дж — коэффициенты диффузии примеси в твер­дой и жидкой фазах; k — коэффициент распределения; т — длительность процесса в сек.

Если градиент концентраций на границе сплавления при т = 0 отсутствует (наплавка, сварка однородного материала) — С0 = = Сж = Сто, уравнения принимают вид:

В том случае, если растворимость элемента в твердой и жидкой фазах одинакова (k = 1), возрастает роль градиента концентрации

на границе сплавления ДС„ = Ст0 — Сж0:

при л; < 0; (41)

В предельном случае, когда Дт ях Дж (отсутствует граница фаз, температура в металле постоянна), формулы преобразуются

в известные уравнения, применяемые для расчета ряда диффузион­ных процессов:

С(х, t) = Cio — l + erf(ПРИ *<°; (43)

Со (x, т) = Сп о + 1 ~~erf(2 )7лі) ПрИ Х>0' (44)

Значения коэффициентов диффузии Дт зависят от температуры, концентрации, структуры, примесей, напряженного состояния и могут меняться в широких пределах от 1 • 10-7 до 1 • Ю-16 см2 •сект1 и менее. Значения коэффициентов диффузии в жидкости в основ­ном лежат в пределах порядка 10~4—10-8 см2-сек-1.

Длительность контактирования в случае наплавки и сварки металлов меняется от 0,01—0,5 сек (смачивание) до 0,5—10 сек и более (наплавка, сварка) и зависит от погонной энергии и ско­рости сварки [14, 45, 70, 108].

Равновесный коэффициент распределения = в за­

висимости от легирующего элемента может быть больше или меньше единицы. Если примесь повышает температуру плавления сплава, то k0 > 1; если же происходит снижение температуры, то k0 <1. Для k0 < 1 ее значения обычно лежат в пределах от 1 до 0,001 (для систем, относящихся к чисто эвтектическим). В слу­чае kQ > 1 величина обычно принимает значения от 1 до 3, в ред­ких случаях (для бора в германии) k0 = 15 или даже больше. При наличии интенсивного перемешивания эффективные значения коэффициента распределения k могут сильно отличаться от рав­новесных и с увеличением интенсивности перемешивания стре­мятся к 1.

^0

k

(45)

где / — скорость роста твердой фазы; б — толщина ламинарного слоя; Дж — 10~6ч-10~4 см2-сек"1. Для большинства практических случаев неизвестны точные значения эффективного коэффициента распределения — k, коэф­фициентов диффузии Дт и Дж и длительность контактирования. Точное определение этих величин в реальных металлических системах связано с большими трудностями, так как их значения в значительной степени зависят от многочисленных побочных процессов. В связи с этим представляет большой интерес анализ уравнений (37) и (43) (с точки зрения определения влияния раз­личных переменных параметров k, Дт, Дж, т на точность получае­мых результатов.

В общем случае значения эффективного коэффициента распре­деления определяются из уравнения, полученного Бартоном и др.

Перепишем уравнения (37) и (38) в следующем виде:

(46)

(47)

где

х > 0; Д — Дт +ДЖ

д

Проанализируем изменение коэффициентов Ат, Аж и Б в урав­нениях (46) и (47) в зависимости от значений, принимаемых Ат, Аж, k и х.

Функция Ф (U) — интеграл вероятности — в зависимости от значений U меняется от 0 до 1. Практически Ф (U) равно еди­нице при U 2. Задавая различные значения л; в границах най­денных предельных значений диффузионной зоны, определяем соответствующее значение Ф (U) и В = 1 — Ф (U).

' Рассмотрим характер изменения множителя Ат в зависимости от значений, принимаемых коэффициентами k, Дт и Дж. Пусть числитель дроби АС0 = Ст — 1гСж0 — величина постоянная. Дж — для большинства металлов можно принять равным 5 • Ю-5 см2 - сект1. Как показывают расчеты, изменение величины коэффициента распределения (от 0,001 до 20) начинает оказывать влияние только при значениях коэффициентов диффузии в твердой фазе Дт > 10~8 см2-сек~1, т. е. в основном для элементов внедрения или элементов замещения при температуре, близкой к температуре плавления.

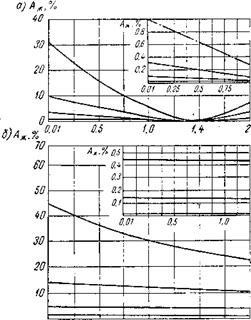
Оценим величину изменения множителя Аж на двух формаль­ных примерах, позволяющих более четко выявить характер изме­нения множителя Аж от k для различных зн°чений Дт. На рис. 25 представлена абсолютная величина изменения множителя Аж (в %) в зависимости от k для различных значений Дт, Сж0 и Ст0: на рис. 25, а —для Сж0 — 50%, а Ст0 = 70% (т. е. когда произведе­ние кСж достаточно велико) и на рис. 25, б — для Cj.0-^100%, Сжо —’ 0 (когда АС = Ст0 — Сж0—>100%, т. е. градиент концен­траций максимально велик). Рассмотрение этих случаев позволяет определить влияние коэффициента распределения на величину Аж. Приведенные данные показывают, что, начиная с коэффициентов диффузии Д = 10~8 см2-сек-1 и менее, изменение величины k в широких пределах, охватывающих почти все практические слу­чаи, не оказывает влияния на величину множителей Аж и Ат.

Таким образом, для большинства случаев диффузии элементов замещения величину эффективного коэффициента распределе­ния k можно не учитывать при решении гетерогенных задач с точ­ностью порядка 0,1—0,01%, т. е. в пределах точности локального

0.01

0.5

1

1.5

Рис. 25. Абсолютная величина изменения мно­жителя Ажв‘% в зависимости от fe для различ­ных значений, принимаемых DT, Сж и Ст: а — Сто—70%, Сж о = 50%; б С? о — 100%; Сжо = 0%

рентгеноспектрального микроанализа. В этих случаях для расчета можно пользоваться приближенными уравнениями: ЛС0

уж У Дж

СТ = С,

Дг

где

АС о — Ст о — С

Уравнения (37), (38) и (48), (49) для гетерогенной диффузии примеси неприменимы в случае контакта двух чистых разнородных

5 А. Е. Вайнерман и др.

-В

(48) (49)

то

і

Дж лс„

Сжо

■ В,

До»

ж 0-

65

металлов. В связи с этим рассмотрим задачу развития химической неоднородности в зоне контактирования твердой и жидкой фаз разнородных металлов. Пусть жидкий металл А (0 <Сх < +оо) находится в контакте с твердым металлом В (—оо <^х <0). Запишем уравнения для изменения концентрации в твердой и жид­ких фазах и уравнение, выражающее равенство потоков:

аасг дхг

Д

при л:<0; (50)

д[2]С.

= д

y при х>0; (51)

	/ / / 1 1 р	/		/	г X/ ' /
	1 / 1 / 1 1/	/		/
1	! "її 1 І ,2 U			is
.. Г 1 і И /	/1 s1n8		W // / у/
/ / /	/ / J

SO 40 20 П

0 1 2 3 4 5 6 Расстояние от границы спладления, мк

Рис. 26. Расчетные концентрационные кривые по (48) и (49) (/, 3, 4, 5, б) и экспериментальные (2, 7, 8), полу­ченные с помощью локального рентге­носпектрального анализа при контак­тировании жидкой меди со сталью для случаев:

1 и 2 — отсутствие диффузии; 3, 4, 8 — температура жидкой меди 1100° С, хк = — 0,5 сек 5, 6, 7 — температура жидкой меди 1400° С, хк = 1 сек

А,%о 100

= Дж(^)х=0 для всех t, (52) где СТ— концентрация эле­мента Л в В; Сж — концентрация эле­мента В в жидком металле А; Дт и Дж — соответственно ко­эффициенты диф­фузии элементов в твердой и жид­кой фазах. Выпишем граничные усло­вия:

Мт дх ) Х=0

дСг ~Ж дСж dt

ж дх-

(53) (54) (55) (56)

Ст + Сж = 1 при х = 0 для всех t Ст = 0 при t = 0 для х < 0;

Сж — 0 при t — 0 для л; > 0;

дСт дх

т = 0 при х = оо;

= 0 при х =—оо для всех І.

(57) (58)

1 + ф

2 Уд, і

1 — ф

2 УДжч.

Решение имеет вид: У Дж

С = _____ У Д, + УДж п УТт

УДу~г УДо,

при х<0; при х>> 0.

Уравнения гетерогенной диффузии примеси (37) и (38) и урав­нения (57) и (58) не учитывают наличия двухфазной области, изменения коэффициентов диффузии от концентрации. Сравнение расчетов с экспериментами приведено на рис. 26 (кривые 3 и 5 получены после пересчета кривых 4 и 6 с учетом влияния ко­нечных размеров эффективного фокального пятна микроанали­затора). Уравнения (57) и (58) могут быть использованы и при взаимодействии двух металлов в твердом состоянии. В этом слу­чае:

фЫщпр"х>0- (60)

(59)

(61)

где СА и Св — соответственно концентрации элемента А в В и В в А]

ДА и Дв — соответственно коэффициенты диффузии А в В и Б в Л.

В тех случаях, когда при соединении металлов необходимо свести к минимуму ширину зоны химической неоднородности, из

(37), (38), (57), (58) или (59), (60), задавая Ст, Сж или СА, Св

значение, равное 0, ах — значение ширины допустимой зоны гетеродиффузии, можно определить необходимые температуру и время процесса. При определении времени контактирования для соединения металлов в твердом состоянии необходимо учиты­вать дополнительное время, требуемое для достижения физичес­кого контакта на всем протяжении контактирующих поверхностей.

Период ретардации оценивается из уравнения (12). Одним из условий получения качественного соединения является ограни­чение длительности контактирования таким образом, чтобы не допустить образования интерметаллических соединений, т. е.

Ттс Ър ~f - Хд.

Расчеты, выполненные по уравнению ретардации (12) пока­зали, что время, вычисляемое по этому уравнению, всегда меньше длительности, необходимой для образования интерметаллидов в зоне контакта. Однако в связи с невозможностью в настоящее время точной оценки релаксации межфазной поверхностной энер­гии, время, вычисляемое из этого уравнения, по-видимому, су­щественно превышает истинное время ретардации тр, т. е. факти­чески из уравнения (12) определяется время х = хр + хд, а воз­можно и т = Хр + xd + V 3. В связи с этим возникла необходи­мость попытаться экспериментально определить тр и хр + - f т„. э и оценить энергию активации процессов гетеродиффузии в зоне контакта.

Для изучения вопросов регулирования тепловых и диффу­зионных процессов на границе раздела твердой и жидкой фаз В. С. Новосадовым, М. X. Шорошовым и Ю. Л. Красулиным была разработана специальная методика «жидкая клиновая проба», позволяющая за счет регулирования температуры и длительности контактирования фаз гибко регулировать процессы, протекающие в зоне контакта. Жидкий расплав в пробе заливается в клиновое пространство, ограниченное с одной стороны образцом (твердая фаза), а с другой стороны кристаллизатором из меди или другого материала с высокой теплопроводностью (сбоку клиновое про­странство с каждой стороны ограничено теплоизоляционными стенками). Регулирование длительности контактирования подлине образца осуществляется за счет разницы в скоростях и времени кристаллизации в верхней и нижней («капилляр») частях кли­нового пространства. В нижней части клина длительность кон­тактирования минимальная. Определяется она температурой по­догрева образца и заливаемой жидкости. .

Для устранения влияния газовой среды и с целью изуче­ния влияния состава среды на процессы, протекающие в зоне контакта твердой и жидкой фаз, клиновая проба помещалась в камеру специально сконструированной сверхвысоковакуумной установки, позволяющей производить исследования в контролируе­мой атмосфере: вакуум, окислительной, восстановительной и инерт­ной среде. В случае использования образца из диэлектрика (ситилл, керамика и т. д.) подогрев производился при помощи спе­циального нагревателя из молибдена, имеющего форму образца. В нижней съемной крышке высоковакуумной камеры преду­смотрена (при помощи сильфона и переходников) возможность приложения к образцу постоянного или знакопеременного сжи­мающего или растягивающего усилия для изучения влияния на­пряженного состояния на процессы, протекающие в зоне контакта. Для получения жидкого металла выбран способ бестигельной плавки металла во взвешенном состоянии в электромагнитном поле высокой частоты. Этот способ позволяет получать в течение

1— 2 мин жидкий металл высокой чистоты и однородности по составу (объемом до 2 cms) с различной температурой перегрева. Максимальная температура жидкого металла в индукторе типа «Лодочка» была порядка 2000° С.

Полученные образцы разрезались вдоль клиновой наплавки и в месте разреза делался шлиф, который анализировался на рент­геноспектральном микроанализаторе марки «Сатеса» Ms—46. Точность измерения методики «жидкая клиновая проба» лежит в пределах 10—15% и определяется точностью контактного спо­соба измерения температур и возможностями локального рент­геноспектрального анализа.

Выполненные исследования на различных парах разнородных металлов показали, что, изменяя температуру подложки и тем­пературу жидкого металла, можно гибко регулировать процессы, протекающие в зоне контакта, от интенсивного растворения твер­дой фазы, существенного развития процессов гетеродиффузии, образования интерметаллидов различного состава до практически полного подавления гетерогенной диффузии или отсутствия сма­чивания (обычная кристаллизация у твердой стенки). Длитель­ность контактирования может изменяться в широких пределах: от 0,08—0,1 сек до 3—8 сек и более. Большая разница в скоростях кристаллизации в различных частях клина позволяет рекомендо­вать использование пробы для изучения процессов, связанных с различной скоростью кристаллизации жидкости.

Одной из основных задач при исследовании по методике «жид­кая клиновая проба» была задача получения соединений с мини­мальным развитием процессов гетеродиффузии в зоне контакта и определение условий по температуре и времени, необходимых для получения таких соединений. Для этих исследований были выбраны пары Fe с Си (эвтектический тип диаграммы соединения с ограниченной, но конечной областью растворимости Си в Fe и отсутствием интерметаллидов) и пара Ті с А1, для которой ха­рактерна незначительная область твердых растворов со сто­роны А1 и имеется возможность образования интерметаллида типа ТіА13.

Результаты исследований при помощи локального рентгено­спектрального анализа (диаметр фокального пятна —2 мк) по­казали, что в обоих случаях, регулируя температуру подогрева образца и температуру перегрева жидкого металла, можно по­лучить соединения с глубиной зоны гетеродиффузии практически за пределами чувствительности рентгеновского метода,.

По литературным данным [13, 45, 70, 108 и др.] минимальные зоны, получаемые при различных способах соединения материа­лов, составляют 6—20 мк. Получение соединений с зоной гетеро­диффузии менее 1—2 мк представляет большой интерес, так как указывает на практическую возможность образования качествен­ного соединения при взаимодействии твердой и жидкой металли­ческих фаз с исчезающе малой величиной зоны развития хими­ческой неоднородности. Для получения таких соединений время процесса взаимодействия фаз не должно значительно превышать время, необходимое для протекания процессов смачивания..

Полученные экспериментальные данные по методике «жидкая клиновая проба» для различных металлических пар достаточно хорошо согласуются с расчетами по уравнению ретардации гетеро­диффузии (12). Время, определяемое по этому уравнению, ока­зывается всегда меньше времени, необходимого для образования интерметаллидов. Однако вследствие невозможности в настоящее время точного учета релаксации пика межфазной поверхностью энергии, длительность периода ретардации хр, вычисляемая по уравнению (12), оказывается существенно больше, чем время, определяемое экспериментально на клиновой пробе при исчеза­юще малой величине зоны гетеродиффузии.

Экспериментально определенная величина энергии активации гетеродиффузии (Еа), вычисляемая из уравнения (12), для соеди­нений с исчезающе малой величиной гетеродиффузии составляет Ea^s 29 ккаліг-атом для соединений Fe и Ni с Си, Еа ^ 22,4 ккаліг-атом. То же для соединений Fe с А1. Полу­ченные значения Еа существенно меньше, чем Еа — — -9г + в уравнении (12).

Эксперименты и расчеты показывают, что для получения со­единений с минимальным развитием гетеродиффузии длительность контактирования при температуре, несколько превышающей тем­пературу плавления, для пары Fe с А1 составляет при 700° С —4 сек, а для пар Fe и Ni с Си при 1100° С —0,5 сек.

Таким образом, уравнение ретардации (12) позволяет оценить условия процесса (температуру и время), необходимые для по­лучения качественного соединения (без образования интерметал­лоидов), а также при учете экспериментально определенных на клиновой пробе значений Еа получать соединения с исчезающе малой шириной зоны гетеродиффузии.

Конечные размеры эффективного фокального пятна рентгено­спектрального микроанализатора (в зависимости от анализируе­мых металлов порядка 2—4 мк) затрудняют анализ зон гетеро­диффузии шириной менее 5—10 мк. В связи с этим более точная оценка (тр) в настоящее время, к сожалению, не представляется возможной.

Проведенные исследования Показывают, что ширина зоны, измеряемая при локальном рентгеноспектральном микроанализе узких зон, равна истинной ширине зоны гетеродиффузии плюс диаметр эффективного фокального пятна. Таким образом, при анализе узких зон, для оценки действительной ширины зоны раз­вития химической неоднородности необходимо, оценив эффектив­ный диаметр электронного луча (излучающей области), вычесть его из ширины зоны, определяемой анализом.

В расчетах принималось, что температура процесса постоянна. В тех случаях, когда необходимо учесть изменение температуры в зоне контакта во времени, целесообразно использовать метод, предложенный в работе [70] для учета эффективной длительности контакта и коэффициентов диффузии.