При нулевом расходе рабочего тела аппроксимация одночленной формулой типа (8.28), естественно, неприемлема. В этом случае вид формулы может быть найден из соотношений (8.23), (8.24). При =

= 0 безразмерный параметр П^ = 0 и тогда выражение (8.24) при­нимает следующий вид:

(8.30)

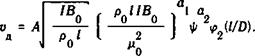
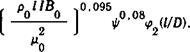С учетом значений показателей степени, определенных в предыдущем разделе,

Интересно сравнить значения скорости, полученные по формуле (8.31), со значениями скорости движения разряда между параллельными шинами (формула (3.3)). Функция <^(//Ь) при І/D ->

-> 0 (что соответствует случаю движения разряда между парал­лельными шинами) должна стремиться к единице и увеличиваться с ростом //D, поскольку при меньшем D при прочих равных условиях разряд набегает на среду с меньшей плотностью, что ведет к росту

скорости вращения v. Принимая ^ЛІ/D) = 1, из формулы (8.31) д *

получим

-.0,355^0,675 -0,325.-0,005/|в ч0,16 -0,19 /0 ооч

”.=" во 'о ' (Vo> “о ' (832)

Видно, что зависимости скорости вращения разряда, даваемые формулами (3.3) и (8.32), близки. Существенно отличается только зависимость от силы тока.

При использовании формулы (8.31) для обобщения экспериментальных данных и расчета скорости движения дугового разряда в плазмотронах коаксиальной схемы при условии нулевого расхода (правда, такой режим представляет интерес скорее при исследовании рабочего процесса в плазмотронах, чем в задачах генерации низкотемпературной плазмы) следует иметь в виду, что правильный результат может быть получен лишь для плазмотронов с достаточно длинным трактом истечения высокотемпературного газа. Если это условие не соблюдается и зона горения разряда отстоит недалеко от среза сопла плазмотрона (менее 30... 40 см), то вследствие эжектирования атмосферного воздуха в зоне горения разряда создаются условия, фактически не эквивалентные условию

Рис. 8.30. Зависимость

коэффициента А в формуле
(8.32) от индукции маг-
нитного поля (данные А. С.
Шаболтаса)

нулевого расхода рабочего тела, а эквивалентные вдуву в область разряда некоторого количества воздуха, тем большего, чем больше скорость вращения разряда. Справедливость этого положения иллюстрируется рис. 8.30, на котором приведены результаты

экспериментов А. С. Шаболтаса по исследованию скорости движения дугового разряда в коаксиальном плазмотроне при нулевом расходе рабочего тела. Из рис. 8.30 следует, что экспериментально

получаемый коэффициент А в формуле (8.31) при нулевом расходе рабочего тела тем меньше, чем больше магнитная индукция, т. е. скорость вращения как бы уменьшается с ростом магнитной индукции по сравнению с той, которая получалась бы при использовании формулы (8 31) с постоянным коэффициентом А. Это вполне понятно, если учесть, что при постоянном давлении скорость движения разряда сильно зависит от индукции магнитного поля, а следовательно, чем больше В, тем выше и эффект эжектирования атмосферного воздуха в зону горения разряда.

Следует заметить, что в плазмотронах большой мощности длина дуги относительно мала по сравнению с ее диаметром, и поэтому при переходе с одного режима на другой скорость движения дуги изменяется также за счет различного влияния концевых эффектов. Относительная длина дуги для исследованных плазмотронов менялась в

пределах / = 0,1...0,3 (размерности здесь такие же, как на рис.

3.12). Как видно из рис. 3.12, в этом диапазоне I коэффициент v в

зависимости скорости от определяющих параметров непостоянен, что приводит к изменению коэффициента А в формуле (8.31),

Итак, скорость вращения дугового разряда в плазмотронах с магнитной стабилизацией разряда может быть определена из критериального уравнения

где А' - численный множитель. По крайней мере в диапазоне изменения

безразмерного параметра П2 - P^v V{IB ) = 10 ...10 допустима

аппроксимация формулы (8.33) одночленной степенной зависимостью (8.29).

На основании экспериментов, выполненных на плазмотронах большой мощности с определением скорости вращения разряда, А = = 5,75-Ю-2.