В строгой постановке из-за высокой концентрации нагре­ва и существенной неравномерности температурного поля при сварке следует рассматривать трехмерную вадачу неизотерми­ческой пластичности. Математическая модель для трехмерной задачи рассматривалась в § 7.1. Учитывая зависимость в высо­кой степени затрат средств и времени для получения числовых результатов от мерности задачи, стараются отыскать пути для такой идеализации возмущающих факторов и геометрии сварного изделия, которая позволила бы свести трехмерную задачу к одномерной или, в крайнем случае, к двумерной. В каждом кон­кретном случае такой подход определяется целевым назначением расчета.

В главе 5 был рассмотрен упрощенный алгоритм решения задачи об одномерном напряженном состоянии в тонкостенных стержнях - полосах конечной жесткости с продольным сварным швом. Алгоритм ориентирован на применение ручного счета, по­этому были приняты существенные упрощения при описании физи­ческих процессов с целью получения числовых результатов при разумной затрате времени. Например, принималось, что отсут­ствует эффект ползучести материала и внешние силы, а ось шва совпадает с осью симметрии полосы.

Рассмотрим решение одномерной задачи в более общем и в то же ’’время формализованном виде, ориентированном на приме­нении вычислительных машин. Как и ранее, используем балоч­ные гипотезы, согласно которым:

1) сечения плоские и перпендикулярные к продольной оси до нагружения остаются таковыми и после нагружения;

2) влиянием поперечных деформаций на напряженное состоя­ние можно пренебречь (гипотеза о ненадавливании продольных волокон друг на друга).

Эти гипотезы справедливы для тонкостенных стержней,

Рис.7.6. Схема тонкостенного
стержня

толщина элемента относительно мала, мощность источника теплоты достаточно велики.

Рассмотрим прямолинейный тонкостенный стержень-балку произвольного сечения, свободную от закрепления с продольным швом (рис.7.6). Пусть стержень подвергается внешней нагрузке силе Рх и моментам и, в общем случае переменны­ми во времени. Согласно гипотезе плоских сечений уравнение продольной деформации в приращениях без учета кручения можно записать аналогично уравнению (2.25)

где, ЛС* - приращения кривизны осевой линии стержня в плоскостях хОа, и хОу соответственно.

Основное уравнение, связывающее приращение деформации ех и напряжения получаем из первого уравнения (7.27)

при

1 (7.40)

йш+к і 2. 2

где - относительно напряжения бх, получим

или с учетом (7.39)

[асх-дсггл^-л£т^) ] ■ <7*42)

При отсутствии пластичности и ползучести (у>,= l/E = const) уравнение (7.41) принимает привычный вид закона Гука в при­

ращениях

6>х-б£=Е(Л£.х--Дет) (7.43)

ИЛИ

ЛбяГЕйе® . (7.44)

Неизвестные величины Де. Хо14Су, АСг определяются из уравнений равновесия при текущем значении линеаризованной задачи

^х(у, г>^<1г,= Му

где принимается из уравнения (7.42).

Физическая нелинейность в уравнении связи (7.40) реали­зуется с помощью итерационного процесса (см. 7.2.1). Измене­ние функции состояния материала у, на текущей итерации (п) происходит в зависимости от состояния материала на предыдущей итерации ( п - К ):

I) уГ = Р<рГ°+«'Р>[г + Д tj, если 16х °|<63(Т);

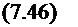2) fin1=y>r° , если |б£ Л|-6вЮ ;

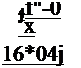(л) (п-0

3) у, = у<

Первый вариант соответствует упругому нагружению или разгрузке; второй - нейтральному нагружению, когда пластиче­ские деформации не изменяются и не происходит разгрузки, третий - пластическому деформированию. Все обозначения соот­ветствуют формулам (7,37) и (7,38).

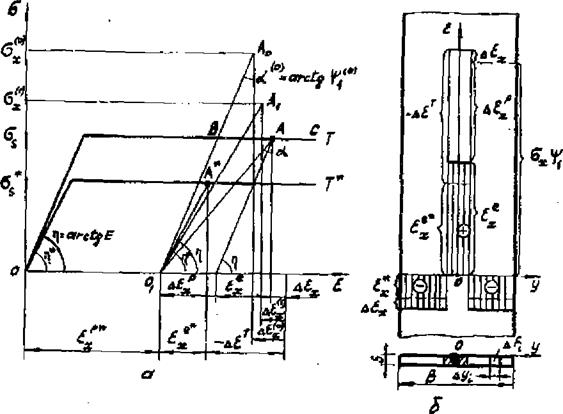
Рис,7.7, Расчет деформации шва при охлаждении

Рассмотрим приведенный итерационный процесс подробнее на примере сварного стыкового соединения. Для простоты при­мем, что ось шва и продольная ось симметрии совпадают, а внешняя нагрузка отсутствует (рис,7,7,б).

Выберем одно из центральных поперечных сечений сварной конструкции и его площадь Л* с шагом (или ) разо­бьем на элементарные площади (или ).

Назовем зти элементарные площади ячейками. Далее разобьем весь период нагрева и охлаждения сечения на интервалы (этапы нагружения). Положим, что заданы начальные условия и извест­на температура и свойства материала в центре каждой ячейки на всех этапах (температурное поле можно найти аналитически или численным методом при той же разбивке; см. § 3.7). По­следовательно решим задачу на заданных этапах, начиная с пер­вого. Пусть известно решение задачи на этапе (t-2flt, t-frt ). Требуется найти решение на этапе (t-bt, t), когда шов ох­лаждается.

Пусть температура заданной точки (ячейки) на оси шва в предыдущий момент равна Т* , а ее состояние на кривой

деформирования 640 характеризуется точкой А* (рис.7,7,а), т. е. после затвердевания в шве накопились пластические де­формации е^* , равные отрезку 00, , и упругие деформации

&х. При этом напряжение равно пределу текучести, 6Х =

= 6* = , Схематизированные эпюры деформаций в попе­

речном сечении полосы, разбитом на три ячейки, показаны на рио.7.7,6.

Пусть через время At температура шва уменьшилась до Т, что вызвало дополнительную температурную деформацию й£т,

а также повышение предела текучести 6S и модуля упругости Е. При этом теоретически возможна следующая кинетика

напряженно-деформированного состояния шва:

1) разгрузка, и тогда точка А, характеризующая состоя­ние шва, переместится на отрезок 0,В(£Х=£Х*') ^

*

2) нагрузка, и тогда точка А переместится на отрезок ВСГе^е^ •,

3) нейтральное нагружение, и тогда точна А переместит­ся в точку Б (ех=Ех* и 6^=6^.

Заранее указать кинетику состояния заданной точки мы не можем.

Предположим, что заданная и все остальные ячейки дефор­мируются упруго, т. е. в исходном приближении всюду примем

|/Е(Т) . Для любой і - й ячейки при отсутствии изгиба согласно (7.42) можно записать

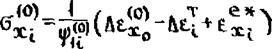(7.48)

Подставляя (7.48) в первое уравнение (7.45) и заменяя интеграл конечной суммой, получим

Решив это уравнение относительно и подставляя

значение в уравнение (7.48), получим распределение

продольных напряжений 6Х. , соответствующее начальному рас­

пределению функции состояния материала. Если рост пре­дела текучести металла шва при охлаждении не может скомпен­
сировать роста напряжений из-за температурных деформаций, то расчетные напряжения оказываются выше допустимых:

(в противном случае точка (к была бы на отрезке 0<Б ). По­этому значения корректируются по формулам (7.46) и

при новых значениях определяют приращения полных де­

формаций ЛЕ-хо и напряжения при первом приближении Эта процедура повторяется до тех пор, пока функция в

каждой ячейке практически перестанет изменяться (см. усло­вие (7.47) . Полученное предельное состояние и будет решени­ем задачи в конце рассматриваемого этапа t. Состояние ме - тепла шва определяется точкой Л (рис.7.7,а).

Нетрудно определить приращение пластических fie., пол­ных &ех деформаций и упругие деформации (рис.7.7,а).

Эти данные используются в качестве исходных для расчета де­формаций и напряжений на следующем этапе нагружения t+fit.

Рассматривая последовательно напряженно-деформированное состояние выбранного сечения во времени (на всех этапах нагружения), получим в итоге остаточные напряжения и дефор­мации.

Если шов не совпадает с продольной осью (см. рис.7.6), то на каждой итерации следует определять йех0 , , ЛСг из

трех уравнений (7.45), заменяя интегралы конечными суммами.

Изложенный численный метод определения сварочных дефор­маций и напряжений представлен на рис.7.8 в виде общей блок - схемы. В качестве исходных данных в вычислительную машину вводится информация о геометрии сечения сварной конструкции, свойствах материала, внешней нагрузке, режимах сварки, раз­бивке сварочного цикла на этапы и т. п. В качестве результа­тов могут выводиться распределения напряжений, упругих и пластических деформаций, характеристики общих сварочных де­формаций (£х0 ,СуЛг.) на кажД°« этапе и т. п.

Приведенный алгоритм решения задачи об одномерном на­пряженном состоянии сварной конструкции не является единст­венным. В 40-х годах Н. О.Окербломом был предложен числен­ный метод, ориентированный на применение ручного счета и на­званный им графо-аналитическим. Этот метод можно достаточно просто реализовать на вычислительных машинах.

Рис.7.8. Блок-схема программы, реализующей численный метод определения одномерного напряженного состояния

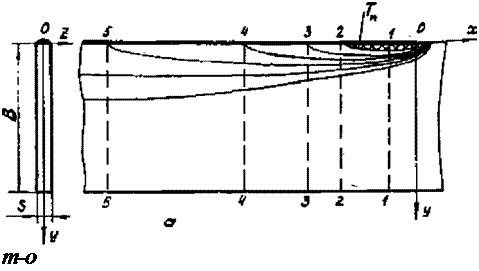
Физический смысл метода Окерблома легко прослеживается. Рассмотрим его подробнее на примере наплавки валика на про­дольную кромку полосы (рис.7.9,а). Будем полагать, что мате­риал полосы идеально упругопластический, модуль упругости Е не зависит от температуры, эффект ползучести, деформации при

фазовых пре­вращениях и внешние силы отсутствуют.

Эти допущения не являются принципиальны­ми, они приня­ты только для упрощения и облегчения ана­лиза физиче­ской картины.

Выберем одно из цент­ральных попе­речных сечений - полосы. Если полоса доста­точна длинна, то ее концевые участки не-бу­дут оказывать влияния на развитие деформаций и напряжений в удаленных от концов центральных сечениях. Центральное сече­ние неподвижной полосы в разные моменты будут находиться в различном положении относительно подвижного источника тепло­ты, например в положении 1-І, 2-2 и т. д, (рис.7.9,а), и тог­да рассмотрение напряжений и деформаций в данном сечении во времени можно заменить последовательным рассмотрением напря­жений и деформаций в данный момент в поперечных сечениях, удаленных на различное расстояние от источника теплоты.

Рассмотрим деформированное состояние выбранного сечения в некоторый момент t. Проинтегрировав последовательно уравнение

x

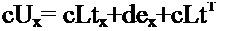на отрезке 0, t-at и t-ftt, t, получим

t

t-At

где (dtx/dt)dt - накопленная пластическая деформа-

tt f

ция в момент t-ftt (на предыдущих этапах); Hx=UcUx/dt)dt -

t'At

приращение пластической деформации в интервале ftt (на те-

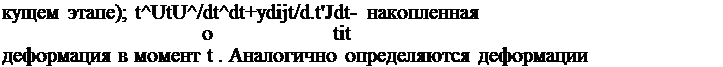pt-ftt.. - t

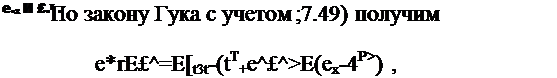полная

где ££ =е. т+ tpx +йер.= ет + - сумма температурных

и пластических деформаций в текущий момент t.

если отсутствуют внешние силы, то напряжения по сечению взаимно уравновешены:

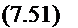
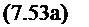
I) JdxdF = 0 І 2) ^6x}dF=0.

F F

Подставляя выражение (7.50) в (7.51), получим О (£x-£x)EdF=Es(^xcbj4eT^dy1) = 0 ,

pJ Б Б

так как Е=const и dF=s&^ . Отсюда

1) ^«d^tjd} .

Ъ Ь

Аналогично получим второе уравнение

2) ^уехсЦ = ^£хрсЦ.

ь

Обозначим

(7.54)

и перепишем уравнения (7.53) в виде

I' = ; 2) y£xd} = MTp

ъ ъ

Из последних уравнений можно найти два любых параметра

прямой полных деформаций £х(у) , например при ^=0 и ее значення £Х((У) и ех(Ъ) . Подставляя уравнение прямой £Х(У) ♦ проходящей через две точки £х(0) и, в урав­

нения равновесия (7.55) и решая их, получим

При выводе формул мы полагали, что известны величины FTp и Мтр, т. е. известно распределение (суммы

£ + + Д£Р, )., включая приращения пластических деформаций

на текущем этапе нагружения й£х (см. уравнения (7.54) . Од­нако эти величины й£х зависят от текущего распределения

общих деформаций (от и £x(S) ). Полученную таким

образом нелинейную систему уравнений (7.56) можно решить с заданной точностью методом итераций:

cm,.. }

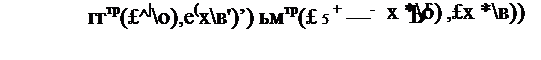£х(0)=------------ 5--------------------------- , -

где (п1) , - номера итераций. За начальное приближение

при t=0 можно принять, например, условие £х (0)=£Х'Б,) = 0 .

Таким образом, решение задачи о напряженно-деформирован­ном состоянии на текущем этапе нагружения сводится к решению системы нелинейных уравнений (7.57). Практика показывает, что итерационный процесс является устойчивым и достаточно быстросходящимся.

Рассмотрим кинетику деформаций выбранного сечения.

Сечение в положении 1-І (см. рис.7.9,а) характерно тем, что оно пересекает изотерму Тж в точке ее максимальной ши­рины и поэтому является граничным сечением, в котором все волокна при температуре Тп. т* нагреваются. Е период нагрева материала сечения развиваются пластические деформации одного

знака (пластические деформации укорочения), что - соответст­вует нагружению, близкому к простому. Поэтому накопленные пластические деформации в сечении в положении 1-І можно оп­ределить, рассматривая его только в данный момент t, . При­мем этот момент завершающим первый этап нагружения сечения. Последующие этапы пусть определяются моментами,

когда сечение находится в положении 2-2, 3-3 и т. д.

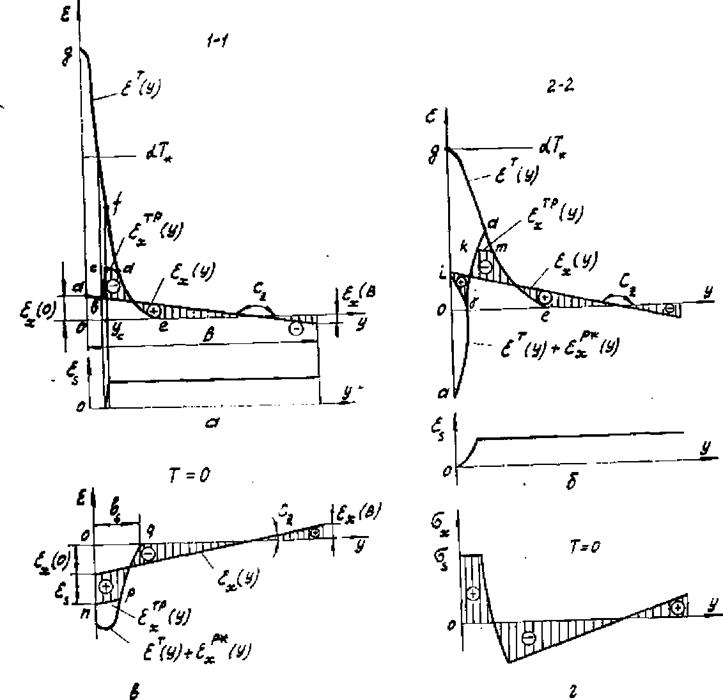
Рис.7.10. Кинетика продольных деформаций (а, б, в) и напряжений (г) в поперечном сечении полосы при наплавке валика на ее продольную кромку

На рис.7.10,а показано распределение деформаций в сече­нии в момент, когда оно находится в положении 1-Х: тем­пературних «•ТМ К ПОЛНЫХ. Разность Е-х (У) И

согласно уравнению (7.49) равна сумме упругих и

приращения пластических деформаций е^.+йе^ (здесь e£So,

так как деформации перед наплавкой отсутствовали). Распреде­ление выделенных из этой суммы упругих деформаций е.|.(у) по­казано вертикальной штриховкой. Распределение максимально возможных значений упругих деформаций ts(y) показано внизу

на рис.7.10,а, оно построено по зависимостям бї(Т') и T(f) .

В зоне шириной " координата точки $ ), где Т>Т*

напряжение и упругие деформации отсутствуют из-за высокой температуры (tb=0 ); в ней имеются только пластические де­формации. Распределение приращения пластических деформаций

укорочения характеризуется фигурой abcdSg. Напри­

мер, в волокне имеются как пластические деформации уко­рочения, так и упругие деформации укорочения, равные. Алгебраическая сумма температурных и пластических деформаций представляет собой кривую abc. de, следо­

вательно FTp равно площади фигуры abode0 сі.

Аналогично определяем деформации сечения в момент, когда оно находится в положении 2-2 (рис.7.10,б). Из разно­сти а. х(У) и £т+ерГ (кривая ajxdme ) выделяем упругие де­формации, максимально возможные значения которых определяют­ся кривой ц(У) , и приращения пластических деформаций в интервале, которые характеризуются фигурами KdmK

(деформации укорочения) и tjai (деформации удлинения). Вид­но, что зона пластических деформаций расширилась ( ут>у& )• Итак, накопленные пластические деформации укорочения е.^ в сечении в момент tz характеризуются ijKmdgi. , а FTp и Мтр определяются фигурой ijKmeOi. .

Таким образом, по распределению пластических деформаций в предыдущий момент определяется деформационное состояние в последующий момент. Распределение остаточных деформаций, когда Щ* О, показано на рис.7.10,в. Вблизи ()|<Ур) вплоть до полного остывания происходят пластические деформации уд­линения, хотя остаточные пластические деформации - деформа­ции укорочения. В этой зоне упругие деформации удлинения и растягивающие напряжения максимальны. На границе пластиче­ской зоны шириной bs максимальны упругие деформации укоро­чения и сжимающие напряжения. Видно, что остаточная кривизна изогнутой продольной оси по знаку обратна кривизне Са при нагреве.

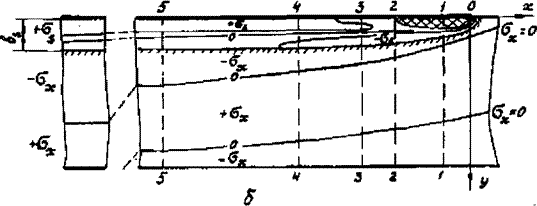
По распределению остаточных упругих деформаций в сече­нии построена эпюра остаточных продольных напряжений бх (рис.7.Ю, г). Эпюра напряжений в сечении в рассматриваемые моменты позволяет построить поле временных напряжений в по­лосе. На рис.7,9,6 приведена граница сжимающих и растягиваю­щих напряжений (линии бх= 0) и граница зон, где напряжения достигают предела текучести при начальной температуре (ли­нии бх=іб5 ).

При изложении численного метода Окерблома мы для про­стоты пользовались допущениями, которые, вообще говоря, не являются обязательными. Как и в других численных методах, можно было дополнительно учитывать следующие факторы:

1) упрочнение материала при пластическом деформировании, для чего в условии развития пластических деформаций мгновен­ный предел текучести следует определять с учетом накопленных пластических деформаций, 6%=6s(T, e^') ;

2) температурную зависимость модуля упругости Е, для чего в уравнениях равновесия (7.52) при интегрировании учи­тывать переменность модуля по сечению, Е(у) ;

3) фазовые превращения, для чего под величиной следует понимать сумму температурных и фазовых деформаций;

4) ползучесть, что учитывается в выражении (7.50) так же, как и мгновенная пластичность;

5) разнородность свойств металла шва, околошовной зоны

и основного металла, что учитывается при определении текущих зависимостей и Е(у) ;

6) начальные пластические деформации, вызываемые пред­шествующей сваркой, прокаткой и т. п., для чего принимать на первом этапе начальные пластические деформации Ер*(у)' отлич­ными от нуля;

7) ограничения на продольные деформации (разного рода закрепления полосы), что учитывается заданием уравнения пол­ных деформаций ех(У) ;

8) заданную во времени внешнюю нагрузку в виде про­дольной силы P(t") и изгибающего момента Mlt) и учиты­вать их, начиная с уравнения (7.51).

Изложенные алгоритмы численного решения задачи об одно­мерном напряженном состоянии позволяют проследить за кине -

гиг

тикой сварочных деформаций и напряжений при последовательном выполнении продольных швов в стержнях-балках таврового, дву­таврового, коробчатого и другого сечения. Естественно, тогда необходимо следить за температурным полем во всем сечении и учитывать изгиб в двух плоскостях.

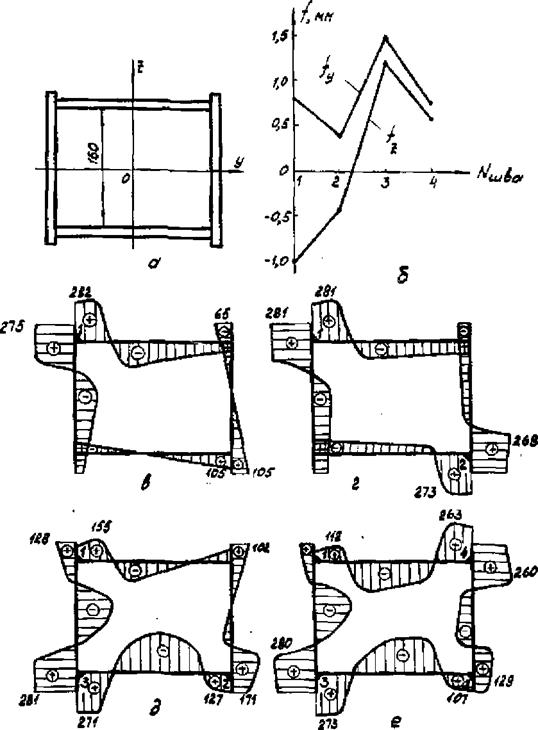
Рис.7.II. Схема сечения балки (а), стрелка прогиба продольной оси на длине 2 м (б) и распределение про­дольных напряжений <5х (МПа) после выполнения перво­го (в), второго (г), третьего (д) и четвертого (е) швов

Сварные балки коробчатого сечения находят широкое рас­пространение в промышленности. Рассмотрим в качестве примера балку, собранную из четырех одинаковых полос сечением 10x200 мм (рис.7.II, а). Материал - низкоуглеродистая сталь, модуль

.упругости Ё = 20 ГПа$ предел текучести 6S = 280 МПа при тешературе Т = 0°С. Режим сварки с^п= 1540 кДж/м.

Из рис.7.10,в-е видно, что значительная жесткость балки обусловливает высокий уровень продольных напряжений при выполнении продольных швов. Остаточные напряжения макси­мальны в зоне последних швов (3-го и 4-го). При остывании этих швов происходит продольное укорочение балки с изгибом вокруг оси, близко проходящей через швы I и 2. Поэтому швы 3 и 4 частично разгружают ранее выполненные швы I и 2. Сложное взаимное влияние швов приводит к значительной кривизне балки (рис.7.11,6), хотя швы расположены взаимно симметрично и вы­полняются на одном и том же режиме.

Можно отметить, что исследованию изгибных деформаций стержней-балок посвящено довольно много работ, что объясня­ется важностью проблемы и в то же время относительной про­стотой расчетной схемы и экспериментальных методик определе­ния общих деформаций.