7.4.1. Плоское напряженное состояние

При сварке относительно тонкой пластины температурное поле по толщине близко к равномерному, а ширина зоны пласти­ческих деформаций больше толщины пластины. Тогда напряженное состояние определяется Только компонентами 6Х, бу И и называется плоским напряженным состоянием. При этом пред­полагается, что эти три компоненты не зависят ОТ 7L, т. е. не меняются по толщине, а являются функциями ТОЛЬКО ОТ I и

1 •

Найдем уравнения связи приращения деформаций с напря­жениями. Подставляя значения 6ь=г^г=ггл=0 в уравнения (7.27), получим

г. ф+ку к-ф. о 5 і

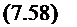- К-Ф. І *

-- °У + £у 1

(7.59)

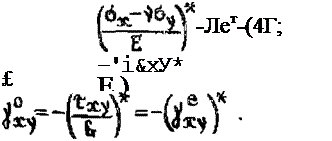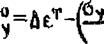
Уравнения связи в матричной форме имеют вид

Решая уравнение (7.60) относительно напряжений! умножая его слева на иатрицу [D] , получим

Ножно отметить, что яри наличии только упругих дефор­маций (у ■ і/г. От ) и начальных деформаций в виде температур­ных иа уравнения (7.61) получается известное уравнение тео­рии упругооти, связывающее напряжение и деформации за весь период нагружения

Условие з?«йучести определяется соотношением пределе, текучести й6(Т) ш интенсивности напряжений dj.. £7*12). При плоском напряженном состоянии

Присоединив условия на контуре пластины, формально по­лучим задачу термоупругости на некотором этапе нагружения пластины и некотором приближении по f. Метод решения этой задачи будет рассмотрен в подпараграфе 7.4.4.