Универсальные математические модели рекуперативных теплообменных аппаратов
 4 мая, 2013
4 мая, 2013  admin
admin Рекуперативные теплообменные аппараты представляют собой систему, в которой перенос энергии (тепла) от одного теплоносителя к другому осуществляется при их постоянном взаимодействии через разделительные стенки. Универсальную математическую модель такого аппарата при ламинарном режиме течения обоих теплоносителей запишем в риде системы уравнений — переноса количества движения, сплошности, переноса энергии (тепла) и переноса тепла в твердом теле:
TOC o "1-5" h z Л»!- дР, / 1
Р»-ЗГ = ~-й7 + 1Ч [у^|*+з4у»|) + р|£„
<ко, дР, ( 1
Р1 "2Г = — !£■ + и +-3 «Иув»!] + Р1&,
СЬ>,, дР, I т
91~ЗГ =------- еГ + ^1 (у2“*!* + у Луи»!] + Р]£г. (1.9)
1 <IР, дш1х диа1и ди>1г
Р1 ' дх ' ду дг ’
Дш2х дР2 / 1.
Рг-^т- = —17 + + у с11Уаи2] + №х,
ДР2 [ I.
Р*-а? = —а£ + № [ч^ау + у + ?2Яв,
Йи2, дР2 / I
Рг~£Г = — -%■ + Иг (У2^2г + у <11V ш2] + Ыг>
= 0;
1 <*Р2 . &>2х ^2у. ^гг
Р2 а* ' дх ' ду ' дг
TOC o "1-5" h z. _ д11 , . Га(сР1Р|®1*) , Чср^х^у) , ^Р,®,*)] , срР1 *- + и [ Тх + Ту + Тг ] +
Г дл д/. 3<,1 а Эм зг, й &1.
+ ср1?1^х-¥х+ш1уТу +и>ч-д-г = д;11Тх + Ту Ту + ^'д!1
. . д12 , , (д{Ср2?2™2х) , НСр2^2и) , д (СР2?Р>2г)] ,
СР2?2 Тх + (2 [--------- Гх------ + -------- Ту------- + --------- Тг------ ] +
Г д*2 , д{2 , Й<2] д &2 д д12 ,д. Щ
+ СР2Р2 [и>2х Тх + ^Ту + а>2гТг - Тх12Тх + Ту12Ту + ТгХ2 д!' дв __ д. Э0 д дв д дв СртРт дг дх ^ дх'ду т ду ' дг 7 дг'
Здесь Ри Р2 — давление в каналах первого и второго теплоносителей; иих, Х2)у, тг — проекции вектора скорости потока первого и второго теплоносителей (обозначены индексами 1, 2); /1, /2 — температура в каналах первого и второго теплоносителей;^, цу, gг—проекции ускорения свободного падения тепла; 6 — температура разделительной стенки; р1, р2, рт— плотность первого и второго теплоносителей и разделительной стенки соответственно; ср 1, сР2, сщ — удельные теплоемкости первого, второго теплоносителей и разделительной стенки соответственно; Х|, л2, Хт— коэффициенты теплопроводности первого, второго теплоносителей и разделительной стенки; щ, р.2— динамическая вязкость первого и второго теплоносителей.
Плотности теплоносителей обычно существенно зависят от давления и температуры, поэтому к системе уравнений (1.9) необходимо присоединить уравнения состояния теплоносителей
Р1*=/(Р|, *0; Р2 = /(Ра, /а). (1-10)
Таким образом находим систему тринадцати уравнений с тринадцатью неизвестными: шц, и>и, хи2х, и>2у, ш2г, t, 72, 9, Р, Рг, Рь Р2*
Для получения единственного решения необходимо к системе (1.9) — (1.10) присоединить краевые условия. Однако решение задачи об определении распределения скоростей, давлений и температур в теплоносителях и температуры в твердом теле даже для простейшего теплообменного аппарата в форме прямоугольных каналов в случае ламинарного режима течения теплоносителей сопряжено со значительными техническими и математическими, трудностями.
Вместе с тем, создавая теплообменные аппараты, мы стремимся к компактным конструктивным решениям. Ясно, что компактность теплообменного аппарата требует максимальной интенсификации процессов энергопереноса от одного теплоносителя к твердому телу и от твердого тела к другому теплоносителю. Ввиду того что интенсификация процессов энергообмена связана с турбулизацией течений, уравнения Навье — Стокса должны быть записаны для турбулентного потока [51}
Благодаря развитию за последнее десятилетие теории пограничного слоя н турбулентного переноса открываются широкие возможности построения универсальных математических моделей рекуперативных теплообменных аппаратов. Однако и сегодня решение сопряженных задач, к которым относятся и названные модели, связано с преодолением принципиальных математических трудностей. Поэтому современные подходы к созданию математических моделей теплообменных аппаратов базируются на расчленении задач течения и переноса энергии (тепла).
Разрывая связь между влиянием сил вязкости на распределение скоростей в потоке (и прежде всего в пограничном слое) и на теплообмен между теплоносителем и твердым телом, мы вводим некоторый коэффициент, определяющий условие равенства потока тепла, отданного движущимся теплоносителем и воспринятого твердым телом. Указанный коэффициент называется коэффициентом теплоотдачи. Он определяет значение теплового потока от теплоносителя к твердому телу (или наоборот), отпссснногок единице поверхности, при разности между температурой поверхности твердого тела и некоторой характерной температурой набегающего потока в один градус.
Таким образом, сложность теоретических и технических проблем совместного решения системы уравнений (1.9) — (1.10) заменяется проблемами отыскания эмпирических связей коэффициента теплоотдачи в каналах различной геометрии при разных фазовых состояниях теплоносителей с определяющими параметрами (критериями) в форме корреляционно-статических уравнений множественной регрессии. Последнее означает, что при изменении формы каналов теплообмениого аппарата, введении турбулизаторов потока различного типа, а также при различных фазовых состояниях теплоносителя мы всякий раз па основании обработки специально организованного эксперимента определяем уравнения параметра состояния, т. е. коэффициента теплоотдачи, обычно в форме N11=/ (1?е, Рг, ...).
Отмеченное обстоятельство привело к развитию экспериментальных методов исследования механизмов теплопереноса, когда все проблемы сложных процессов течения и энергообмепа изучались па основе методов физического моделирования и обобщались эмпирическими уравнениями теплообмена. В некоторых сравнительно простых схемах течения, решая уравнения пограничного слоя, получают зависимости коэффициента теплоотдачи от определяющих переменных и теоретически. В таком случае обычно полагают, что условия на стенке (твердом теле) заданы и постоянны.
Введя понятие коэффициента теплоотдачи и установив таким образом условия теплового взаимодействия потоков теплоносителей и твердого тела, а также приняв распределение скоростей, полученное в результате решения задачи течения для случая И
неизменности теплофизических характеристик сРі, рі, ср2 рг и установившегося режима течения в канале, математическую модель переноса тепла в рекуперативном теплообменном аппарате получим в виде системы уравнений энергии:
|
Дх дх' ду ду ' дг дг' |
(1.11)
|
Д, дІ2 . д. й2 , а. д(2. |
![]()
|
Дх 2 дх^ ду 2 ду ' дг дг' |
![]() (1.12)
(1.12)
(1.13)
Здесь и>х, ха1у, хюи, Щг — проекции вектора скорости
Одного и второго теплоносителей, полученные в результате решения гидродинамической задачи или экспериментально.
Для решения задачи о распределении температур в потоках теплоносителей и разделительной стенке к системе уравнений (1.11) — (1-13) необходимо присоединить краевые условия.
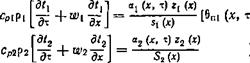
|
Т — д 90 _і_ д 02. Сртрт ^ — дх Ь-т дх + ду ду- |
![]()
|
[і2(х, т)— т)1; (1.15) |
![]()
|
(1.16) |
![]()
|
І{х, 0) = і4 (я); Ь{х, 0) = £(*); 0(л:, у, 0) = й{х, у). (1.19) Дв (х, у/,, т) <*г(х, - с) [^2 (>с, *)— впг(х, *)1 = Хт--- ^----- : (1.18) |
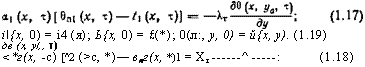
|
Присоединим к системе уравнений (1.14) — (1.16) краевые условия, которые определяют тепловое взаимодействие потоков с твердым телом, а также начальное распределение температур в потоках и твердом теле: Такие модели переноса тепла применимы для анализа работы рекуперативных теплообменных аппаратов, в которых необходимо учитывать временное запаздывание в изменении |
 В большинстве современных рекуперативных теплообменных аппаратов течение в каналах может рассматриваться как одномерное, поэтому математическая модель переноса тепла принимает вид
В большинстве современных рекуперативных теплообменных аппаратов течение в каналах может рассматриваться как одномерное, поэтому математическая модель переноса тепла принимает вид
температуры второго теплоносителя вследствие тепловой емкости разделительных стенок. Это особенно важно при изучении динамики переходных процессов работы теплообменных аппаратов и разработке систем автоматического управления теплоиспользующим оборудованием.
Если пренебречь количеством тепла, заключенным в разделительных стенках, и его изменениями в нестационарных процессах, то энергетическую модель рекуперативного теплообменного аппарата можно получить, введя понятие коэффициента теплопередачи к. Известно, что коэффициент теплопередачи определяет условия равенства тепловых потоков между двумя теплоносителями с учетом термического сопротивления разделяющих их стенок и коэффициентов теплоотдачи на поверхностях твердого тела, взаимодействующего с потоками теплоносителей.
В этом случае математическая модель переноса тепла в рекуперативном теплообменном аппарате при одномерном течении теплоносителей будет описываться уравнениями энергии
Cp.Pi {х) ib (х, - о-м*. 01; (1-20)
СРт [^2 + w2x Щ = k (х^{*{х) [<, (X, x)-i2(x, Т)|. (1.21)
При. начальных условиях t(x, 0) = А (х) (1.22); t2(x, 0) = = В{х) (1.23). Решение системы уравнений (1.20) — (1.21) при начальных условиях (1.22), (1.23) может быть получено на цифровых ЭВМ и на аналоговых вычислительных машинах (АВМ).
Поскольку современные рекуперативные теплообменные аппараты представляют собой структуры со сложными течениями одного теплоносителя относительно другого, модели типа (1.14) —
(1.19) , (1.20) — (1.23) могут быть использованы как модели модульных элементов. Детально вопросы применения машинных методов расчета рассмотрены в гл. 5.

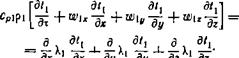
 Опубликовано в
Опубликовано в