Формулы, которые мы представили для исчисления ставки по векселям и дохода по ценным бумагам, служат для вычисления нормы прибыли, приносимой ценной бумагой при заданных цене-и сроке погашения. Существуют также важные формулы для вычисления цены или текущей стоимости ценной бумаги. Какую цену, например, вы согласитесь уплатить за облигацию номиналом 1000 долларов, с купонной ставкой 8% и сроком погашения 12 лет! Что определяет цену, которую вы платите за акцию корпорации?

Текущая стоимость ценной бумаги со сроком погашения в 1 год

Рассмотрим для начала очень простой случай,— текущую стоимость ценной бумаги, погашаемой через год без всяких процентных платежей. Уравнение 3.4 — это формула текущей стоимости такой ценной бумаги:

Р_-

1 + і'

ГдеР — текущая стоимость, М — стоимость на момент погашения; і — ставка процента в виде десятичной дроби. Эта формула выводится из основных характеристик одногодичного займа — количество денег, выплачиваемое при погашении, равно произведению занятых денег на сумму единицы и процента, выраженного десятичной дробью, Как показывает уравнение 3.4, количество денег, которое потенциальные покупатели могут заплатить за обещание выплатить им обратно некоторую сумму денег через год (т. е. стоимость на момент погашения), зависит от нормы процента. Поэтому покупатель поинтересуется процентными ставками аналогичных ценных бумаг с таким же кредитным риском. Если средняя ставка по таким ценным бумагам равна, например, 8%, то покупатель будет согла­сен заплатить сейчас только 92,59 долларов за ценную бумагу, которая через год будет стоить 100 долларов.

100 долларов

Р =------ " о8 — = 92.59 долларов

Чем выше норма процента, тем больше разрыв между текущей стоимостью ценной бумаги и ее стоимостью на момент погашения. При ставке, равной 9% (рассчитанной на основе процентных ставок всех альтернативных инве­стиций этого типа), текущая стоимость будет равна всего 91,74 долларов.

Текущая стоимость ценных бумаг с многолетним сроком погашения

Если ценная бумага представляет собой обязательство уплатить ее владельцу определенную сумму денег через два года после выпуска (допуская отсутствие периодических выплат по процентам), то формула для расчета текущей стоимости такова:

Если процент равен 8%, то покупателе заплатит 85,76 долларов за ценную бумагу, стоимость которой через I года будет равна 100 долларов. Двухгодичная ценная бумага должна быть дешевле одногодичной, чтобы обеспе­чить собственнику эквивалентную норму прибыли.

ЮОдолларов

Р =---------------------------------- --------- = 85.76 долларов

1.1 оо

Формула для расчета текущей стоимости ценной бумаги, удерживаемой в течение п лет, при отсутствии периодических выплат по процентам, выглядит следующим образом:

В отличие от тех ценных бумаг, которые описаны уравнениями 3.4, 3.5, 3.6, по многим ценным бумагам их вла­дельцы получают периодические фиксированные процентные выплаты помимо их стоимости на момент погашения. Цены этих ценных бумаг отражают не только их стоимость на момент погашения, но и величину процентных выплат, Для такой ценной бумаги, имеющей срок погашения, равный п лет, и периодичность процентных выплат один разі год, формула имеет следующий вид:

А А А А М

~ ото+ (Г+о7 + WTW +.................... (ППг+ (Гмг

Где А — ежегодная процентная выплата.

При ставке, равной 8% и сроке погашения 3 года, ежегодной процентной выплате 6 долларов и стоимости на момент погашения, равной 100 долларов, имеем:

6 долларов 6 долларов 6 долларов ЮОдолларов

= П08 + 1.166 + 1.260 + 1.260 =

= 5.56 долларов 5.15 долларов 4.76 долларов 79.37 долларов = 94.84 долларов

В этой формуле чем меньше ежегодные выплаты по процентам, тем ниже предложенная цена облигации. Если бы ежегодная выплата в только что рассмотренном примере была равна S долларам, то предложенная цена была бы равна всего 92,26 долларов. Процент, выплачиваемый чаще, чем раз в год, и предложенная цена, исчисляемая ранее даты купонных платежей, требуют для расчета текущей стоимости ценной бумаги такого типа привлечения более сложных формул.

В этих формулах важнейшими источниками неопределенности является норма процента. Отметим, что платежи по процентам и стоимость на момент погашения облигации в этом случае остаются постоянными. При индивиду­альной покупке облигаций норма процента, определяющая цену ценной бумаги, зависит от процентных ставок аль­тернативных инвестиций в аналогичные облигации. Покупатель ожидает, что получит ту же норму прибыли, какую могут дать другие инвестиции. Ставка процента на рынке отражает ожидаемые ставки процента множества кредиторов и заемщиков.

Ожидаемая норма процента завист от основной реальной нормы процента, которая существует для инвестиций с минимальным риском, от премии за кредитный риск, от ожидаемого уровня инфляции и от срока погашения цен­ной бумаги. Неопределенность проистекает из возможности расхождения между ожидаемым показателем инф­ляции и ее реальным уровнем в будущем. Если в будущем инфляция будет больше, чем ожидалось, то кредиторы проиграют, а заемщики выиграют; если инфляция будет меньше, чем ожидалось, то выиграют кредиторы, а заем­щики проиграют.

Четыре кривые дохода ценных бумаг Государственного Казначейства США

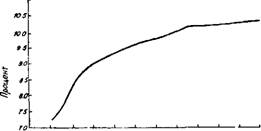
Кривая дохода показывает зависимость между доходом по ценным бумагам определенного типа и сроком по­гашения этой ценной бумаги. Форма этой кривой для каждого вида ценных бумаг изменяется в зависимости от экономических условий. Если ставки процента относительно высоки, и в будущем ожидается их падение, то наклон кривой дохода будет отрицательным. Кривая на 30 июня 1981 года иллюстрирует такую возможность. В периоды относительной экономической стабильности кривая дохода имеет положительный наклон. Кривые 3,4 ил­люстрируют этот случай.

Крибаг'дохода І. ЗОиюнг /98!год

Wt №П ffli tSt* MS tSK Ш/ tSet /Ю fSK Wi

/од погашения

KpuSas догода її, X ребрам >ЭВ2 tod

Гуег /vij ftt* f9rs їж at? /м? /ма /Зїо <эл fS92

Год погашения

Гш тг ач »» от /зз/ тг /юз /т ms <ns Год погашения

Кривые экстраполированы на основании анализа наиболее распространенных выпусков ценных бумаг. Отзываемые выпуски рассматриваются с учетом предварительной даты.

Рис. 3.7

Текущая стоимость акций

Формула цены акций совпадает с формулой 3.7 для облигаций. Цена акции зависит от трех факторов: дивиден­дов, выплачиваемых ежегодно, продажной цены акции и нормы процента для дисконтирования. Выплаты по диви денду занимают место выплат по процентам в уравнении 3.7, а продажная цена акции занимает место стоимости на момент погашения облигации. Однако, неопределенность стоимости акций превышает неопределенность сто­имости облигаций. Для случая с акциями эти три фактора не определены, в то время, как у облигаций не­определенность фигурирует только в норме процента.

При отсутствии изменений в ожидаемых дивидендах и продажных ценах акций, рост ожидаемых процентньи ставок приводит к росту цен акций. В качестве доказательства наличия такой зависимости, рассмотрите рынок цен ных бумаг 1983 года. Здесь цены на акции резко возросли после резкого падения процентных ставок.