Аналитический подход к определению степени точности результатов оценки
 4 ноября, 2011
4 ноября, 2011  admin
admin В основе аналитического подхода к определению степени точности, базирующемся на том, что рассчитываемая с помощью определенной математической модели стоимость объекта является функцией нескольких переменных, а ошибка функции зависит от ошибок переменных и характера модели, лежит точностный анализ этой модели и исходных данных.
Аналитический подход достаточно универсален: ведь точностному анализу можно подвергнуть любую математическую модель оценки, включая оценку и по доходам, и по затратам.
Оцениваемую стоимость У Можно рассматривать как функцию нескольких параметров-аргументов jcb jc2,..., лся, т. е. У -F(X{, хь ...,
Хп), Математическая структура которой может быть довольно разветвленной, так что речь идет о комбинации нескольких элементарных функций, т. е. о функционале. Определение ошибки нелинейных функций осуществляется теми же приемами, что и для линейных функций, но предварительно выполняется линеаризация, т. е. приближенная замена нелинейной функции линейной.
Если функция зависимости стоимости от параметров-аргументов мало отличается от линейной и ошибки параметров-аргументов малы, то используется следующее выражение для определения абсолютной ошибки оцениваемой стоимости:
|
|
Где Ау — абсолютная ошибка оцениваемой стоимости^; Ах,- — Абсолютная ошибка параметра-аргумента *,; П — количество параметров-аргументов в математической модели.
Приведенное уравнение является основным в теории ошибок.
Для оценки стоимости объекта необходимо выполнить ряд математических и логических операций над исходными данными. Совокупность этих операций образует расчетную математическую модель, которую выстраивает оценщик в соответствии с применяемым методом.
Для точностного анализа расчета стоимости необходимо рассмотреть структуру математической модели, на основе которой по правилам из теории ошибок можно построить модель ошибки результатов расчета. Естественно, что эти модели будут различными при использовании разных методов оценки.
Модель расчета стоимости включает несколько элементарных функций, дающих промежуточные результаты. Для каждой из них существует зависимость, по которой можно рассчитать ошибку этой функции исходя из ошибок параметров-аргументов. Эти зависимости выведены на основе известных из теории статистики правил сложения дисперсий (табл. 6.6). Для одних математических функций (сумма, разность, линейная зависимость) удобно вычислять абсолютную погрешность, для других (произведение, частное, степенная зависимость) — относительную погрешность.
Таблица 6.6 Зависимости для определения ошибок элементарных функций
![]()
|
Название функции |
Функция |
Ошибка функции |
|
1. Сумма |
П Ym-T.*t Ы |
|
|
2. Сумма слагаемых с коэффициентами |
Ы |
Ay = Jib? Ax? |
|
3. Линейная функция |
П Y-at-ItbfXt /-I |
Ay^^tbfAx? |
|
4. Разность |
У = х{-х2 |
Ay = Yj Ax:,2 + Axj |
|
5. Разность членов с коэффициентами |
У Vi V2 |
|
|
Ay = J(b]Ax])2+(b2Ax2)2 |
||
|
6. Произведение |
У = П*, I= ИЛИ /=i |
*y=,jhxi |
|
7. Частное |
X Y = — |
By = Y]$x2 + 5^2 |
|
8. Степенная функция |
Y = afxh> I= |
V/=i |
|
9. Показательная функция |
Y = abx |
5y == (In B) xbx |
Примечание: А — абсолютная ошибка, 5 — относительная ошибка.
Как уже отмечалось, ошибки в оценке стоимости во многом предопределены неточностью исходной информации. Поэтому возникает задача выявить значения этих ошибок у показателей, на основе которых проводится оценка.
В работах по теории ошибок для их выявления в исходных данных рекомендуются следующие формальные методы анализа: интервалов варьирования; округленных чисел; таблиц; малой выборки данных.
Анализ интервалов варьирования. Если в информационном источнике указан интервал варьирования показателя, то ошибка определяется довольно просто. Делают предположение о нормальном распределении показателя в границах интервала и примерном равенстве этого интервала «четырем сигмам». В качестве среднего значения берут середину интервала варьирования, а абсолютная погрешность принимается равной половине этого интервала. Такой же подход правомерен и в том случае, когда границы интервала значений показателя определены экспертным путем.
Например, в информационном материале указано, что физический износ машины находится в интервале от 50 до 60%. Это означает, что средняя величина износа равна 55%, а ошибка по правилу «двух сигм» равна (60 — 50)/4 х2 = 5%. Ошибка 5% будет использоваться в дальнейших расчетах ошибки стоимости.
Анализ округленных чисел. Этот метод дает неплохие результаты, если округление показателя увязано с ошибкой его оценки.
|
|
Абсолютная ошибка на уровне «двух сигм» принимается равной ошибке округления, т. е. половине единицы десятичного разряда по последней оставленной значащей цифре в значении показателя. Относительная ошибка рассчитывается по формуле
Где А — последняя значащая цифра приближенного числа; П — количество верных значащих цифр.
Например, в отчете об оценке сообщается, что чистый операционный доход составил 13 560 000 руб. Последняя значащая цифра - 6. Это означает, что относительная ошибка равна (2/6) х ОЛ4"1 = 0,000333, а абсолютная - 13560000 х 0,000333 = = 4516 руб.
Надо иметь в виду, что не всегда фактически взятые значащие знаки в числе являются верными. Обычно указываемое их количество больше, чем верных, поэтому рассматриваемый метод, как правило, занижает ошибки, но в сочетании с другими методами позволяет получить определенную ориентацию в оценке точности исходных данных.
Анализ таблиц. Этот метод применяется тогда, когда исходные данные берутся из таблицы. В таблице значения параметров-аргументов функции разбиты на несколько интервалов и средне -
Му значению параметра в каждом интервале соответствует величина зависимого показателя. Таким образом, при анализе таблицы выявляется погрешность от дискретного представления непрерывной функции, а тем самым косвенно определяется точность отраженного в таблице показателя.
Если функциональная зависимость показателя от параметра-аргумента линейная, то числовые ряды в таблице представляют собой арифметические профессии. Разность между любыми двумя соседними значениями в числовом ряду постоянна и равна разности прогрессии. Абсолютная погрешность показателя Л определяется как половина разности прогрессии Г Числового ряда данного показателя, т. е. А = Г / 2.
Если функциональная зависимость, отображаемая в таблице, является степенной, то числовые ряды представляют собой геометрические профессии. Отношение любого последующего члена ряда к предыдущему постоянно и равно знаменателю профессии ф. В этом случае относительная погрешность 5 определяется по формуле
![]()
Ф + 1
Например, в прайс-листе в виде таблицы указаны цены на круглый прокат из легированной стали в зависимости от диаметра сечения.
Диаметр, мм 8 12 16 20 24
Цена, руб./т 112000 110000 108000 106000 104000
Из таблицы следует, что числовой ряд цен представляет собой арифметическую прогрессию с разностью в 2000 руб., отсюда следует, что абсолютная ошибка на уровне «двух сигм» равна 2000/2= 1000 руб.
Метод анализа малой выборки Может быть приложен к любому промежуточному экономическому показателю, используемому В Процессе расчета оцениваемой стоимости. Порядок применения этого метода был рассмотрен выше в п. 6.2.
Рассмотрим особенности применения аналитического подхода для определения ошибки стоимости при использовании методов сравнительного, затратного и доходного подходов.
Ошибка результата оценки при сравнительном подходе. Точностный анализ результатов при применении сравнительного под -
Хода имеет ту особенность, что он построен на дисперсионном анализе исходных цен на аналоги в сочетании с анализом ошибок функций, по которым рассчитывают корректировки. Порядок дисперсионного анализа цен на аналоги был рассмотрен выше в экспериментальном подходе. Поэтому далее остановимся на учете ошибок, вносимых отдельными корректировками.
Покажем порядок составления моделей оценки и ошибки на примере. Положим, что для оценки стоимости вертикально-сверлильного станка подобрали только один близкий аналог (аналог №1 в табл. 6.5). Сравнение показало, что, во-первых, цена аналога взята на дату, которая на несколько месяцев предшествует дате оценки; во-вторых, станки различаются по главному параметру - наибольшему диаметру сверления; в-третьих, у оцениваемого станка параметр «вылет шпинделя» сокращен по сравнению со стандартным размером.
Согласно описанному выше алгоритму установлена следующая очередность корректировок цены аналога:
• коэффициентная корректировка на момент оценки;
• коэффициентная корректировка на различие по главному параметру;
• поправочная корректировка на нестандартное значение параметра «вылет шпинделя» у оцениваемого станка.
Математическая модель расчета полной стоимости замещения (Sn):
|
|
Где Ц — исходная цена аналога;
/ - корректирующий индекс по фактору времени; К — корректирующий параметрический коэффициент; П — поправка по параметру «вылет шпинделя».
Рассчитанное значение полной стоимости замещения: £п = 35000x1,32 х 1,1 4- 1500 = 52320 руб.
Математическая модель расчета ошибки полной стоимости:
![]()
Где обозначение абсолютной А и относительной 5 ошибки стоит перед тем показателем, к которому эти ошибки относятся.
Для удобства расчетов введем следующее обозначение для скорректированной цены после первых двух корректировок: Цк = = Цх/хК = 35000x1,32x1,1 = 50820 руб.
Получим следующее выражение для ошибки полной стоимости замещения:
![]()
В табл. 6.7 приведен расчет ошибок после корректировок.
Таблица 6.7
Расчет ошибок после корректировок при оценке полной стоимости замещения вертикально-сверлильного станка
|
Корректирующий |
Корректирующий |
Поправка на |
|
|
Показатель |
Временной индекс |
Параметрический |
|
|
/ |
Коэффициент К |
Параметр, П |
|
|
Формула для |
I = h" |
( D Л |
П = />х (Ва- В) |
|
Внесения |
И — средний цеп - |
К= — П |
|
|
Корректи - |
Ной ценовой ин - |
Da) |
Р — «цена» одного |
|
Ровки |
Декс; |
D Da — Наиболь - |
Миллиметра выле - |
|
П — Количество ме - |
Ший диаметр свер - |
Та шпинделя; |
|
|
Сяцев в периоде |
Ления у оценивае - |
В, Ва — вылет |
|
|
Индексации |
Мого станка и ана - |
Шпинделя у оце - |
|
|
Лога; |
Ниваемого станка |
||
|
B — коэффициент |
И аналога |
||
|
Торможения для |
|||
|
Параметра D |
|||
|
Расчет кор - |
/« 1,О358 = 1,3 |
/Г=(ЗО/25)°'52= 1,1 |
П=50х(280-250) = |
|
Ректировки |
= 1500 руб. |
||
|
Исходный |
H |
B |
Р |
|
Показатель, |
|||
|
Вносящий |
|||
|
Ошибку |
|||
|
Размер |
АИ = 0,007 |
Ab = 0,1 |
ЛР=8 |
|
Ошибки ис - |
5А = 0,007/1,035 = |
ЪЬ = 0,1/0,52 = |
|
|
Ходного по - |
- 0,0068 |
= 0,1923 |
|
|
Казателя |
Продолжение
|
Корректирующий |
Корректирующи й |
Поправка на |
|
|
Показатель |
Временной индекс |
Параметрический |
|
|
/ |
Коэффициент К |
Параметр, П |
|
|
Способ оп - |
Наблюдаемое |
Средний интервал |
Проверка колеба - |
|
Ределения |
Среднее отклоне - |
Изменений B Равен |
Ний Рпо Несколь - |
|
Ошибки ис - |
Ние от линии трен - |
0,2 |
Ким моделям стан - |
|
Ходного по - |
Да ± 0,007 |
Ков |
|
|
Казателя |
|||
|
Формула для |
5/= П Х 5/г |
(о) |
АП = (Ва - В)хА/> |
|
Расчета |
InUJ' |
||
|
Ошибки кор - |
|||
|
Ректировки |
|||
|
Расчет |
5/=8x0,0068 = |
5/Г = |
АП = (280 - 250) х |
|
Ошибки кор - |
= 0,0544 |
1п(30/25)х0,52х |
Х 8 = 240 |
|
Ректировки |
Х0,1923 = 0,0182 |
При назначении ошибки исходной цены аналога исходили из 7%-ной варьируемости цен на рынке на одну и ту же модель станка, т. е. 5Ц = 0,07.
После подстановки значений получим:
А5П = >/(50820х0,07)2 +(50820 х0,0541)2 - Ц50820 х0,0182)2 +240 2 = = ^12655094,76+7558991,41 +855484,4 +57600 =4597 руб.;
DSn = 4597/52320 - 0,088.
Таким образом, относительная ошибка оценки полной стоимости замещения равна 8,8%. Приведенное выше выражение для ASn Интересно тем, что оно показывает структуру полученной ошибки и основные факторы ее формирования. Можно видеть, что в данном примере основной вклад в образование ошибки результата дают ошибки, вызванные: 1) колеблемостью цен идентичных товаров на рынке (5Ц) и 2) неустойчивостью ценового тренда (5/г).
Остаточная (с учетом износа) стоимость замещения рассчитывается по формуле So = Sn*( - Ки), где Ки - коэффициент из -
Носа. Так как имеем формулу в виде произведения двух случайных величин Sn И Ки, то относительная ошибка остаточной стои -
|
|
|
Мости: |
Мости: 3S0
|
Где 5КИ — относительная ошибка коэффициента износа. В нашем примере коэффициент износа определяли эксперт-но-аналитическим методом по формуле |
Где 5КИ — относительная ошибка коэффициента износа.
В нашем примере коэффициент износа определяли эксперт-но-аналитическим методом по формуле
Ки Т (0,208 - 0,003хБ) хТ0'7,
Где Б — оценка физического состояния станка в баллах; Т — хронологический возраст оцениваемого станка.
Хронологический возраст станка - величина вполне определенная, поэтому ошибка коэффициента износа связана в основном с неопределенностью оценки физического состояния.
В данном примере хронологический возраст станка равен 8 годам, а физическое состояние характеризуется как «хорошее», чему соответствует среднее количество баллов, равное 40. Подсчитываем коэффициент износа: Ки = (0,208 - 0,003x40) х80'7 = = 0,377 (38%). Состоянию «хорошо» согласно табл. 5.4 соответствует диапазон от 35 до 44 баллов. Подсчитываем значения коэффициента износа в крайних границах этого диапазона, получим изменение Ки от 0,326 до 0,429. Половина интервала равна абсолютной ошибке АКИ = (0,429 - 0,326)/2 *» 0,051. Относительная ошибка равна 5КИ = 0,051/0,377 = 0,135.
Остаточная стоимость замещения So — 52320 х (1 — 0,377) = = 32590 руб.
Рассчитываем относительную ошибку оценки остаточной
Стоимости замещения 5*У0 = >/0,0882 + 0,1352 = 0,161, т. е. примерно
16%.
Абсолютная ошибка остаточной стоимости замещения равна &S0 = 32590x0,161 = 5247 руб.
Поскольку повышение точности всегда сопряжено с дополнительными затратами, то при анализе нужно выявить те исходные данные, которые непосредственно ограничивают точность оценки стоимости. Так, в рассмотренном примере ошибка определения износа вносит большой вклад в конечную ошибку оценки остаточной стоимости объекта, поэтому повышению надежности определения износа следует уделить особое внимание.
Ошибка результата оценки при затратном подходе. Методы затратного подхода моделируют процесс формирования стоимости под влиянием производственно-технологических факторов. Предполагается, что стоимость объекта тем выше, чем больше расход материальных, энергетических, трудовых и других ресурсов на его производство.
|
|
Простым и довольно распространенным примером применения затратного подхода служит определение стоимости объекта исходя из его массы. Масса в этом случае выступает как хорошо осязаемый фактор материалоемкости и технологической сложности производства объекта, что практически реализуется, например, в так называемом «весовом» методе, согласно которому полная стоимость воспроизводства рассчитывается по формуле
Где R — средняя «цена» единицы массы конструкции машины; G — Масса конструкции оцениваемой машины; Кс — коэффициент, учитывающий серийность производства.
Расчетная модель, как видим, имеет форму произведения трех величин, из которых R И Кс можно считать случайными величинами, т. е. носителями ошибки. Принимаем, что масса машины G Задана достаточно надежно.
Относительная ошибка оценки полной стоимости воспроизводства определяется по формуле
|
|
Где 8R — относительная ошибка в определении средней «цены» единицы
Массы; 6КС — относительная ошибка в определении коэффициента серийности.
Обратимся к нашему примеру. Тот же самый вертикально-сверлильный станок необходимо оценить затратным подходом с помощью описанного выше «весового» метода.
Сформируем выборку из 5 моделей вертикально-сверлильных станков, для которых известны цены и масса. В результате статистической обработки информации по методике дисперсионного анализа получим следующие результаты: средняя «цена» единицы массы R - 130 руб./кг, относительная ошибка 5R = 0,083.
Масса станка G = 380 кг. Оцениваемый станок был изготовлен по индивидуальному заказу в условиях мелкосерийного производства, поэтому Кс =1,2.
Полная стоимость воспроизводства станка Sn = 130х380х 1,2 = = 59280 руб.
Ошибку коэффициента серийности Кс находим методом анализа таблицы. Для коэффициента Кс имеем следующий ряд значений.
|
Тип производ - |
Крупно - |
Средне - |
Мелко - |
Единичное |
|
Ства |
Серийное |
Серийное |
Серийное |
|
|
Коэффициент |
||||
|
Серийности |
1 |
И |
1,2 |
1,3 |
Числовой ряд подчиняется арифметической профессии с разностью прогрессии Г = 0,1. Абсолютная ошибка равна половине разности профессии, т. е. АКС = 0,1/2 = 0,05. Относительная ошибка 5КС = 0,05/1,2 = 0,042.
Относительная ошибка оценки полной стоимости воспроиз -
Водства станка равна: 6Sn = Л/°>08з2 + 0>°422 = 0,093.
Коэффициент износа и ошибку коэффициента износа рассчитываем тем же способом, что и при сравнительном подходе. В итоге получаем остаточную стоимость воспроизводства So = 59280х(1 - 0,377) = 36930 руб. Рассчитываем относительную ошибку оценки остаточной стоимости воспроизводства
![]()
Абсолютная ошибка остаточной стоимости воспроизводства равна ASO = 36930x0,164 = 6056 руб.
Ошибка результата оценки при доходном подходе. Методы, базирующиеся на доходном подходе, предполагают прогнозирование будущего чистого операционного дохода (ЧОД) на период эффективного срока бизнеса. Поэтому ошибка оценки стоимости, получаемой этими методами, во многом зависит от того, насколько точно рассчитан ЧОД И прогноз его динамики. ЧОД рассчитывается по разностной математической модели — это разность между выручкой и затратами. С точки зрения анализа точности разностная схема расчета наименее благоприятна, так как разность двух близких чисел обнаруживает значительно большую абсолютную и относительную ошибку, чем ошибки уменьшаемого и вычитаемого в отдельности.
При использовании методов доходного подхода возникает потребность в определении валового дохода от функционирования оцениваемого объекта. Поскольку объектами оценки служат обычно отдельные машины (единицы оборудования), не производящие конечной продукции, а только участвующие в производственном процессе на предприятии, то исчисление валового дохода от их функционирования прямым образом невозможно. Тогда прибегают к косвенным методам. Один из них заключается в использовании показателя фондоотдачи, достигнутого на предприятии, где эксплуатируется оцениваемый объект.
В поставленной задаче этот показатель берется как отношение выручки от реализации (валового дохода) к среднегодовой полной стоимости парка оборудования. Вносится допущение, что показатель фондоотдачи, исчисленный по всему парку оборудования данного предприятия, действителен и для нашего объекта. Тогда условный валовой доход от функционирования оцениваемой машины (единицы оборудования) может быть определен по формуле
|
|
Где Кф0 — показатель фондоотдачи по парку оборудования на предприятии за год, соответствующий условиям наиболее полного использования парка; SM — полная (без учета износа) стоимость оцениваемой машины.
Методом прямой капитализации полная стоимость машины как объекта оценки рассчитывается по формуле
|
|
Где Ем — чистый операционный доход от функционирования машины; Кк — коэффициент капитализации.
ЧОД рассчитывается следующим образом:
Ем = **м — Им,
Где Им — годовые операционные затраты, связанные с функционированием оцениваемой машины (без амортизации).
Если в приведенную выше формулу прямой капитализации подставить значения для Ем и Вм, то
|
|
После преобразований получаем выражение для расчета полной стоимости пользования:
|
|
Модель ошибки при оценке полной стоимости пользования:
|
|
Обратимся к нашему примеру. Нужно определить стоимость пользования для вертикально-сверлильного станка методом прямой капитализации. Ранее мы его оценили сравнительным и затратным подходами.
Операционные затраты Им определяли путем составления годовой сметы расходов на функционирование вертикально-сверлильного станка, т. е. на выполнение технологических операций по сверлению отверстий в деталях (табл. 6.8). Данная смета является бесполуфабрикатной, так как в ней не учитывается стоимость полуфабрикатов (необработанных деталей), поступивших со смежных участков.
Таблица 6.8
Смета затрат на функционирование станка
|
Статья затрат |
Сумма, руб. |
Примечания |
|
1. Инструмент |
1980 |
Годовой расход инструмента в шт. |
|
При цене инструмента за 1 шт. плюс |
||
|
Затраты на его переточку |
||
|
2. Заработная плата ос - |
25100 |
Ставка рабочего-оператора, фонд |
|
Новных рабочих |
Времени с учетом его занятости на |
|
|
Других станках |
||
|
3. Начисления на зара - |
8930 |
35,6% заработной платы |
|
Ботную плату (ЕСН) |
Продолжение
|
Статья затрат |
Сумма, руб. |
Примечания |
|
4. Ремонт и содержа - |
3520 |
По данным завода 880 руб. на одну |
|
Ние оборудования (без |
Единицу ремонтной стоимости (ере), |
|
|
Амортизации) |
Станок имеет 4 ере |
|
|
5. Общепроизводствен - |
25600 |
102% заработной платы основных |
|
Ные и общехозяйствен - |
Рабочих |
|
|
Ные расходы |
||
|
Итого |
65130 |
Коэффициент капитализации рассчитывается согласно теории сложных процентов по формуле шестой функции денежной единицы «Взнос на амортизацию»:
|
|
Где Г - Ставка дисконта;
П — Срок полезного использования объекта оценки в годах.
В рассматриваемом примере принято Г = 15% и П~ 17,5 годам. Срок полезного использования взят как среднее значение для 7-й амортизационной группы (от 15 до 20 лет)1. Результат расчета: Кк = 0,15/(1 - 1,15"17'5) = 0,1642.
Показатель фондоотдачи взят по данным машиностроительного предприятия Кф0 = 1,7.
Полная (без учета износа) стоимость вертикально-сверлильного станка равна:
![]()
Расчет ошибок полной стоимости станка зависит от трех показателей: операционных затрат, показателя фондоотдачи и ко -
!См.: Классификация основных фондов (материальные основные фонды), включаемых в амортизационные группы: Метод, пособие. — М.: Институт оценки природных ресурсов, 2002.
Эффициента капитализации. Расчет этих ошибок выполнен в табл. 6.9.
Таблица 6.9
Расчет ошибок промежуточных показателей
|
Показатель |
Операционные затраты Им |
Показатель фондоотдачи Кфо |
Коэффициент капитализации Кк |
|
Формула для расчета показателя |
5 Где Sj — /-я статья затрат в смете |
Где Вр — выручка от реализации за год; Sno — среднегодовая балансовая стоимость парка оборудования |
|
|
Где Г — ставка дисконта; П — срок полезного использования в годах |
|||
|
Результат расчета показателей |
Им = 65130 руб. (см. табл. 6.8) |
Кф„ =1,7 (поданным предприятия) |
К^ = 0,1642 При Г= 0,15; П = 7,5 |
|
Формула для расчета ошибки |
Где в среднем AS, М 2000 |
Диапазон изменения Г= 0,14.. .0,16; П= 15...20 |
|
|
Колеблемость выручки 10%, колеблемость стоимости парка оборудования 3% |
|||
|
Расчет ошибки |
АИМ = 2000x^5*= = 4472; 5ИМ = 4472/65130 = 0,0687 |
Кк{тп = 0,15099; К^тах = 0,17936; АКЛ = 0,0142; ДК* = 0,086 |
|
|
5Кф0 =Vo,12h-O, O32 = = 0,104; АКфО = 0,104x1,7 = = 0,177 |
Относительная ошибка оценки полной стоимости пользования станка:
|
|
Из приведенной выше формулы видно, что основную долю ошибки стоимости вносит ошибка показателя фондоотдачи, а на втором месте ошибка от неопределенности операционных затрат.
Абсолютная ошибка оценки полной стоимости пользования станка: ASM = 0,1347x42408 = 5714 руб.
Коэффициент износа и ошибку коэффициента износа рассчитываем тем же способом, как и при сравнительном подходе. В итоге получаем остаточную стоимость пользования ^о = = 42408 х (] — 0,377) = 26420 руб. Рассчитываем относительную ошибку оценки остаточной стоимости пользования станка
BS0 = д/о,13472 + О,1352 = О,19 , т. е. примерно 19%.
Абсолютная ошибка остаточной стоимости пользования ASO = 26420x0,19 - 5039 руб.
Аналитический подход к определению ошибки оцениваемой стоимости обладает тем преимуществом, что его можно применить практически к любому случаю оценки, сделав предварительный анализ надежности включаемых в модель исходных данных. Однако недостаток этого подхода состоит в том, что сама схема расчета воспринимается как абсолютно правильная, от чего оцениваемая ошибка результата несколько занижается.

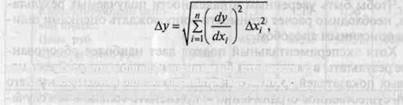
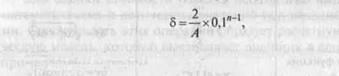
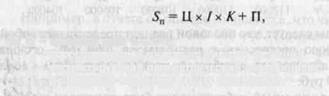
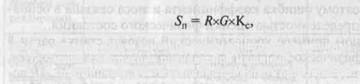
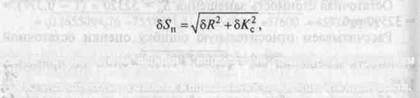
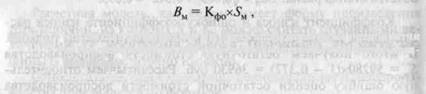
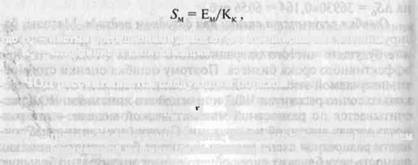
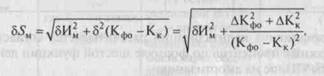
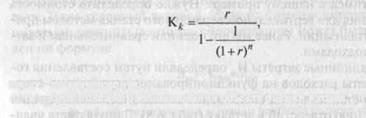

 Опубликовано в
Опубликовано в