В практике оценки довольно часто приходится обращаться к корреляционно-регрессионному анализу для решения разнооб­разных задач: установления связи между стоимостью и потреби­тельскими параметрами объекта; обоснования порядка расчета

Корректирующих коэффициентов при прямом сравнении; выяс­нения трендов цен; установления связи между коэффициентом износа и изменениями влияющих факторов; получения зависи­мостей для расчета себестоимости изготовления объекта и т. п.

В теории математической статистики принято различать два вида анализа: корреляционный и регрессионный.

С помощью корреляционного анализа решается задача уста­новления существенной связи между случайными величинами. Корреляционная связь отражает лишь усредненную тенденцию изменения зависимого стоимостного показателя от изменения одного или нескольких параметров-аргументов. В этом заключа­ется отличие корреляционной связи от функциональной, при ко­торой значение показателя строго определено при заданном зна­чении аргумента (аргументов). Наличие корреляционной связи свидетельствует о том, что зависимость между показателем и ар­гументом (аргументами) подвержена влияниям со стороны дру­гих побочных факторов, одни из которых вообще неизвестны, другие не поддаются оценке и учету.

Обычно речь идет об установлении зависимости стоимости (цены) объекта от технических и эксплуатационных параметров. В случае существенного влияния параметра на стоимость (цену) он признается ценообразующим параметром и принимается к дальнейшему рассмотрению, в противном случае — отбрасывает­ся как второстепенный.

На этапах корреляционного анализа формируется выборка однородных объектов, собирается исходная информация об этих объектах и отбираются основные ценообразующие параметры. Далее подключаются приемы регрессионного анализа, с по­мощью которого выбирается вид регрессионной модели, рассчи­тываются ее параметры и оцениваются параметры ее адекватнос­ти (множественный коэффициент детерминации, среднеквадра-тическая ошибка регрессии и др.). Так как корреляционный и регрессионный виды анализа взаимодополняют друг друга, то мы говорим далее о комплексном корреляционно-регрессионном анализе. Рассмотрим содержание этапов этого анализа.

Формирование выборки однородных объектов. Применение корреляционного анализа предъявляет к исходной информации определенные требования: статистическая выборка объектов должна быть однородной в функциональном и конструктивно-технологическом отношении и достаточно многочисленной. Ис -

Следуемый стоимостный показатель (стоимость, цена, себестои­мость) должен быть приведен к одним условиям его исчисления у всех объектов в выборке. Параметры-аргументы должны быть из­мерены достаточно точно. Требования однородности и полноты выборки находятся в противоречии: чем жестче ведут отбор объ­ектов по их однородности, тем меньше получают выборку, и, на­оборот, для укрупнения выборки приходится включать в нее не очень сходные между собой объекты.

Единство названия или обозначения модели машин еще не означает их полной однородности. Наличие дополнительных уст­ройств придает машине дополнительные функции, которых мо­жет не быть у других машин того же класса. Поэтому требуется проверка на однородность отобранных объектов с точки зрения тождества набора выполняемых функций (операций) у всех объ­ектов, попавших в выборку.

Отбор основных влияющих параметров-аргументов. Если реша­ется задача такого класса, когда надо установить зависимость стоимости (цены) от технических и эксплуатационных парамет­ров объекта, то понятно стремление учесть как можно больше влияющих параметров и построить тем самым более точную мно­жественную регрессионную модель. Однако расширению числа параметров препятствуют два объективных ограничения.

Во-первых, для построения множественной регрессионной модели требуется значительно более объемная выборка объек­тов, чем для построения парной модели. Принято считать, что количество объектов в выборке должно превышать количество параметров-аргументов по крайней мере в 6-7 раз. Отсюда сле­дует, что для построения модели с тремя влияющими пара­метрами надо собрать выборку примерно из 20 объектов с раз­ным набором значений параметров, что практически не всегда удается.

Во-вторых, отбираемые для модели параметры-аргументы должны в своем влиянии на стоимость (цену) быть достаточно независимы друг от друга. Обеспечить это также не просто, пос­кольку выборка обычно объединяет объекты, относящиеся к од­ному семейству или параметрическому ряду машин, у которых имеет место закономерное изменение многих параметров от объ­екта к объекту. Возникающий эффект Мулътиколлинеарности, Т. е. наличия взаимных связей между влияющими параметрами, при­водит к необходимости довольствоваться ограниченным числом

I

Основных параметров. Если этого не учесть, то можно в итоге по­лучить нелогичную регрессионную модель.

Отбор основных влияющих параметров должен опираться как на логический, так и на формальный статистический анализ.

Логический анализ отбора параметров Исходит из понимания того, какую по экономическому смыслу регрессионную модель мы хотим получить. Как известно, стоимость (цена) объекта фор­мируется под влиянием двух определяющих факторов: полезнос­ти объекта и затрат на его создание. Если стремятся получить ма­тематическую модель, отражающую связь стоимости (цены) от полезности, то в качестве параметров-аргументов берут те пара­метры, в которых заинтересован покупатель или пользователь. Именно за эти параметры он готов платить деньги. При таком подходе в итоге получим Ценностную модель, Где в качестве влия­ющих факторов будут выступать факторы функциональных воз­можностей машины: мощность, производительность, качество функционирования.

Другое дело, если стремятся получить математическую мо­дель, которая должна показать зависимость стоимости (цены) от затрат на создание объекта, тогда в качестве параметров-аргумен­тов будут выступать параметры, имеющие в первую очередь зна­чение для изготовителя. При таком подходе получим в итоге Зат­Ратную модель. Примером такой модели служит регрессионная модель, где роль влияющих факторов выполняет масса конструк­ции машины, ее габаритные размеры и занимаемая площадь. Эти свойства действительно сильно влияют на стоимость (цену), от­ражая воздействие производственно-технологических факторов, но не факторов полезности. Ведь разумный покупатель не заин­тересован в приобретении тяжелой и большой машины при про­чих одинаковых параметрах.

В качестве примера рассмотрим технические характеристики однотипных ленточнопильных деревообрабатывающих станков с наклонным столом (табл. 4.3). Эти станки предназначены для прямолинейного и криволинейного распила древесины и древес­ных материалов (рис. 4.4).

Для потенциальных пользователей полезность этих станков отражают следующие параметры: с точки зрения функциональ­ных возможностей — максимальные размеры пропила, размеры рабочего стола; с точки зрения производительности - скорость вращения шкивов и мощность двигателя. Другие параметры (ди -

Таблица 4.3 Технические характеристики и цены ленточнопильных станков

Параметр	Модель станка
SP400	SP500	SP600	SP700	SNA500	SNA600i
1. Диаметр шкива, мм	400	500	600	700	500	600
1 2. Максимальная высота пропила, Мм	250	270	330	380	300	350
3. Максимальная ширина пропила, мм	385	480	580	680	480	580
4. Размеры рабоче­го стола, мм	400x500	500x700	580x810	650x950	500x640	600x830
1 5. Длина пильного полотна, мм	3410/ 3370	3945/ 3860	4580/ 4480	4970/ 4870	4050/ 4130	4520/ 4600
6. Мощность дви­гателя, кВт	0,75	1,8	2,2	2,9	2,0	2,5
17. Скорость вра-| щения шкивов, об/мин	980	900	725	765	800	750
8.Габаритные раз­меры (высотахдли-нахширина), мм	1740х х730х х510	1910х х905х хбЗО	2070х Х1070х Х775	2180х Х1210х Х840	1970х х870х хбОО	2000х ХЮООх Х790
Масса нетто, кг	95	125	240	300	200	280
' Цена на 24.09.04, t евро	1380	2100	2400	2800	2100	2500

Аметр шкива, длина пильного полотна, габаритные размеры, мас­са) дают представление о конструкции, но не несут полезностной нагрузки, поэтому едва ли целесообразно включать их в разраба­тываемую регрессионную модель.

Еще на стадии логического анализа можно также исключить из рассмотрения те параметры, которые тесно связаны с другими параметрами. Для этого определим, например, соотношения между высотой и шириной пропила, длиной и шириной стола у разных моделей (табл. 4.4).

Как видно, пропорции основных линейных размеров у дан­ных моделей станков достаточно стабильны, поэтому из каждой пары указанных параметров можно оставить только один.

Рис. 4.4. Деревообрабатывающий ленточнопильный станок

Таблица 4.4

Показатель	Модель
SP400	SP500	SP600	SP700	SNA500	SNA600
Отношение макси­мальной ширины к максимальной вы­соте пропила	1,54	1,78	1,76	1,79	1,6	1,66
Отношение длины к ширине рабочего стола	1,25	1,40	1,40	1,46	1,28	1,38

В результате логического анализа отбираем следующие пара­метры ленточнопильных станков: максимальная ширина пропи­ла, длина рабочего стола, мощность двигателя и скорость враще­ния шкивов.

Формальный статистический анализ отбора параметров Использует приемы корреляционного анализа. Для этого исследу­ется существенность парных корреляционных связей между стои­мостью (ценой), с одной стороны, и каждым отобранным па­раметром — с другой, а также между самими параметрами. В ка­честве меры тесноты связи между показателями берется парный коэффициент корреляции, который показывает, какая часть об­щей колеблемости одного показателя находится под влиянием другого.

Если один показатель обозначить через У, А другой показатель — через х, то коэффициент линейной парной корреляции между ними рассчитывается по формуле

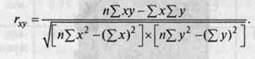
Чем ближе коэффициент парной корреляции по абсолютной величине к 1, тем теснее и определеннее связь между рассматри­ваемыми показателями У И Х. По самой примерной оценке корре­ляционную связь можно считать установленной, если коэффици­ент корреляции по абсолютной величине не менее 0,5.

Расчет парного коэффициента корреляции можно выполнить вручную по приведенной выше формуле, однако современные программные компьютерные средства позволяют решить эту за­дачу довольно быстро и просто.

Программная система MS Excel позволяет автоматически рассчитать коэффициенты парной корреляции с помощью функ­ции КОРРЕЛ. Вначале необходимо подготовить матрицу цены и отобранных показателей, используя следующие обозначения: У — Цена станка, Хх — Максимальная ширина пропила, Х2 — длина ра­бочего стола, х3 — мощность двигателя, х4 — скорость вращения шкивов. Намечаем положение матрицы на рабочем листе MS Excel. Значения элементов матрицы берутся из табл. 4.3 и вво­дятся в соответствующие ячейки рабочего листа. Столбцы полу­ченной матрицы обозначаем Х4, ХЗ, Х2, XI, Y (рис. 4.5а).

Х4	Хз	Х2	Х1	Y
980	0,75	500	385	1380|
900	1.8	700	480	2100
725	2,2	810	580	2400
765	2,9	950	680	2800
800	2	640	480	2100
750	2,5	830	580	2500

	Y	Х1	Х2	ХЗ	Х4
Y	1	0,9697	0,9785	0,9930	-0,8706
Х1		1	0,9890	0,9502	-0,8309
Х2			1	0,9528	-0,8120
ХЗ				1	-0,8755
Х4					1

Б)

Рис. 4.5. Построение матрицы парных коэффициентов корреляции:

А) матрица исходных данных парной корреляции;

Б) матрица коэффициентов

Квадратная матрица коэффициентов парной корреляции (рис. 4.56) заполняется следующим образом. Поочередно выде­ляем ячейки матрицы и находим значения коэффициентов с по­мощью функции КОРРЕЛ.

Например, выделяем ячейку на пересечении строки Y и столбца XI, где должен быть коэффициент корреляции между у их^ На панели инструментов щелкаем кнопку Вставка функции, Открывается диалоговое окно Мастер функций. В Списке Катего­Рия Выделяем Статистические. В окне Функция Находим и выделя­ем КОРРЕЛ, Щелкаем кнопку ОК. Открывается окно КОРРЕЛ. В Поле Массив1 Вводим номера ячеек столбца Y из соседней матри­цы, в поле Массив2 — номера ячеек столбца XI из упомянутой матрицы. Щелкаем ОК И получаем интересующее нас значение парного коэффициента корреляции между у и xh равное 0,9697. Аналогичным образом заполняем остальные ячейки матрицы.

Анализируя матрицу парных коэффициентов корреляции (рис. 4.56), можно обнаружить, что менее всего связан с ценой У Параметр х4, поэтому исключаем его из дальнейшего рассмотре­ния. У оставшихся трех параметров Хь х2 И х3 коэффициенты парной корреляции с У Довольно высоки, но наиболее тесная связь с У Наблюдается у параметров Х2 И Х3. Параметр Х{ Можно исключить из рассмотрения, тем более, что он тесно связан с параметром Х2 (коэффициент парной корреляции между Х{ И Х2 Равен 0,9890).

Для оставшихся параметров Х2 И Х3 Введем новое обозначение: длину рабочего стола обозначим *], мощность двигателя - Х2. Так как каждый из оставшихся параметров тесно связан с ценой Уу То далее построим и исследуем статистические характеристики пар­ных регрессионных моделей У =/(х1) И у —F(X2), А также множе­ственной регрессионной модели У =/(х,, Х2).

Определение параметров регрессионных моделей. Для описа­ния регрессионной зависимости стоимости (цены) от влияющих параметров чаще всего на практике используют линейную или степенную функцию.

В случае парной корреляции, когда выбран один влияющий параметр, связь между стоимостью (ценой) У И влияющим пара­метром Х Отображается с помощью уравнений вида

У — а0 + А{х Или у = UqX01,

У = а0 + А{х Или у = UqX01,

Где я0, А{ — параметры парной регрессионной модели.

В случае многофакторной корреляции, когда рассматривает­ся зависимость стоимости (цены) от нескольких отобранных па­раметров х,, х2,..., Хт, Используют множественные регрессионные уравнения вида

Где j0, tfh Аъ ..., Ат - параметры множественной регрессионной модели.

Степенная функция универсальна, так как аппроксимирует нелинейные связи, каковыми и являются большинство исследуе­мых зависимостей. Она предпочтительна еще и тем, что ее пока­затели степени Ах, аъ ..., Ат Могут быть применены также при оценке объектов методом прямого сравнения при установлении так называемых коэффициентов торможения для отдельных па­раметров.

Параметры регрессионной модели рассчитывают методом наименьших квадратов, суть которого состоит в том, что сумма квадратов отклонений выравненных значений стоимости (цены), т. е. вычисленных по выбранному уравнению связи, от фактичес­ких значений должна быть минимальной.

Средства MS Excel позволяют рассчитать параметры регрес­сионной модели достаточно быстро, кроме того, выводимые так -

Статистические характеристики (коэффициент детермина­ции, критерий Фишера и др.) помогают выбрать наиболее адек-1а гную форму модели и обосновать ее надежность.

Задачу нахождения параметров регрессионной модели пока­жем на вышеприведенном примере с использованием функции ЛИНЕЙН.

Прежде всего проверим достаточность объема выборки для реализации метода наименьших квадратов. Принято считать, что минимальный объем выборки должен превышать количество отобранных влияющих параметров на 3, т. е. Птш = Т + 3. При ко­личестве отобранных влияющих параметров Т = 2 Минимальный объем выборки должен быть равен Птт = 2 + 3 = 5. В нашем при­мере выборка состоит из 6 моделей станков. Следовательно, ус­ловие достаточности данных выполнено.

Функция ЛИНЕЙН позволяет получить параметры и ста­тистические характеристики искомой регрессионной модели

Х2. Намечаем положение матрицы на рабочем листе MS Excel. Значения элементов матрицы берутся из табл. 4.3 и вводятся в со­ответствующие ячейки рабочего листа. Столбцы полученной матрицы обозначаем Х2, XI, Y (рис. 4.6а).

Х2	Х1	Y
1 0,75	500	1380
1,8	700	2100
2,2	810	2400
2,9	950	2800
2	640	2100
2,5	830	2500

I 435,6034	1,074005	538,2627
' 64,53705	0,298344	104,4734 ,
0,997371	32,17756	#Н/Д
568,9747	3	#Н/Д
1178227	3106,185	#Н/Д |

А) б)

Рис. 4.6. Расчет параметров регрессионного уравнения с помощью функции ЛИНЕЙН: А) матрица исходных данных; б) матрица ЛИНЕЙН

Матрицу ЛИНЕЙН, Т. е. параметров регрессионной модели (рис. 4.66), получают следующим образом. Рядом с ранее постро­енной матрицей на рабочем листе выделяем ячейки будущей мат­рицы, у которой количество столбцов равно количеству парамет­ров уравнения (в данном примере 3), а количество строк равно 5.

На панели инструментов щелкаем кнопку Вставка функции, Открывается диалоговое окно Мастер функций. В Списке Катего­Рия Выделяем Статистические. В Окне Функция Находим и выделя­ем ЛИНЕЙН, Щелкаем кнопку ОК. Открывается окно ЛИНЕЙН. В Поле Изв. знач. у Вводим номера ячеек столбца Y из соседней матрицы, в поле Изв. знач. х - номера ячеек столбцов Х2 и XI из той же матрицы, в поле Константа Вводим слово ИСТИНА (если хотим, чтобы в уравнении а0 = 0, то вводим ЛОЖЬ), В поле Стат Вводим ИСТИНА. Затем одновременно нажимаем клавиши Shift+Ctrl+Enter И получаем искомую матрицу.

В первой строке матрицы ЛИНЕЙН Расположены параметры регрессионной модели А2, аь а0. Таким образом, в нашем приме­ре множественная регрессионная модель имеет Вил у — 538,26 + + 1,07.x, +435,6х2.

С помощью функции ЛИНЕЙН Можно построить также рег­рессионную модель степенной формы. Для этого нужно степен -

X2

Ную модель У = A0Xlalx2A2...Xmam Привести к линейному виду, про­изведя ее логарифмирование, в результате чего получим линей­ное уравнение:

В данном уравнении в качестве влияющих параметров высту­пают не сами параметры, а их логарифмы, и зависимой величи­ной служит не цена, а логарифм этой цены.

Обратимся к нашему примеру. На рабочем листе MS Excel предварительно построим матрицу исходных данных: логарифм цены Igy И логарифмы отобранных влияющих параметров Lgx] И Lgx2. Для расчета логарифмов привлекаем функцию LOG. Столб­цы матрицы обозначаем LGX2, LGX1, LGY (рис. 4.7а).

LGX2	LGX1	LGY
-0,12494	2,69897	3,13988
0,25527	2,84510	3,32222 '
0,34242	2,90848	3,38021
0,46240	2,97772	3,44716
0,30103	2,80618	3,32222
0,39794	2,91908	3,39794

0,317829	0,429576	2,020108
| 0,012878	0,027093	0,074201 I
0,999763	0,002123	#н/д
6320,174	3	#н/д
0,05697	1,35Е-05	#н/д

Рис. 4.7. Получение матрицы ЛИНЕЙН для регрессионного уравнения

Степенного вида: а) матрица исходных данных в логарифмической форме;

Б) матрица ЛИНЕЙН

В первой строке матрицы ЛИНЕЙН (рис. 4.76) расположены параметры регрессионной модели А2, аь Lga0. Значение свободно­го члена А0 По его логарифму найдем с помощью функции СТЕ­ПЕНЬ (10;2,020108), получим А0 = 104,7388. Таким образом, в нашем ппимеое множественная оегоессионная модель имеет вид

1 ю влиянию на цену параметры Xj и Х2 Примерно равносиль­ны, что отражают показатели степени у этих параметров в полу­ченной выше множественной регрессионной модели степенного

Вида. Поэтому рассчитаем парные регрессионные модели зави­симости цены от каждого из этих параметров в отдельности.

Парную модель регрессии можно получить двумя способами: либо с помощью функции ЛИНЕЙН, Либо графически.

Начнем с построения парной регрессионной модели линей­ного вида, отражающей зависимость цены У От параметра Х{. На рабочем листе MS Excel предварительно построим матрицу ис­ходных данных, состоящую из столбцов Х{ И У. Столбцы матрицы исходных данных обозначаем XI, Y (рис. 4.8а). Справа от этой матрицы выводим матрицу ЛИНЕЙН Описанным выше спосо­бом (рис. 4.86).

Х1	Y
500	1380 |	2,9927	3,6928
700	2100 |	| 0,3155	237,3880
810	2400 |	0,9574	112,1123
950	2800	(89,9866	4,0000
640	2100	(1131056,6	50276,68
830	2500 |

А)

Б)

Рис. 4.8. Получение параметров парного регрессионного уравнения

Линейного вида: а) матрица исходных данных; б) матрица ЛИНЕЙН;

В) график линии регрессии между У И х,

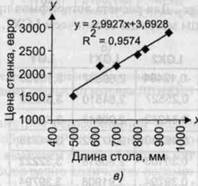
Уравнение регрессии можно получить также путем построе­ния графика средствами MS Excel. Выделяем ячейки данных в столбцах XI и Y. Щелкаем кнопку Мастер диаграмм На панели инструментов. В диалоговом окне Мастер диаграмм (шаг 1) Выби­раем вкладку Стандартные. В Группе Thn Выделяем тип диаграм­мы Точечная. Щелкаем кнопку Далее. Открывается диалоговое окно Мастер диаграмм (шаг 2) С образцом графика (диаграммы). Щелкаем кнопку Далее. Открывается диалоговое окно Мастер диаграмм (шаг 3). На вкладке Заголовки В поле Ось X вводим наз­вание параметра Х1 : Длина стола, мм. В поле Ось Y водим назва­ние У: Цена станка, евро. Щелкаем кнопку Далее. Открывается диалоговое окно Мастер диаграмм (шаг 4), Где указываем место

Размещения диаграммы. Щелкаем кнопку Готово И получаем на рабочем листе график в виде точечной диаграммы. Щелкаем кнопку Формат И указываем Добавить линию тренда. В Диалого­вом окне Линия тренда На вкладке Тип Выбираем тип линии Ли­Нейная, На вкладке Параметры Отмечаем галочкой: Показать урав­Нение на диаграмме И Поместить на диаграмму величину достовер­Ности аппроксимации (RA2). Щелкаем кнопку ОК. На графике по­лучаем линию регрессии, ее уравнение и коэффициент детерми­нации R2 (рис. 4.8в).

Из матрицы ЛИНЕЙН И графика на рис. 4.8 следует, что ис­комая модель регрессии имеет вид У = 3,69 + 2,99Х|.

Последующими расчетами получена степенная модель рег­рессии между у их,: У = 2,08xj1,05.

Аналогичным образом рассчитаны параметры регрессионных моделей между У И Х2. Получены уравнения: линейного вила У = 882,97 + 656,97х2, степенного вида у - 1571,75х20'51.

Выбор итоговой регрессионной модели из нескольких ранее рас­Считанных. Чтобы сделать окончательный выбор из нескольких полученных регрессионных моделей, необходимо проверить каждую из них на тесноту и достоверность связи.

Критерием тесноты связи служит коэффициент детермина­ции (квадрат коэффициента корреляции), который представляет собой отношение регрессионной суммы квадратов к их совокуп­ной сумме:

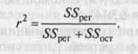
Чем больше ? Приближается к 1, тем выше теснота связи и тем более предпочтительна регрессионная модель при прочих равных условиях.

Так как статистические выводы построены по малой выборке, то высокий коэффициент детерминации еще не гарантирует на­личия действительно сильной связи между переменными. Высо­кий коэффициент детерминации может быть вызван тем, что в малую выборку попали такие случайные объекты, по которым и обнаружилась тесная связь.

Для того чтобы проверить, насколько надежен полученный коэффициент детерминации, применяют тест по критерию Фише­ра. Для этого фактическое значение критерия Фишера /^сравнива -

Ют с его же предельно допустимым значением FnpQR. Если F> Fupejl, То модель считается значимой. Из нескольких сравниваемых моде­лей надежнее будет та, у которой больше разница между Ги Fnpen.

Предельно допустимое значение критерия Фишера является функцией трех параметров: 1) коэффициента а, характеризую­щего приемлемую вероятность ошибки; обычно принимают до­пустимой 5%-ную вероятность ошибки и а = 0,05; 2) количество параметров регрессионной модели К 3) число степеней свободы Df, Которое, как отмечалось ранее, равно разности между количе­ством объектов в выборке П И количеством параметров в модели, т. е. Df=N — K. Общее выражение для предельного критерия Фи­шера: F(A, K, Df).

Предельно допустимое значение критерия Фишера можно получить в системе MS Excel с помощью функции FPACnOBP, Введя показатели D, к, Dfjxnn Рассматриваемой модели.

Определим предельно допустимый критерий Фишера для рассчитанных регрессионных моделей в нашем примере. Оче­видно, этот критерий будет различным у множественных и пар­ных моделей.

Для множественных моделей линейного и степенного вида, показывающих зависимость У =F(Xu Х2), имеем а = 0,05; К = 3; Df = 6 — 3 = 3. С помощью функции FPACnOBP Получаем F(0,05',3;3) = 9,277. Для парных моделей линейного и степенного вида, показывающих зависимости У = / (х) И У = F (х2), Имеем а = 0,05; К = 2; Df= 6 - 2 = 4. С помощью функции FPACTIOBP Получаем F(0,05;2;4) = 6,944.

Значения коэффициента детерминации и фактического кри­терия Фишера для конкретной регрессионной модели можно взять из матрицы ЛИНЕИН.

Теперь проанализируем полученные в нашем примере регрес­сионные модели по коэффициенту детерминации и критерию Фишера. Сопоставление моделей приведено в табл. 4.5. Анализи­руя показатели в этой таблице, приходим к выводу, что наиболее предпочтительной и по показателю детерминации, и по кри­терию Фишера является степенная регрессионная модель У = 104,74х10,43х20,32. Ее и выбираем для дальнейшего использова­ния в операциях по оценке стоимости деревообрабатывающих ленточнопильных станков.

На заключительном этапе корреляционно-регрессионного анализа оценивают вероятную ошибку, которую дает выбранная регрессионная модель.

Таблица 4.5 Сравнительный анализ регрессионных моделей на тесноту и надежность связи

Модель	Коэффициент детерминации	Фактический критерий Фишера	Предельно Допустимый Критерий Фишера
У = 538,26+ 1,07л:, + + 435,6х2	0,99737	568,975	9,277
У Г 104,74jc]M3jc20,32	0,99976	6320,174	9,277
>> = 3,69+ 2,99*,	0,95740	89,986	6,944
>; = 2,08х11'05	0,95158	78,619	6,944
У = 882,97 + 656,97jc2	0,98601	281,967	6,944
У = 1571,75х20'51	0,97988	194,789	6,944

Определение степени точности результата при расчете цены по выбранной регрессионной модели. Мерами точности применяе­мой модели служат среднеквадратическое отклонение, коэффи­циент вариации (достоверности), абсолютная и относительная ошибки.

Среднеквадратическое отклонение показывает степень рассе­яния данных относительно линии регрессии. Для расчета сред-неквадратического отклонения необходимо фактические цены сопоставить с выравненными ценами, т. е. полученными с по­мощью регрессионной модели, используя формулу

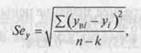
Где^в/ — выравненная цена /-го объекта в выборке, т. е. цена, рассчитанная по регрессионной модели; Yt — фактическая цена /-го объекта в выборке по исходным данным; П — Количество объектов в выборке; К — количество параметров регрессионной модели.

Если выбрана парная регрессионная модель, то среднеквадра­тическое отклонение результирующего показателя У Легко можно получить с помощью функции CTOIIIYX в системе MS Excel.

Расчет суммы квадратов отклонений в нашем примере для выбранной регрессионной модели степенного вида У = 104,74x10,43x20,32 выполнен в табл. 4.6.

Таблица 4.6

Расчет суммы квадратов отклонений

*i	Х2	У	Л	(у*-у)2
500	0,75	1380	1382,57	6,64
700	1,8	2100	2114,42	208,03
810	2,2	2400	2400,69	0,47
950	2,9	2800	2808,67	75,21
640	2	2100	2104,26	18,15
830	2,5	2500	2527,30	745,34
			Сумма	1053,84

Среднеквадратическое отклонение для цены У В нашем при -

Мере при П = Ь и к = 3 Be

= 18,74 евро.

Коэффициент вариации (достоверности регрессии) равен от­ношению среднеквадратического отклонения цены к ее среднему значению:

В нашем примере среднее значение цены (1380 + 2100 + 2400 + + 2800 + 2100 + 2500)/6 = 13280/6 = 2213,33. Коэффициент вари­ации цены (18,74 : 2213,33)х100 = 0,85%.

Абсолютная ошибка в определении цены с помощью регрес­сионной модели рассчитывается как половина доверительного интервала с помощью критерия Стьюдента:

Где T — Критерий Стьюдента при заданной доверительной вероятности Р И

Объеме малой выборки П.

В экономических задачах обычно ограничиваются довери­тельной вероятностью Р= 0,95. В MS Excel критерий Стьюдента можно найти с помощью функции СТЬЮДРАСПОБР. При этом критерий Стьюдента возвращается как функция коэффициента значимости а = 1 — Р И объема выборки, уменьшенного на 1, т. е. П - 1 (числа степеней свободы).

Относительная ошибка определения цены равна отношению абсолютной ошибки к среднему значению цены:

В нашем примере критерий Стьюдента находим с помощью функции СТЬЮДРАСПОБР(а - 0,05; П - 1 = 5), что дает Tpn = 2,57. Абсолютная ошибка расчета цены по регрессионной модели равна (2,57x18,74)/V6~ = 19,66 евро, относительная ошиб­ка равна (19,66 : 2213,33) хЮО - 0,89%.

Рассчитанные по приведенным выше формулам размеры ошибок для цены, определяемой по регрессионной модели, от­носятся к тому случаю, когда влияющие параметры у оценивае­мого объекта находятся в заданных интервалах. Если же парамет­ры выходят за эти интервалы, то ошибка прогрессирует. Напри­мер, рассмотренная выше регрессионная модель для ленточно-пильных станков действительна тогда, когда параметр Х{ (длина рабочего стола) лежит в интервале от 500 до 830 мм, а параметр Х2 (мощность двигателя) — в интервале от 0,75 до 2,9 кВт.