Распределение нагрузок и перемещений по длине соединений при упругом деформировании стыка
 1 февраля, 2013
1 февраля, 2013  admin
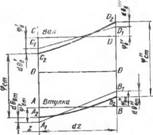
admin Рассмотрим случай передачи соединением крутящего момента. Характер распределения нагрузок и перемещений в посадках может быть установлен [20, 38] путем составления баланса перемещений элемента dz, выделенного двумя поперечными сечениями на расстоянии z от края посадочной поверхности (рис. 4.2). В этом случае угловые перемещения сопрягаемой поверхности определяются: перемещениями втулки и вала от передаваемого крутящего момента; круговыми перемещениями в поперечных сечениях втулки и вала от действующих на поверхности контакта касательных напряжений; перемещениями в стыке сопряженных поверхностей, который рассматривается как третье тело, обладающее особыми механическими свойствами [28]. При упругом деформировании стыка сумма продольных перемещений должна быть равна нулю.
При нагружении соединений крутящими моментами с разных сторон (рис. 4.2, а) в сечение с координатой z втулкой передается момент Mz, а валом — момент М— Mz. При нагрузке с одной стороны в сечение z (рис. 4.2, б) втулкой и валом передается момент Мг. Приращение момента на длине dz составит dMz. Из условия равновесия
DMz = + nddz/2, (4.4)
Где т2 — касательные контактные напряжения в стыке; D — средний диаметр сопряженных поверхностей.
« — с разных сторон; б — с одной стороны от сопряженных поверхностей
Рис. 4.3. Схема закручивания элементов dz втулки и вала
Рассмотрим схему закручивания элемента dz для случая приложения нагрузки с разных сторон сопряженных поверхностей (рис. 4.3). До приложения нагрузки сечения втулки и вала плоскостью, проходящей через ось симметрии элемента dz, совпадают и занимают положение ОО. Под воздействием внешнего крутящего момента сечения ОО втулки и вала изменят свое положение. Если рассматривать только перемещения в стыке, считая его третьим телом [28], то осевые сечения втулки и вала переместятся из положения ОО в положение АВ и С Д. Элементы dz втулки и вала под воздействием передаваемого крутящего момента закручиваются на углы Фвт = Фвт + Фвт и Фв — Фв + Фв и занимают положения Л, В, и CiDi.
На поверхности сопряжения втулки и вала действуют касательные контактные напряжения TZ, которые вызывают круговые деформации в плоскости поперечного сечения. Вследствие неравномерного распределения касательных контактных напряжений по длине поверхности сопряжения элементы dz втулки и вала дополнительно закручиваются на углы d0BT = D&BT - f- d6BT и dQB=dQB + + dQB. Осевые сечения втулки и вала займут при этом положение А2В2 и C2D2. Разность углов закручивания элементов dz втулки и вала компенсируется касательными смещениями в стыке, угловая величина которых ^Фст = Фет — Фет"
Составляя баланс перемещений по замкнутому кон - туру Л2С2ВД, получаем уравнение
Фст + dQВ + фв + Фв + dQB — фст - f dQm — фвт —
TOC o "1-3" h z — фвт + ^бвт —0. (4.5)
Углы закручивания элементов dz втулки и вала
, . г Mzdz..
|
|
Фвт = Фвт + Фвт = г. • (4-6)
^вт* вт
5* 131
, . . (M—Mt)dz
(Рв = Фв + % = ---------- , ,
Где Gвт и GB — модули сдвига материала втулки и вала; 1ВТ, I»—полярные моменты инерции поперечного сечения втулки и вала.
|
(4.7) |
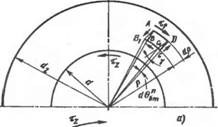
Круговые деформации элементов dz втулки и вала от действующих в стыке касательных напряжений тг определяются выражениями d0BT = DOBT - f d6BT = 61вт — — G2bt; d6B = dQB +dQB = 01B —82B; где 0lBT; 02BT; BIb", 02B — центральные углы поворота точек поверхности контакта в плоскости поперечного сечения втулки и вала на краях элемента dz. Для определения углов 0ВТ и 0В рассмотрим представленные на рис. 4.4 схемы деформаций поперечных сечений втулки и вала под воздействием касательных контактных напряжений TZ. Двумя цилиндрическими и двумя радиальными сечениями выделим элемент ABCD. Под воздействием на боковые грани напряжений тр он займет положение ABXCXD. Угол сдвига (BABi=y, рис. 4.4, а), выделенного элемента Y^tp/G - Из геометрии следует:
Dp Р
(4.8)
(4.9)
|
|
Ю
Где d6gT и — элементарные углы круговой деформации в поперечном сечении втулки и вала. Принимая на основании работ [47, 56] квадратичный закон распределения касательных напряжений по радиусу, получим тр BT=Tzd[2]/4p2; тр „ = тг4р2/(Р. Подставим эти значения в уравнения (4.8), (4.9)
DenBT=J**-JЈ-f (4.10) 4 а„ р»
D6nB = - Ј-pdp. (4.11) <PGB
Интегрируя уравнения (4.10), (4.11) по радиусу, определим углы круговых деформаций
|
D,/ 2 D/2 J 4GBT p* 2GBT I 4 j' Ji <PQB D/2 ' / о |
|
Tz |
D,/2 _ _ D/2 D/2
X РФ:
2GB"
Приращения этих углов на длине элемента Dz
На основе зависимости (4.2) угол сдвига от смещений в стыке <рст=2/СтТ2/^, а его приращение на длине элемента Dz
<*фСт = Фст — Фст — ZKjdxJd. (4.14)
Подставляя формулы (4.4, 4.6, 4.7, 4.12—4.14) в уравнение (4.5), получим после преобразований дифференциальное уравнение второго порядка
Лине соединения с натягом можно оценить с помощью предложенного в работе [43] коэффициента концентрации
G = (4.22)
Тср
2М П<Р1
Пряжения, найденные из условия их равномерного распределения по длине соединения. Подставляя в уравнение (4.22) выражение (4.20), получаем для случая упругого деформирования стыка
% = E-Kz,D _ Ekz/A (4.23)
D М М J
Если GBT/BT>GB/B, то наибольшие касательные контактные напряжения rZmax и соответствующие им g будут в сечении с координатой z=/. При GaT/BT= GB/B Tzmax и g на краях посадки одинаковы. Если GBT/BT< <G„/B, то наибольшая концентрация нагрузки будет при 2 = 0.
В случае приложения крутящего момента с одной стороны от поверхности сопряжения (рис. 4.2, б) все выкладки носят аналогичный характер, но уравнение (4.5) видоизменяется, и его решение М. = М
= - 2ki/d—j— [eHl+z)ld — tHl~z),d]- Касательные напряжения tz и перемещения 6Z в стыке определяются выражениями
X [e*(,+z>/rf - f efc<* z>/rfJ. В этом случае наибольшая концентрация нагрузки будет со стороны ее приложения при любом соотношении жесткостей при кручении втулки и
|
Г) |
|
Где тср = ——^--------- средние касательные контактные на- |
Вала. Коэффициент 6 = №H'd + Ч-
Приведенные соотношения справедливы лишь для случая упругого деформирования стыка при его первоначальном нагружении или после упрочнения.
Аналогично решается задача о распределении нагрузок и перемещений в стыке по длине соединения при передаче осевых усилий. Решение этой задачи для абсолютно жесткой втулки с учетом контактной податливости стыка дано в работе [43], а с учетом податливости стыка и деформации обеих сопрягаемых деталей от касательных и нормальных усилий — в работе [21].

 Опубликовано в
Опубликовано в