Скольжение. Скольжение является причиной износа, уменьшения КПД и непостоянства передаточного отношения во фрикционных передачах. Различают три вида скольжения: буксование, упругое скольжение, геометрическое скольжение.

Буксование наступает при перегрузках, когда не соблюдается условие (11.1): Ft<F. При буксовании ведомый каток останавли­вается, а ведущий скользит по нему, вызывая местный износ или задир поверхности. Нарушение геометрической формы и каче­ства поверхности катков выводит передачу из строя. Поэтому при проектировании следует принимать достаточный запас сцепления К и не допускать использования фрикционной передачи в качестве предохранительного устройства от перегрузки. Применение самоза­тягивающихся нажимных устройств, как правило, устраняет бук­сование.

Упругое скольжение связано с упругими деформациями в зо­не контакта. Элементарно это можно объяснить на примере ци­линдрической передачи (см. рис. 11.1). Если бы катки были абсолютно жесткими, то первоначальный контакт по линии оста­вался бы таким и под нагрузкой. При этом окружные скорости по всей линии контакта равны и скольжения не происходит. При упругих телах первоначальный контакт по линии переходит под нагрузкой в контакт по некоторой площадке. Равенство окружных скоростей соблюдается только в точках, расположенных на одной из линий этой площадки. Во всех других точках образуется сколь­жение.

В действительности явления, которые связаны с упругими де­формациями во фрикционных передачах, сложнее. Они рассмат­риваются в специальной литературе (см., например, [30]). Скольже­ние от этих деформаций не превышает 2...3% и обычно определяет­ся экспериментально.

Для стальных катков упругое скольжение незначительно: £«0,002 (при полной нагрузке); для текстолита по стали £«0,01, резина по стали £«0,03.

С уменьшением нагрузки г уменьшается.

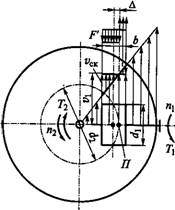
Геометрическое скольжение связано с неравенством скоростей на площадке контакта у ведущего и ведомого катков. Оно является решающим для фрикционных передач. Поиски новых форм тел качения часто связаны со стремлением уменьшить геометрическое скольжение. Природу геометрического скольжения выясним на про­стейшем примере лобового вариатора (рис. 11.8, см. также рис. 11.2). Анализ других случаев см. [30].

Окружная скорость на рабочей поверхности ролика постоянна по всей его ширине и равна Vx. Скорость V2 различных точек диска изменяется пропорционально расстоянию этих точек от центра (на краю диска V2=V2MJ).

При отсутствии буксования скорости V{ и V2 на линии контакта должны быть равны между собой. Однако в рассматриваемой кон­струкции равенство скоростей можно получить только для какой-то одной точки линии контакта. Эту точку П называют полюсом качения. Через полюс качения проходит расчетная окружность дис­ка с диаметром так что

NxN2=D2Dx.

Во всех других точках линий контакта наблюдается скольжение со скоростью V^—Vx— V2. На рис. 11.8 эпюра распределения скоро­стей скольжения по линии контакта изображена жирными линиями. Полюс качения располагается в середине линии контакта только при холостом ходе. При работе с нагрузкой он смещается от

Середины на некоторую величину А. Это смещение можно определить, рассматривая равновесие ролика. Здесь вращающий момент Т{ дол­жен уравновешиваться моментом сил трения. Эпюра сил трения F по­казана на рис. 11.8, где направление сил трения противоположно направ­лению скоростей скольжения, а уде­льная сила трения F

Итак, Т =¥' [(6/2+А) - (Ь/2 - - АМ/2=ВДА/6, (11.15)

Или Д= Txb(DFjf).

Из подобия треугольников опреде­ляем максимальную скорость сколь­жения:

Vd=(2Vl/D2) (У 2+А) = [пщК300] Ф/2 + А), (11.16)

Где щ — в мин"1.

Непостоянство передаточного отношения. Как указано выше, пе­редаточное отношение i&drfdu где d2 зависит от А (рис. 11.8).

Анализируя формулу (11.15), можно отметить следующее:

1. При постоянной силе прижатия Fn величина А изменяется пропорционально нагрузке ^(Г^О и А-*0). При этом передаточ­ное отношение не постоянно. Оно изменяется в некоторых пределах в зависимости от нагрузки.

2. Если нажимной механизм обеспечивает изменение силы при­жатия Fn пропорционально Ти т. е. Ti/Fn=Const, то А и / постоян­ны. В этом большое преимущество саморегулируемых шариковых и винтовых нажимных устройств.

3. Величина А, а следовательно, и изменение г от нагрузки пропорциональны длине линии контакта или ширине ролика Ъ. Для уменьшения скольжения и колебаний передаточного отношения применяют узкие ролики или переходят от линейного контакта к точечному (Ь=0 и А=0). Положение полюса качения связано также с распределением давления по длине линии контакта. При неравномерном распределении полюс смещается в сторону боль­ших давлений. Давление может быть неравномерным вследствие деформаций валов или погрешностей изготовления. С этим связаны высокие требования к точности изготовления и жесткости вари­аторов.

Коэффициент полезного действия. КПД вариаторов зависит в ос­новном от потерь на скольжение и потерь в опорах валов. Потери
на трение скольжения пропорциональны скорости скольжения v^. Формула (11.16) позволяет отметить, что у лобовых вариаторов va уменьшается с увеличением передаточного отношения г. При малых I вариаторы имеют низкий КПД. По этой причине ограни­чиваются диапазоны регулирования некоторых вариаторов. По­тери на трение в опорах зависят от нагрузки на валы, которая определяется в основном силой прижатия Fn (не для всех конструк­ций). При постоянной Fn потери в опорах постоянны и, следователь­но, КПД падает при работе вариатора с неполной нагрузкой. По­этому также целесообразно применять нажимные механизмы с по­стоянным отношением Ti/Fn. Ввиду сложности расчетов величину КПД чаще всего оценивают экспериментально и указывают в спра­вочниках.