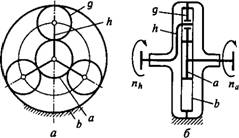
Характеристика и применение. Планетарными называют пере­дачи, содержащие зубчатые колеса с перемещающимися осями (рис. 8.45, а). Передача состоит из центрального колеса а с наружными зубьями, центрального колеса Ъ с внутренними зубьями, водила H и сателлитов G. Сателлиты вращаются вокруг своих осей и вместе с осью вокруг центрального колеса, т. е. совершают движение, подобное движению планет. Отсюда название — планетарные пе­редачи. При неподвижном колесе Ь (рис. 8.45, б) движение может передаваться от а к А или от А к а; при неподвижном водиле H (рис. 8.45, в) — от а к Ъ или от Ъ к а. При всех свободных звеньях одно движение можно раскладывать на два или два соединять в одно, например от Ъ к а и А, от а и H к Ь и т. п. В этом случае передачу называют дифференциальной.

Широкие кинематические возможности планетарной переда­чи являются одним из основных ее достоинств и позволяют исполь­зовать передачу как редуктор с постоянным передаточным отноше­нием; как коробку скоростей, передаточное отношение в которой изменяют путем поочередного торможения различных звеньев; как дифференциальный механизм. Вторым достоинством плане­тарной передачи является компактность, а также малая мас­са. Переход от простых передач к планетарным позволяет во мно­гих случаях снизить массу в 2...4 раза и более. Это объясня­ется следующим: мощность передается по нескольким пото­кам, число которых равно числу сателлитов. При этом нагрузка на зубья в каждом зацеплении уменьшается в несколько раз; внут­реннее зацепление (G и Ь) обладает повышенной нагрузочной спо­собностью, так как у него больше приведенный радиус кривиз­ны в зацеплении [см. знаки «±» в формуле (8.9)]; планетарный принцип позволяет получать большие передаточные отношения (до тысячи и больше) без применения многоступенчатых пере­дач; малая нагрузка на опоры, так как при симметричном рас­положении сателлитов силы в передаче взаимно уравновешиваются. Это снижает потери и упрощает конструкцию опор (кроме опор сателлитов).

193

К недостаткам планетарных передач относятся повышенные тре­бования к точности изготовления и монтажа.

13-2973

Рис. 8.45

Планетарные передачи широко применяют в транспортном ма­шиностроении, станкостроении, приборостроении и т. д.

Кинематика. При исследовании кинематики планетарных пере­дач широко используют метод остановки водила — метод Виллиса. Всей планетарной передаче мысленно сообщается вращение с часто­той вращения водила, но в обратном направлении. При этом води­ло как бы затормаживается, а все другие звенья освобождаются. Получаем так называемый обращенный механизм (рис. 8.4S, *), представляющий собой простую передачу, в которой движение передается от а к Ъ через паразитные колеса G. Частоты вращения зубчатых колес обращенного механизма равны разности прежних частот вращения и частоты вращения водила. В качестве примера проанализируем кинематику передачи, изображенной на рис. 8.45. Условимся приписывать частотам вращения индекс звена (Па, Nh И т. д.), а передаточные отношения сопровождать индексами в на­правлении движения и индексом неподвижного звена. Например, iah означает передаточное отношение от а к А при неподвижном Ъ. Для обращенного механизма

IHAb = (na-nH)l(nb-nh)= -Zb/Za. (8.74)

В планетарных передачах существенное значение имеет знак передаточного отношения. Условимся, что при I>0 вращение ве­дущего и ведомого звеньев происходит в одном направлении; при I < 0 вращение звеньев противоположное. В рассматриваемом при­мере колеса а и Ъ вращаются в разных направлениях, а потому &< 0.

Переходя к реальному механизму, у которого в большинстве случаев практики колесо Ъ заторможено, а — ведущее и H — ведо­мое, на основе формулы (8.74) при пь=0 получаем

Сna-nh)/(-nh)= -zb/za; - najnh+1 = - zb/za

Или

Ibah=na/nh=l+zb/za. * (8.75)

Частоту вращения сателлита определим из равенства

(na-nh)/(ng-nh) = ihag= - zg/za. (8.76)

При заданных па и пн определяют Ng или (Ng—Nh) как частоту вращения сателлита относительно водила или относительно своей оси (используют при расчете подшипников).

Далее,

IBHa=nhlna= 1/4 =zj(za+zb). (8.77)

Для случая, когда неподвижно колесо а, на основе формулы (8.74) при па=О с помощью аналогичных преобразований находим

%h=nbl4=l+zjzb (8.78)

Iahb = nh!nb=zbl(zb+za). (8.79)

Анализ кинематики планетарных передач, выполненных по другим схемам, производят таким же методом.

Ftb и Fth= -2РЦ ?ш—2TaKJ (djiw).)

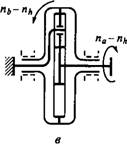
Силы в зацеплении. Из рис. 8.46 ясно, что, по условиям равнове­сия сателлита,

Fta — Ftb

Где Й-1""- 1 ^ (8-80'

Здесь Nw — число сателлитов; Kw — коэффициент, учитывающий неравномерность распределения нагрузки между сателлитами.

Радиальные и осевые силы при известной окружной силе опреде­ляют так же, как и в простых передачах.

Величина Kw зависит от точности изготовления и числа сател­литов.

Структурным анализом* планетарной передачи можно пока­зать, что она является механизмом с избыточными связями. Избы­точных связей нет в передаче с одним сателлитом. Но у такой передачи больше нагрузки на зубья, а следовательно, и габариты. Размещение нескольких дополнительных сателлитов приводит к об­разованию избыточных связей. В механизмах с избыточными связя­ми любые отклонения размеров, например шага зубьев, радиусов расположения осей сателлитов и др., сопровождаются неравномер­ным распределением нагрузки, в данном случае между сателлитами.

'"Структурный анализ механизмов изучают в курсе теории механизмов.

Избыточные связи можно устранить, если выпол­нить одно из центральных колес (чаще колесо а) Самоустанавливающимся, т. е. без радиальных опор. Для этих целей применяют соединение ко­леса с валом по типу зубчатой муфты (см. рис. 17.7). При отсутствии компенсирующих устройств Kw= 1,2...2. В передачах с самоустанавливающим­ся колесом и тремя сателлитами

Kw= 1,1.. .1,2. (8.81)

Для планетарных передач, выполненных по другим схемам, силы в зацеплении определяют по такому же принципу.

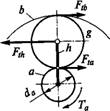
При известных окружных силах нетрудно определить враща­ющие моменты на основных звеньях* передачи, как произведения этих сил на соответствующие радиусы. Для определения моментов и сил в общем виде используют структурную схему планетарной передачи как трехзвенного механизма (рис. 8.47). По условию равновесия,

Та+Ть+Тн=0. (8.82)

По условию сохранения энергии,

7>а+ Tbcob+ Тнсон=0. (8.83)

В этих уравнениях моментам и их произведениям на угловые скоро­сти приписывают знак плюс при совпадении направлений Т я со (ве­дущие звенья) и знак минус, если они противоположны (ведомые звенья). Кроме того, в формуле (8.83) пока не учтены потери на трение.

Два уравнения позволяют определить два неизвестных момен­та при одном заданном и известных со. Например, при ведущем А и закрепленном Ъ (соь=0) с учетом КПД из уравнения (8.83) найдем

Th= - Taribahcoa/coh= - TMh. (8.84)

Из (8.82) имеем

ТЬ=ТМА-1). (8.85)

Потери и КПД. Формула (8.51) остается справедливой для пла­нетарных передач. Потери в подшипниках фи планетарной передачи меньше, чем у простой, так как при симметричном расположении

♦Так называют звенья, которые вращаются вокруг оси водила (основной оси) и воспринимают внешние моменты.

Сателлитов силы в зацеплениях урав-

П

Новешиваются и не нагружают валы т( ___

И опоры. 1-^4 Ь———I

Гидравлические потери фт в плане - " ______________ По/

Тарной передаче при смазке погруже­нием сателлитов в масляную ванну мо - Рис. 8.47 гут быть значительно больше, чем

У простой передачи. Вращающиеся сателлиты входят в масля­ную ванну с ударом и проходят через нее. Поэтому рекоменду­ют неглубокое погружение колес в масляную ванну, а при боль­ших скоростях — применять смазку разбрызгиванием или струй­ную.

Потери на трение в зацеплении ф3 планетарных передач могут быть как меньше, так и больше, чем в простых передачах. Величина Ф3 в значительной степени зависит от схемы и параметров передачи. Это является одной из особенностей планетарных передач. КПД различных типов передач, полученные экспериментально, приведе­ны далее.

Выбор типа планетарной передачи. Существует большое количе­ство различных типов планетарных передач. Их характеристики и анализ можно найти в [27]. Здесь даются только основные указа­ния по выбору типа планетарной передачи. Самое широкое приме­нение на практике получила простейшая передача, схема которой изображена на рис. 8.45. Она с успехом используется как для больших, так и для малых мощностей в машиностроении и прибо­ростроении.

Наиболее рациональные пределы 4=3...9. При этом «0,99...0,97 соответственно.

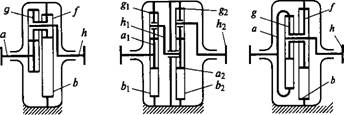
Одна из разновидностей этой передачи с двойным сателлитом изображена на рис. 8.48, а. Передача позволяет увеличить пере­даточное отношение. Здесь

Ft -

Ти

Рекомендуют ft = 7...16 при 0,99...0,96. Передачу требуется изготовлять с повышенной точностью, так как два жестко связан­ных сателлита зацепляются с колесами а и Ь. Эту передачу применя­ют значительно реже первой.

При больших передаточных отношениях в силовых передачах целесообразно применять двух - и даже трехступенчатые простые передачи (рис. 8.48, б). Здесь /=fif2.

На рис. 8.48, в изображена схема передачи с двумя внутренними зацеплениями. В этой передаче при движении от А к а

FjL=l/[l-W(z^)]. (8.87)

А б в Рис. 8.48

При малой разности в знаменателе передача позволяет получать очень большие передаточные отношения (до 1700). Рациональны /=30...100 при ч=0,8...0,65 соответственно. С увеличением I КПД резко снижается и может быть самоторможение. Эту передачу реко­мендуют для кратковременно работающих приводов и маломощных приводов приборов, в которых КПД не имеет решающего значения.

В планетарных передачах находят применение не только цилин­дрические, но и конические и даже червячные колеса. Зубья могут быть прямые или косые, с коррекцией и без нее.

Расчет на прочность. Для расчета прочности зубьев планетарных передач используют те же формулы, что и при расчете простых передач. Расчет выполняют для каждого зацепления; например (см. рис. 8.45), для наружного зацепления — колеса а и G, для внутрен­него — колеса G и Ь. Так как силы и модули в этих зацеплениях одинаковы (см. рис. 8.46), а внутреннее зацепление по своим свойст­вам прочнее наружного, то при одинаковых материалах достаточно рассчитывать только зацепление колес а и G. При разных матери­алах расчет внутреннего зацепления выполняют с целью подбора материала колеса или как проверочный.

При расчете на изгиб используют формулу (8.19).

Для расчета по контактным напряжениям остаются справед­ливыми формулы (8.10) и (8.11) с учетом числа сателлитов Nw и ко­эффициента Kw неравномерности распределения нагрузки между ними. Например, формулу (8.11) при КНа= 1 получим в виде

_______________ /

4 = 1,35 J(8.88) V fodVw Nw И J

Где пщ и Kw — те же, что и в формуле (8.80). В соответствии с условием, принятым при выводе формулы (8.10), при расчете пары А — G по формуле (8.88) полагают, что Dx — диаметр меньшего колеса пары, а и равно отношению числа зубьев большего колеса к числу зубьев меньшего.

Для планетарных передач рекомендуют

(8.89)

0,75.

Выбор чисел зубьев связан с кинематическим расчетом и обычно предшествует расчету на прочность. При заданном I числа зубьев определяют предварительно с помощью формул (8.75), (8.86) и (8.87) в зависимости от типа передачи. Полученные числа уточняют По условиям собираемости планетарной передачи. Рассмотрим эти условия для передачи, показанной на рис. 8.45. Условия соосности

Da/2+dg=db/2 или zg=(zb-za)/2. (8.90)

Условие симметричного размещения сателлитов требует, чтобы Za и zb были кратны числу сателлитов nw.

Условие соседства предусматривает наличие гарантированно­го зазора между сателлитами. С помощью рис. 8.45 нетрудно за­писать

2 (Da/2 + DG/2) Sin (n/nw) > 2 (DG/2+m)

Или

(za+zg) sin (n/nw) > (zg-F 2). (8.91)

Параметры оптимизации планетарной передачи в основном те же, что и у простой зубчатой передачи. Дополнительно рассматривают определение оптимальных чисел зубьев при соблюдении трех усло­вий сборки.

Пример 8.3. Рассчитать передачу по схеме (рис. 8.45) при Ра=22 кВт, па = = 1462 мин"1, 4 = 5,5; нагрузка близка к постоянной, срок службы длительный.

Расчет. 1. Принимаем число сателлитов nw = 3 и определяем числа зубьев. Выбираем za =21 и по формуле (8.75) находим гь=(^-)га=(595—)21 =94,5. При­нимаем zb=93, соблюдая условие симметричного размещения сателлитов. По усло­вию (8.90) zg=(zb-za)l2=(93-21)/2 = 36. По условию (8.91): (21+ 36) sin (я/3)>(36+2), или 49,36 >38, т. е. условие соседства выполняется. При этом действительное пере­даточное отношение 4 = 1 + zb/za = 1 + 93/21 = 5,43 отличается от заданного на (5,5 — 5,43)/5,5' 100% = 1,27%, что меньше допускаемого отклонения — ±4%.

2. Определяем размеры колес пары а — g из условия сопротивления усталости по контактным напряжениям — формула (8.88). Выбираем прямозубое зацепление и назначаем материал колес пары — сталь 40Х (табл. 8.7) при средней твердости
поверхности зубьев колеса а — На=270 НВ (#а=260...280 НВ), а для сателлита g — #£=245 НВ (#£=230...260 НВ).

В конструкции предусматриваем плавающим центральное колесо а и по реко­мендации (8.81) принимаем ATW =1,15. Для рассчитываемой пары колес в формуле (8.88) следует принять: u=zg/za=36/21 =1,71; d{=da и nw= 3. Принимаем также =0,5 [см. рекомендацию (8.89)].

Допускаемые контактные напряжения определяем по формуле (8.55). Предел контактной выносливости для материала сателлита, как менее прочного, согласно табл. 8.8: стт<,=2 НВ +70=2 245+70=560 МПа; 5Я= 1,1. Для длительно работа­ющей передачи NHf>Nhg И Z#= 1 —см. (8.59) и (8.61). При этом =560/1,1 =509,1 МПа. По графику рис. 8.15 (кривая V), Кнр= 1,02, Тх = Та=Ра/соа= =30PJ(n• яа)=30• 22• 103/(я• 1462) = 143,7 Н м=143,7' 103 Н мм. Согласно (8.88), после подстановки данных получаем

, /2,1 • 105 • 143,7 • 103 • 1,02 • 1,15 (1,71 +1) |/;=1,35 3/ - = 70,81 мм;

V 509,12'0,5 3 1,71

Bw=D'apbd= 70,81 0,5 = 35,405 мм. Принимаем bw=35 мм. Модуль зубьев: m=d'Jza= =70,81/21 = 3,372 мм. По табл. 8.1 выбираем т — 3,5 мм из 2-го ряда и уточняем Da=mza=3,5121 =73,5 мм; dg=mzg=3,5 • 36 = 126 мм; db=mzb=3,5 93 = 325,5 мм. Проверяем выполнение условия соседства:

№+4)sin (я/3) >dg+2m,

(73,5 +126) sin 60° > 126 + 2 • 3,5; 172,7 > 133. Условие соседства выполняется.

3. Выполняем проверочный расчет на сопротивление усталости по контактным напряжениям — формула (8.10) при aw=a=20°.

Окружная скорость в зацеплении v=nd(/iJ60=n l3,5' 10"3-1462/60 = 5,62 м/с. По табл. 8.2 назначаем 8-ю степень точности. По табл. 8.3 KhV = 1,24 + 1 38 — 1 24

+--------- —(5,62-5) = 1,27 и, далее, K„=KHpKHv = 1,02* 1,27«1,3.

8 — 5

По формуле (8.10) с учетом Пцг и Kw имеем:

/2,1 • 105' 143,7' 103 • 1,3 • 1,15 /1,71 +1 <гн= 1,18 / =522,5 МПа.

V 73,52 '35 0,6428 3 1,71 /

522,5-509,1

Полученная перегрузка по контактным напряжениям составляет ------------------------ х

509,1

Х -100% =2,6%, что меньше допустимой, равной 5%. Поэтому перерасчета парамет­ров зубчатой пары не требуется (см. п. 6 примера 8.1).

4. Выполняем проверочный расчет на сопротивление усталости по напряжениям изгиба [формула 8.19]. Рассчитываем только зубья сателлита, так как они термооб - работаны на меньшую твердость и подвергаются знакопеременным напряжениям.

По табл. 8.8, fffiim = l>8 НВ= 1,8-245 = 441 МПа. По формуле 8,67, принимая SF= = 1,75; Yn= 1 и Ya=0,7, находим [^ = 441 0,7' 1/1,75 = 176,4 МПа. По графику (рис. 8.20), при х=0 YFS=3,75. По графику рис. 8.15 (кривая V) KFp = 1,02. По табл. 8.3 1 77 — 1 48

KFv = 1,48 + ------- (5,62-5) = 1,54 и, далее, KF= KFp• KFv = 1,02 • 1,54=1,57.

8 — 5

По формуле (8.80) Ft=Fta=2-143,7• 103■ 1,15/(73,5 ■ 3)« 1500 Н.

По формуле (8.19) *F=3,75 '1500* 1,57/(35 3,5)=72,1 МПа<|>^ = 176,4 МПа. Условие прочности соблюдается.

5. Все размеры второй пары «сателлит G — колесо Ь» известны. Поэтому расчет этой пары выполняют в форме проверочного на сопротивление усталости по кон­тактным и изгибным напряжениям. Методика расчета та же, что и для первой пары. Особенности расчета указаны выше.