Краткие сведения о геометрии и кинематике
 31 января, 2013
31 января, 2013  admin
admin Все понятия и термины, относящиеся к геометрии и кинематике зубчатых передач, стандартизованы. Стандарты устанавливают термины, определения и обозначения, а также методы расчета геометрических параметров.
|
|
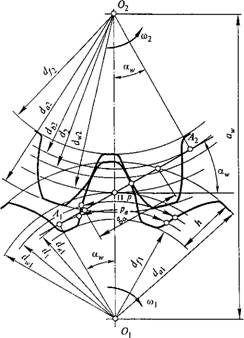
Основные параметры. Меньшее из пары зубчатых колес называют шестерней, а большее — колесом. Термин «зубчатое колесо» является общим. Параметрам шестерни приписывают индекс 7, а параметрам колеса — 2 (рис. 8.4). Кроме того, различают индексы, относящиеся: w — к начальной поверхности или окружности; Ъ — к основной поверхности или окружности; а — к поверхности или окружности вершин и головок зубьев; /— к поверхности или окружности впадин и ножек зубьев. Параметрам, относящимся к делительной поверхности или окружности, дополнительного индекса не приписывают.
Общие понятия о параметрах пары зубчатых колес и их взаимосвязи проще всего пояснить, рассматривая прямозубые колеса. При этом особенности косозубых колес рассматривают дополнительно: гг и Z2 — число зубьев шестерни и колеса; р — делительный окружной шаг зубьев (равный шагу исходной зубчатой рейки); рь=р cosa — основной окружной шаг зубьев; a — угол профиля делительный (равный углу профиля исходного контура), по ГОСТ 13755 — 81, a=20°; a* — угол зацепления или угол профиля начальный:
Cosaw = D cosa/Dw;
|
Примечание. Следует предпочитать 1-й ряд.
|
M=p/n — окружной модуль зубьев (основная характеристика размеров зуба). Модули стандартизованы (ГОСТ 9563 — 80) в диапазоне 0,05... 100 мм (табл. 8.1); D=Pz/N = Mz— делительный диаметр (диаметр окружности, по которой обкатывается инструмент при нарезании); Db = Dcosot — основной диаметр (диаметр окружности, разверткой которой являются эвольвенты зубьев); Dw и dw2 — начальные диаметры (диаметры окружностей, по которым пара зубчатых колес обкатывается в процессе вращения):
Dwi = 2aw/ (Z2/zi +1); Dw2=2Aw - Dwl.
|
Таблица 8.1
|
У передач без смещения и при суммарном сме - щении Xz = 0 (см. ниже) начальные и делительные окружности совпадают:
Dwx = dx=mzx dw2= d2 = mz2.
При нарезании колес со смещением делительная плоскость рейки (делительная окружность инструмента) смещается к центру или от центра заготовки на хт (см. рис. 8.22); х — коэффициент смещения исходного контура. Смещение от центра считают положительным (х>0), а к центру — отрицательным (л:<0).
Aw= 0,5 (dwI+ dw2) — Межосевое расстояние; Aw=M (0,5zL + Xz - Ay),
Где zz = zi+z2; Xz = Xx+X2; Ay— коэффициент уравнительного смещения при XZtЈ0 (определяется по ГОСТ 16532—70, см. также [20]). Для передач без смещения и при хх = —х2 или Xz = 0 Ау=0 Aw = A = Q,5M(Zx + Z2), H = M(2H* + C* — Ay) — высота зуба; Da=D+ + 2M(H* + X — Ау) — диаметр вершин зубьев; я?/= D—2M(А*+ с* — — х) — диаметр впадин; А*—коэффициент высоты головки зуба (по ГОСТ 13755 — 81, А* = 1); с* — коэффициент радиального зазора (по ГОСТ 13755 — 81, с* = 0,25).
Для колес без смещения А = 2,25m; Da=D+2M Df=D—2,5M; АХА2 — линия зацепления (общая касательная к основным окружностям); Ga — длина активной линии зацепления (отсекаемая окружностями вершин зубьев); П — полюс зацепления (точка касания начальных окружностей и одновременно точка пересечения линии центров колес 0Х02 с линией зацепления).
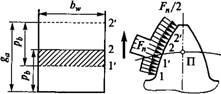
Коэффициент торцового перекрытия ва и изменение нагрузки по профилю зуба. При вращении колес (см. рис. 8.4) линия контакта зубьев перемещается в поле зацепления (рис. 8.5, а), у которого одна сторона равна длине активной линии зацепления Ga, а другая — рабочей ширине зубчатого венца 6W. Пусть линия контакта 1 первой пары зубьев находится в начале поля зацепления, тогда при pb<ga в поле зацепления находится еще и линия контакта 2 второй пары зубьев. При вращении колес линии 1 и 2 перемещаются в направлении, указанном стрелкой. Когда вторая пара придет на границу поля 2', первая пара займет положение Г. При дальнейшем движении на участке Г...2 зацепляется только одна пара зубьев. Однопар - ное зацепление продолжается до тех пор, пока пара 1 не займет положение 2. В этот момент в зацепление вступит следующая пара зубьев и снова начнется двухпарное зацепление.
|
1 |
|
Б |
|
А |
Переходя от поля зацепления к профилю зуба (рис. 8.5, б), можно отметить, что зона однопарного зацепления Г...2 располагается посередине зуба или в районе полюса зацепления (см. также рис. 8.4). В зоне однопарного зацепления зуб передает полную нагрузку Fn, а в зонах двухпарного зацепления (приближенно) — только половину нагрузки. Размер зоны однопарного зацепления зависит от величины коэффициента торцового перекрытия
Ј<Z=GdPb-
По условию непрерывности зацепления и плавности хода передачи должно быть еа>1 [расчет Ба, см. формулу (8.25)].
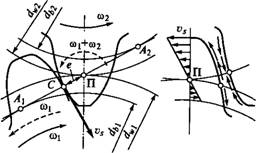
Скольжение и трение в зацеплении. В точках контакта С
|
Рис. 8.6 |
|
Б |
|
А |
(рис. 8.6, а) наблюдается перекатывание и скольжение зубьев. Скорость скольжения Vs как относительную скорость можно определить, используя известное правило механики. Сообщим всей системе угловую скорость coj с обратным знаком. При этом шестерня останавливается, а колесо проворачивается вокруг полюса зацеп
Ления П, как мгновенного центра, с угловой скоростью, равной (ф1 + ш2). Скорость относительного движения (скольжения) в точке С
Vs=e((di + cd2).
Скорость скольжения пропорциональна расстоянию е точки контакта от полюса. В полюсе она равна нулю, а при переходе через полюс меняет знак (направление).
Переходя от линии зацепления к поверхности зубьев (рис. 8.6, б), отметим, что максимальное скольжение наблюдается на ножках и головках зубьев, на начальной окружности оно равно нулю и изменяет направление. Скольжение сопровождается трением. Трение является причиной потерь в зацеплении и износа зубьев. У ведущих зубьев силы трения направления от начальной окружности, а у ведомых — наоборот.
При постоянных диаметрах колес расстояние точек начала и конца зацепления от полюса, а следовательно, и скорость скольжения увеличиваются с увеличением высоты зуба и модуля зацепления. У мелкомодульных колес с большим числом зубьев скольжение меньше, а КПД выше, чем у крупномодульных с малым числом зубьев [см. формулу (8.52)].
Точность изготовления и ее влияние на качество передачи. Качество передачи связано с ошибками изготовления зубчатых колес и деталей (корпусов, подшипников и валов), определяющих их взаимное расположение. Деформация деталей под нагрузкой также влияет на качество передачи. Основными ошибками изготовления зубчатых колес являются ошибка шага и формы профиля зубьев и ошибки в направлении зубьев относительно образующей делительного цилиндра.
Ошибки шага и профиля нарушают кинематическую точность и плавность работы передачи. В передаче сохраняется постоянной только средняя величина передаточного отношения /. Мгновенные
величины I в процессе вращения периодически изменяются. Колебания передаточного отношения особенно нежелательны в кинематических цепях, выполняющих следящие, делительные и измерительные функции (станки, приборы и др.). В силовых быстроходных передачах с ошибками шага и профиля связаны дополнительные динамические нагрузки, удары и шум в зацеплении.
Ошибки в направлении зубьев в сочетании с перекосом валов вызывают неравномерное распределение нагрузки по длине зуба.
Точность изготовления зубчатых передач регламентируется ГОСТ 1643 — 81, который предусматривает 12 степеней точности. Каждая степень точности характеризуется тремя показателями:
1) Нормой кинематической точности, регламентирующей наибольшую погрешность передаточного отношения или полную погрешность угла поворота зубчатого колеса в пределах одного оборота (в зацеплении с эталонным колесом);
2) Нормой плавности работы, регламентирующей многократно повторяющиеся циклические ошибки передаточного отношения или угла поворота в пределах одного оборота;
3) Нормой контакта зубьев, регламентирующей ошибки изготовления зубьев и сборки передачи, влияющие на размеры пятна контакта в зацеплении (распределения нагрузки по длине зубьев).
Степень точности выбирают в зависимости от назначения и условий работы передачи. Наибольшее распространение имеют 6-я, 7-я и 8-я степени точности (табл. 8.2).
Таблица 8.2
|
Окружная скорость, м/с, не более |
|
Степень точности, не ниже |
|
Примечание |
|
ПрямозуБая |
|
Косо - зубая |
(высокоточные)
7
(точные)
8
(средней точности) 9
(пониженной точности)
Высокоскоростные передачи, механизмы точной кинематической связи — делительные, отсчетные и т. п.
Передачи при повышенных скоростях и умеренных нагрузках или при повышенных нагрузках и умеренных скоростях
Передачи общего назначения, не требующие особой точности
Тихоходные передачи с пониженными требованиями к точности
Стандарт допускает комбинацию степеней точности по отдельным нормам. Например, для тихоходных высоконагруженных передач можно принять повышенную норму контакта зубьев по сравнению с другими нормами, а для быстроходных малонагру - женных — повышенную норму плавности и т. п.
Во избежание заклинивания зубьев в зацеплении должен быть боковой зазор. Размер зазора регламентируется видом сопряжения зубчатых колес. Стандартом предусмотрено шесть видов сопряжения: Н — нулевой зазор; Е — малый зазор; С и D — уменьшенный зазор; В — нормальный зазор; А—увеличенный зазор. При сопряжениях Н, Е и С требуется повышенная точность изготовления. Их применяют для реверсируемых передач при высоких требованиях к кинематической точности, а также при наличии крутильных колебаний валов.
Стандарт устанавливает также допуски на межосевые расстояния, перекос валов и некоторые другие параметры.

 Опубликовано в
Опубликовано в