Стержень винта нагружен только внешней растягивающей силой.

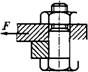
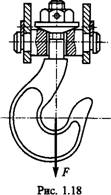
Примером служит резьбовой участок крюка для подвешивания груза (рис. 1.18). Опасным является сечение, ослабленное резьбой. Площадь этого сечения оценивают приближенно по внутреннему диаметру d1 резьбы.

Условие прочности по напряжениям растяжения в стержне

А=^/[(7г/4К2]^[а]. (1.16)

Допускаемые напряжения [о] здесь и далее см. табл. 1.2.

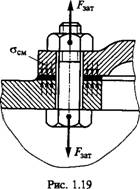
Болт затянут, внешняя нагрузка отсутствует. Примером служат болты для крепления ненагруженных герметичных крышек и люков корпусов машин (рис. 1.19). В этом случае стержень болта рас­тягивается осевой силой F3Ат, возникающей от затяжки болта, и за­кручивается моментом сил трения в резьбе Тр [см. формулу (1.5), где F равна F3„].

Напряжение растяжения от силы F3fLT

C=F2J[(n/4)d12]. Напряжение кручения от момента Тр

Т = Гр/Жр = 0,5/^2 tg (ф + Ф)/(0,2^3). (1.17)

Требуемая сила затяжки

Где А — площадь стыка деталей, приходящаяся на один болт, о^ — напряжение смятия в стыке деталей, величину которого выбирают по условиям герметичности [см. также рекомендации (1.28)]. Прочность болта определяют по эквивалентному напряжению

+ (1.18)

Вычисления показывают, что для стандартных метрических резьб

<7ЭЖ« 1,3(7.

Это позволяет рассчитывать прочность болтов по упрощенной формуле

<Хэж= (1.19)

Расчетами и практикой установлено, что болты с резьбой мень­ше М10...М12 можно разрушить при недостаточно квалифициро­ванной затяжке. Например, болт с резьбой Мб разрушается при силе на ключе, равной 45 Н; болт с резьбой М12 — при силе 180 Н (см. табл. 1.6). Поэтому в среднем и тяжелом машиностроении не рекомендуют применять болты малых диаметров (меньше М8). На некоторых заводах для затяжки болтов используют специальные ключи предельного момента. Эти ключи не позволяют приложить при затяжке момент больше установленного. В таком случае от­падает необходимость ограничивать применение болтов малых диа­метров (при условии, что ключи предельного момента применяют и в эксплуатации).

Болтовое соединение нагружено силами, сдвигающими детали в стыке. Условием надежности соединения является отсутствие сдвига деталей в стыке. Конструкция может быть выполнена в двух вариантах.

F

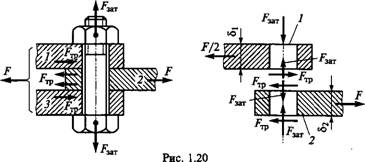
Болт поставлен с зазором (рис. 1.20). При этом внешнюю на­грузку F уравновешивают силами трения в стыке, которые образу-

Ются от затяжки болта. Без затяжки болтов детали могут сдвигать­ся в пределах зазора, что недопустимо. Рассматривая равновесие детали 2, получим условие отсутствия сдвига деталей

= а/,

(1.20)

Или

F3fLT=KF/(if),

Где I — число плоскостей стыка деталей (на рис. 1.20 /= 2; при соединении только двух деталей z==l); /—коэффициент трения в стыке (/«0,15...0,20 для сухих чугунных и стальных поверхностей); К — коэффициент запаса (J5T=1,3...1,5 при статической нагрузке; К= 1,8...2 при переменной нагрузке).

Прочность болта оценивают по эквивалентному напряжению [формула (1.19)].

Отметим, что в соединении, в котором болт поставлен с зазором, внешняя нагрузка не передается на болт. Поэтому болт рассчитыва­ют только на статическую прочность по силе затяжки даже при переменной внешней нагрузке. Влияние переменной нагрузки учиты­вают путем увеличения коэффициента запаса.

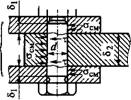
Болт поставлен без зазора (рис. 1.21). В этом случае отверстие калибруют разверткой, а диаметр стержня болта выполняют с до­пуском, обеспечивающим беззазорную посадку. Такая установка болта в отверстие соединяемых деталей обеспечивает восприятие внешней нагрузки стержнем болта. При расчете прочности соедине­ния не учитывают силы трения в стыке, так как затяжка болта в принципе не обязательна[3]. В общем случае болт можно заменить штифтом. Стержень болта рассчитывают по напряжениям среза и смятия. Условие прочности по напряжениям среза

Т=/у[(я/4)<*2*КМ,

Где г — число плоскостей среза (на рис. 1.21, а /= 2; при соединении только двух деталей на рис. 1.21, б /=1).

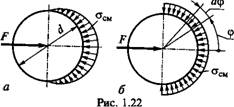
Закон распределения напряжений смятия по цилиндрической поверхности контакта болта и детали (рис. 1.22) трудно установить точно. В значительной степени это зависит от точности размеров и формы деталей соединения. Поэтому расчет на смятие производят по условным напряжениям. Эпюру действительного распределения напряжений (рис. 1.22, а) заменяют условной с равномерным рас­пределением напряжений (рис. 1.22, б). При этом для средней детали (и при соединении только двух деталей)

Ф

(1.22)

F—2 J (Тсм^ОCoscpdcp = (TCM82d,

Или

Для крайней детали

<7см = даЙ1К[<Хсм].

Формулы (1.22) справедливы для болта и деталей. Из двух величин напряжений о^ в этих формулах расчет прочности выпол­няют по наибольшей, а допускаемое напряжение определяют по более слабому материалу болта или детали.

Сравнивая варианты установки болтов с зазором и без зазора (см. рис. 1.20 и 1.21), следует отметить, что первый вариант дешевле второго, так как не требует точных размеров болта и отверстия. Однако условия работы болта, поставленного с зазором, хуже, чем без зазора. Так, например, приняв коэффициент трения в стыке деталей/=0,2, 1,5 и /= 1, из формулы (1.20) получим jfr3aT=7,5JF. Следовательно, расчетная нагрузка болта с зазором в 7,5 раза превышает внешнюю нагрузку. Кроме того, вследствие нестабиль­ности коэффициента трения и трудности контроля затяжки работа

(1.21)

RvfffV

Таких соединений при сдви­гающей нагрузке недоста­точно надежна.

В авиастроении получает распространение постановка болтов с высоким упругоп - ластическим натягом. Таким способом соединяют, напри­мер, листы из дюралевого сплава Д16Т болтами из титанового сплава ВТ-16. Материал бол­тов существенно прочнее материала деталей. При сдвигающих пе­ременных нагрузках наблюдается усталостное разрушение не бол­тов, а деталей в сечении, ослабленном отверстиями под болты. При установке болтов с высоким натягом в зоне отверстия деталей происходят упругопластические деформации. Высокая пластич­ность материала деталей позволяет осуществить натяги до 2% и более от диаметра болта. Это значительно превышает все натяги стандартных посадок.

Долговечность таких соединений в несколько раз превышает долговечность соединений без натяга.

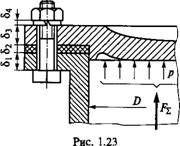
Болт затянут, внешняя нагрузка раскрывает стык деталей. При­мером служат болты для крепления крышек резервуаров, нагружен­ных давлением р жидкости или газа (рис. 1.23). Затяжка болтов должна обеспечить герметичность соединения или нераскрытие стыка под нагрузкой. Задача о распределении нагрузки между эле­ментами такого соединения статически неопределима и решается с учетом деформаций этих элементов. Обозначим: F3AT — сила за­тяжки болта; F=Fz/Z — внешняя нагрузка соединения, приходяща­яся на один болт (Z — число болтов).

После приложения внешней нагрузки к затянутому соединению болт дополнительно растянется на некоторую величину А, а дефор­мация сжатия деталей уменьшится на ту же величину.

Для простоты можно сказать, что только часть внешней нагруз­ки дополнительно нагружает болт, а другая часть идет на разгрузку стыка[4].

Если обозначим х коэффициент внешней нагрузки (учитывает приращение нагрузки болта в долях от силы F), то дополнительная нагрузка болта равна а уменьшение затяжки стыка — (1 — Y)F. Величину коэффициента х определяют по условию равенства дефор­маций болта и деталей, возникающих после приложения внешней нагрузки.

Д = ^ = (1-*)Д*да (1.23)

Где Яб — податливость болта, рав­ная его удлинению при единичной нагрузке; Яд — суммарная подат­ливость соединяемых деталей при том же условии.

Из равенства (1.23) имеем

^Яд/Ое + Яд). (1.24)

Далее получим приращение нагрузки на болт

F* = XF, (1.25)

Расчетную нагрузку болта с учетом (1.19)

F9=lЈF„ + XF (1.26)

И остаточную затяжку стыка от одного болта

(1.27)

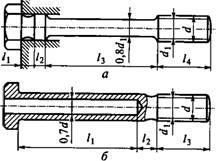
Анализ полученных решений и выбор затяжки соединений. 1. С уве­личением податливости болта Яб и уменьшением податливости де­талей Яд уменьшается х и приращение нагрузки болта F6 [см. фор­мулу (1.25)]. Эту зависимость выгодно используют на практике и особенно при переменной внешней нагрузке F. Например, при изменении внешней нагрузки F от нуля до максимума (рис. 1.24) в расчетной нагрузке Fv болта изменяется только составляющая FQ (по тому же закону, что и F). Как правило, Яд значительно меньше Яб, поэтому F6 значительно меньше F. От переменной составляющей F6 зависит сопротивление болта усталости. Применение упругих болтов (рис. 1.25) является хорошей защитой от усталостного разрушения. Опасным сечением для прочности стержня является сечение по внутреннему диаметру резьбы dx [см. формулу (1.16)]. Учитывая отсутствие концентрации напряжений в ненарезанной части стержня, ее диаметр можно выполнить меньше Dx (рис. 1.25, А) или просверлить здесь отверстие (рис. 1.25, б). При этом болт будет равнопрочным, а его податливость увеличится.

Оптимизация конструкции болта здесь выполняется по условию равнопрочности с целью уменьшения его материалоемкости и по­вышения усталостной прочности.

2. С уменьшением Рж при постоянной F уменьшается F^ [см. формулу (1.27]. При — х)^сила ^ст становится равной нулю,

В стыке появляется зазор. Образование зазора в стыке недопустимо,

И С

Рис. 1.24 Рис. 1.25

Так как при этом нарушается плотность соединения, а при перемен­ной нагрузке появляются удары в стыке, от которых соединение быстро разрушается.

Таким образом, достаточная предварительная затяжка F^ обеспечивающая нераскрытие стыка деталей, является необходи­мым условием надежности и герметичности соединения. Условие нераскрытия стыка: irCT> 0.

Практически нераскрытие стыка зависит не только от величины силы затяжки F3TlT, но и от сохранения ее в эксплуатации. Последнее определяется следующими факторами:

Качеством обработки поверхностей стыка. При большой шеро­ховатости поверхности ее неровности постепенно сминаются, что приводит к ослаблению затяжки. Для ответственных соединений Поверхности стыка деталей рекомендуют шлифовать;

Числом поверхностей стыков. Чем больше поверхностей, тем хуже сохраняется затяжка (на рис. 1.23 число поверхностей стыка равно пяти, считая поверхности под гайкой и головкой болта);

Качеством поверхности и точностью резьбы. Грубая резьба сми­нается и уменьшает силу затяжки. В ответственных соединениях рекомендуют применять гайки, увеличивающие равномерность рас­пределения нагрузки по виткам резьбы (см. рис. 1.16);

Надежностью способа стопорения резьбы (см. рис. 1.9... 1.12); Качеством прокладок. Упругие прокладки в стыке лучше сохраня­ют затяжку. (Отметим, что пружинная шайба (см. рис. 1.23) в этом смысле также выполняет роль упругой прокладки.)

В зависимости от перечисленных факторов, трудно поддающих­ся учету, а также ввиду опасности раскрытия стыка деталей целесо­образно применять высокую затяжку соединений, особенно при переменных нагрузках. Это положение подтверждается практикой эксплуатации резьбовых соединений. На практике рекомендуют принимать

Fзат — K^g^F,

Где А! зат — коэффициент затяжки.

По условию нераскрытия стыка [11, 3]: при постоянной нагрузке Кзят= 1,25...2, при переменной нагрузке АГзат=2,5...4.

По условию герметичности: при мягкой прокладке КзаТ = 1,3...2,5, при метал­лической фасонной прокладке /^ах = 2...3,5, при металлической плоской прокладке А^зат =3—5.

Выбрав Кзлт при известных Лб, Яд или можно определить Fv, F6 и F„ по формулам (1.26), (1.25) и (1.27).

Определение податливости болта и деталей. В простейшем случае при болтах постоянного сечения и однородных деталях (рис. 1.26)

Аб^/бДЯбЛб); АД=<У№А), (1.29)

Где Eq И 2ГД, А^иАц — модули упругости материалов и площади поперечного сечения болта и деталей; IQ — длина болта, участвующая в деформации; да — суммарная толщина деталей; приближенно /g «

(1.30)

В более сложном случае коэффициенты податливости определяют по сумме податливостей отдельных участков болта (см. рис. 1.25) и отдельных деталей (см. рис. 1.23):

I! Еб V*61 Аб2 AqJ*

—+—+»•+—)•

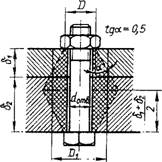
В формуле (1.30) под расчетной площадью АД понимают площадь только той части деталей, которая участвует в деформации от затяжки болта. Условное опреде­ление этой площади в простейшем случае изображено на рис. 1.26. Здесь полагают, что деформации от гайки и головки болта распространяются в глубь деталей по конусам с углом а=30°, или tga«0,5. Приравнивая объем этих конусов к объему цилиндра, находят его диаметр:

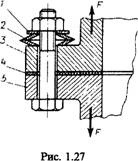
На рис. 1.27 изображено соединение, в котором внешняя нагрузка F увеличива­ет деформацию не только болта, но и деталей 1 и 2 (шайба и набор тарельчатых пружин). Поэтому при расчете коэффициента внешней нагрузки х детали 1 и 2 не­льзя учитывать наравне с деталями 3, 4, 5, деформация которых уменьшается. В таких случаях все детали соединения принято разделять на две системы: детали системы болта, в которых под действием внешней нагрузки абсолютная величина деформаций возрастает (на рис. 1.27 болт и детали 1 и 2); детали системы корпуса, в которых абсолютное значение деформаций уменьшается (на рис. 1.27 детали 3, 4, 5). При этом

(1.28)

5/5 3^1

В соединении на рис. 1.27 набор тарельчатых пружин существенно увеличивает податливость системы болта, а следовательно, уменьшает нагрузку на болт. В об­щем случае задачу о расчете Аа и Ха приходится решать с учетом конкретных, сложных и многообразных деталей (например, литые крышки цилиндров с ребрами, пустотами и т. п.).

Для большинства практических случаев расчет податливости деталей связан с большими трудностями. Между тем расчеты и ис­пытания конструкций показывают, что отношение Яд/(Яб + Яд) неве­лико и не превышает обычно 0,2...0,3. Поэтому для приближенных расчетов соединений без мягких прокладок принимают

Х=Яд/(^ + Яд)<(0,2...0,3). (1.31)

Прочность болта при статических нагрузках. При статических нагрузках прочность болта в соединении типа рис. 1.23 оценивают по формуле

(1.32)

Прочность болта при переменных нагрузках. При переменных нагрузках [см. рис. 1.24 и формулы (1.25) и (1.26)] полное напряже­ние в болте можно разделить на постоянное

<Гт = [^зат + (F6/2)]/A6 И переменное с амплитудой

(7A=(F6/2)A6.

(1.33)

Запас прочности по переменным напряжениям подсчитывают по формуле (см. курс «Сопротивление материалов»)

(1.34)

(ГаКс + фаСТ,

}т

(см. табл. 1.2),

Где сг J—предел вьшосливости материала болта (см. табл. 1.1);

К<, — эффективный коэффициент концентрации напряжений в резь­бе (определяют при испытании затянутой резьбовой пары, а не просто стержня с резьбой); фа&0,1 —коэффициент чувствительно­сти материала болта к асимметрии цикла напряжений.

Величина Ка зависит от многих факторов и трудно поддается учету. Для прибли­женных расчетов рекомендуют [3]: ^«3,5...4,5 — углеродистые стали, — легированные стали. Большие величины относятся к резьбам с D>2Q мм. Указанные величины Ка получены для метрических нарезных резьб и при простых гайках. Для накатанных резьб Ка уменьшают на 20...30%. При применении специальных гаек (см. рис. 1.16), выравнивающих распределение нагрузки по виткам резьбы, Ка уменьшают на 30...40%.

(1.35)

(1.36) (1.37)

Запас статической прочности по текучести материала проверяют по формуле

5Х — бГт/^тах — 0"т/(>т+О (см. табл. 1.2).

Практический (приближенный) расчет затянутых болтов при рас­тягивающей внешней нагрузке. В большинстве случаев величину силы затяжки болтов на практике не контролируют, поэтому смысл точного расчета теряется. Для приближенного расчета, учитывая рекомендации (1.31), принимают / = 0,2...0,3. При этом

Fv= l,3f3aT + (0,2...0,3).F.

Величину выбирают по рекомендациям (1.28). Далее в зави­симости от Характера нагрузки используют формулы (1.32) или (1.34) и (1.35).

Прочность болтов при высоких температурах. При высоких тем­пературах в болтовом соединении могут возникать дополнительные температурные нагрузки. Эти нагрузки возникают в том случае, когда температурные коэффициенты линейного расширения мате­риалов болта и соединяемых деталей не одинаковы. Температурные нагрузки подсчитывают по условию совместности деформаций, ко­торые рассматривают в курсе «Сопротивление материалов». Тем­пературные напряжения в болтах понижают путем применения материалов с близкими температурными коэффициентами линей­ного расширения или постановки упругих прокладок, упругих бол­тов и шайб.

При температурах свыше 150 °С для легких сплавов и 300 °С для конструкционных сталей в затянутых соединениях становятся су­
щественными явления релаксации и заедания. Релаксация связа­на с ползучестью материала при высоких температурах. Она проявляется в постепенном ослаблении затяжки соединения. При этом нарушается одно из главных условий прочности и герметич­ности соединения. Для уменьшения релаксации необходимо повы­шать упругую податливость деталей соединения, применять мате­риалы с высоким пределом ползучести (например, хромистые и хромоникелевые стали [3]), снижать допускаемые напряжения для болтов.

После некоторого времени работы при высоких температурах наблюдается заедание в резьбе, которое проявляется в том, что гайку не удается отвинтить или она отвинчивается с большим трудом, а резьба портится или разрушается. Для борьбы с заедани­ем необходимо изготовлять гайки из материалов, обладающих более высоким температурным коэффициентом линейного расшире­ния по сравнению с материалом винта (перлитный чугун, бронза, латунь, жаропрочные стали); применять покрытия — омеднение или хромирование резьбы; применять более крупные резьбы с зазо­ром по среднему диаметру.