ТРЕЩИНОСТОЙКОСТЬ БЕТОНА
 20 января, 2013
20 января, 2013  admin
admin Бетон является сложным гетерогенным материалом, поведение которого под нагрузкой можно рассматривать как поведение двухкомпонентной системы: на макроуровне— «заполнитель — раствор» и мезоуровне — «заполнитель — цементный камень».
Вследствие различия в физико-механических свойствах составляющих бетона в процессе твердения, цементного геля возникает внутреннее поле напряжений, распределение которых не подчиняется законам сплошных сред. Значительное влияние на неоднородность поля напряжений оказывают форма, рельеф и чистота поверхности зерен заполнителя, гранулометрический состав и содержание его в бетоне. В связи с этим прочность сцепления заполнителя с цементным камнем существенно влияет на прочность бетона; она составляет 50—65% предела его прочности при растяжении, зависит от рельефа поверхности зерен заполнителя и содержания воды в цементном геле.
При исследовании структуры цементного камня как сплошной среды, в которую вкраплены шарообразные тела различной плотности (от гранита до воздуха), определено [58], что вблизи малых неоднородностей, расположенных на границе с большими неоднородностями, локальные напряжения могут превосходить в 9 раз сжимающие. При низком пределе прочности материала он может разрушиться одновременно от разрыва в направлении приложения внешней нагрузки и раздробления перемычек между порами (пустотами) в направлении, перпендикулярном к действию нагрузки. Поэтому материал с порами разного размера менее прочен, чем с порами одного размера.
Как следует из исследований на модели (см. рис. 11.1), процесс микроразрушений цементного камня проходит через две стадии, выражающиеся уплотнением и разуплотнением его микроструктуры. Аналогичным образом происходит деструкция мелкозернистого (песчаного) бетона, являющегося относительно более однородным материалом, чем бетон с крупным заполнителем.
Крупный заполнитель кардинально изменяет кинетику микроразрушений бетона. Если мысленно внести в модель, изображенную на рис. 11.1, включения, имитирующие зерна крупного заполнителя, тогда между ними и двухслойными дисками следует поместить силы связи сцепления С3, меньшие по величине, чем С и С2. При таком дополнении модели под влиянием внешней сжимающей нагрузки процесс микротре- щинообразования бетона будет характеризоваться четырьмя стадиями.
На первой стадии (при начальном нагружении) произойдет уплотнение кристаллогидратной структуры цементного камня и по мере роста уровня обжатия возникнут градиенты напряжения в контактных связях С3, которые приведут к их разрыву, т. е. к образованию микроразрушений в этих зонах и нарушению сцепления между ними (вторая стадия). Включения, лишенные связей сцепления, с дальнейшим увеличением внешней нагрузки будут сминать прослойки цементного камня (разделяющие включения), т. е. произойдет кажущееся его уплотнение за счет разрушения стенок пор (третья стадия). Эта стадия деструкции является подготовительной, способствующей наступлению прогрессирующего процесса разуплотнения всей системы (четвертая стадия), ведущего к разрушению структуры цементного камня и отделению от него в первую очередь более крупных включений.
Поведение модели при сжатии согласуется с результатами исследований кинетики разрушения бетона [33, 44, 71, 114] и подтверждает правильность высказанного положения о том, что стадиям разрушения бетона всегда предшествует стадия уплотнения. Это положение устраняет известные противоречия, при которых считают, что процесс разуплотнения бетона должен происходить в период продолжающегося уменьшения его объема при сжатии.
При исследовании шлифов бетона обнаружено [164], что даже перед его разрушением в крупном высокопрочном заполнителе трещин мало и они не влияют на прочность конгломератного материала. Зерна заполнителя обычно разрушаются после образования сети трещин в цементном камне. Трещины сцепления возникают еще в процессе усадки цементного камня, т. е. до нагружения бетона преимущественно в контактах с крупными зерна
ми заполнителя, на поверхности которых наблюдается большое скопление пузырьков воздуха. Под нагрузкой трещины сцепления прогрессируют, одновременно они появляются в прослойках цементного камня между зернами заполнителя, и при их объединении в общую систему с определенной ориентацией по отношению к приложенной нагрузке бетон разрушается.
Влияние зерен крупного заполнителя на кинетику микроразрушений бетона может сказаться различно, так как это зависит от соотношения прочностей и модулей упругости цементного камня RK, Ек и заполнителя RK3, Екз. При достаточно высоких значениях /?к, RK^RK и ЕКЗ>ЕК разрушение бетона может происходить как от раскалывания заполнителя и разрыва цементного камня, так и вследствие нарушения сцепления между ними (бетон на плотном заполнителе). Если же RK^>RK3 и Ек> >ЕКЗ, то разрушение произойдет в результате раздробления зерен заполнителя и раскалывания цементного камня (легкие бетоны на пористом заполнителе). Эти деструктивные процессы могут проявляться раздельно в определенной последовательности или одновременно в зависимости от деформативных и механических свойств составляющих.
|
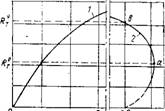
Рис. 11.3. Диаграммы сжатия с— е (/) и изменение объема бетона при микротрещинообразовании (2) |
Уровень напряжения соответствующий началу образования микротрещин, характеризует предельное состояние структуры бетона при определенных деформативных и прочностных свойствах [32]. Из рис. 11.3 следует, что Rr соответствует максимальному уменьшению объема образца бетона, обусловленного сжатием кристаллогидратных образований. С увеличением нагрузки деструкция материала прогрессирует и при восстановлении его объема до первоначальной величины (AQ=0) процесс возникновения микротрещин достигает глобального развития при некотором уровне напряжения R характеризующем верхнюю условную границу микротре-
щинообразования (по существу, предел прочности бетона) .
Связующим звеном между пределом упругости и началом процесса образования трещин может служить
Структурный коэффициент бетона K=f (Is, ~ ), ко-
Ек Уб /
Торый предопределяет влияние как бы наследственных факторов на предельные напряжения при трещинообра - зовании. С увеличением относительного количества крупного заполнителя УКз (в долях единицы) значение /?т° снижается вследствие больших деформаций, возникающих в прослойках цементного камня, поэтому i?? зависит от состава бетона.
Отношение RTIRTw Для образцов раствора выше, чем для бетона на том же растворе, и в этом случае RT/RHР бетона может отражать влияние параметров /Гкз/^рс и Укз/Уб на уровень напряжения, при котором начинается микротрещинообразование. В связи с изложенным суммарный коэффициент концентрации напряжения /Сс= (Кр+/С), где Кр — коэффициент концентрации от
D
Усадки, может быть определен как отношение др0рас,
|
ТАБЛИЦА 11.2. ЗАВИСИМОСТЬ Кс ОТ ХАРАКТЕРИСТИК СОСТАВА БЕТОНА [103]
|
Из табл. 11.2 видно, что с уменьшением RR — коэффициента раздвижки щебня (отношение объема раствора к объему пустот в щебне), значения Кс возрастают, a RVRUv снижаются, т. е. увеличение содержания щебня ускоряет начало образования трещин.
|
|
|
Б) К* |
Для оценки внутреннего поля напряжения структуры бетона при сжатии может быть использована его аналоговая модель, состоящая из матрицы — растворной части и равномерно распределенных по всему ее объему вклю - /257 Рис. 11.4. Распределение напряжений
А — на позерхности раздела «матрица — включение»; б — зависимость KА
От -----------
-РС
|
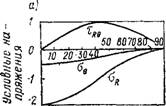
Рис. 11.5. Зависимость Ka и Kx А — от углового радиуса г; б — от геометрии включений: /, 2, 3 и 4 — |
|
Fs2 /,8 А/3 |
Чений сферической формы, одинакового диаметра, имитирующих зерна крупного наполнителя. На основании такой модели показано [23], что если модуль упругости включения Екз=оо, то при одноосном сжатии на сферической границе раздела «матрица — включение»: нормальные ад, тангенциальные ае и касательные тд0 на - пряжения могут быть при р, п=0,2 выражены уравнениями:
= 6ср О + Cos 2е>; бе = °>258ср (1 + cos 2е);
^e = Scpsin2e, (11.9)
Где сгСР — среднее сжимающее напряжение; 9 — сферическая координата.
Значения радиальных напряжений для большого диапазона соотношений ЕКз/ЕрС при условии, что ЕКз^Ерс и IXп = 0,2, можно определить зависимостью
Екз
РЕр9 (1 + cos28). (11.10)
"f52" +1
Согласно формуле (11.10), коэффициент концентрации нормальных напряжений 7(с=(ГктахМр приближа-
Ется к 2 по мере роста —— от 1 до оо (рис. 11.4, б). При
£рс
Этом наиболее существенное увеличение Ка достигается при условии
^рс
Изменение формы включения от сферической к кубической способствует неограниченному увеличению Да. График KQИ концентрации касательных напряжений
Кх = toemax/ffcp (рис. 11.5, а) свидетельствуют о резком увеличении К0 при значении углового радиуса г^0,2В (где В — длина ребра куба) и зависимости Кт от г на всем интервале уменьшения г/В. Крупность включений также влияет на концентрацию напряжений. Увеличение высоты ребра Л прямоугольного параллелепипеда (рис. 11.5,6) вызывает линейный рост Ко, если ЕКз/Ерс = оо. При Екз/Ерс=4 значение Ко медленно возрастает с увеличением Л/В, а затем при Л/В >1,4, остается постоянным. Аналогично изменяется Ко, если Ек. з/Ерс = 8; в этом случае характерная точка, после которой /Саимеет постоянные значения, соответствует Л/В~ 1,6. Если упругие свойства составляющих идентичны, то задача упрощается, так как мы уже имеем дело с однородным изотропным твердым телом, к которому приложена равномерно распределенная сжимающая нагрузка: здесь KG= 1 независимо от Л/В.
Слабым звеном в системе «матрица — включение» является поверхность их раздела, где образуются микротрещины, нарушающие сцепление двух составляющих. Микротрещинообразование обусловлено наличием растягивающих напряжений в экваториальной полости включений, близких по значениям к пределу прочности при растяжении растворной части (матрицы). Если эти напряжения принять за критерий начала микроразрушений бетона, нормальное напряжение растяжения aRp можно выразить зависимостью:
АЛр==-0,186асракз. (11.11)
Коэффициент аКЗ учитывает взаимодействие заполнителей и растворной части при различных относительных объемных содержаниях и модульных соотношениях составляющих бетона. При соблюдении граничных условий
^ 1 аКз> тхг (где К= ; GK3 и Gpc — модули
Е рс A-f-1 Сгрс
Сдвига заполнителя и растворной части) и УКз=0, коэффициент аК.з может быть выражен в виде
«КЗ = __________ -РС (11.12)
Екз
Р (1 + 2VK3)
После подстановки (11.12) в выражение (11.11) получим:
% =-М22аср-------------- Рс-------------
Ьрс
Заменив аДрна RP— предел прочности бетона при растяжении, а (Тер на будем иметь:
R°T =—2,81? ------ f-------------- . (11.13)
Ькз у
С икз Ьрс
Как следует из табл. 11.3, с увеличением содержания крупного заполнителя Rp сначала возрастает до некоторого предела, соответствующего оптимальному насыщению бетона заполнителем, а затем снижается. Формула (11.13) не учитывает в явном виде влияние формы заполнителя; эту функцию выполняет RPl хотя для реаль-
|
ТАБЛИЦА 11.S. ЭКСПЕРИМЕНТАЛЬНЫЕ И РАСЧЕТНЫЕ ЗНАЧЕНИЯ Д°В ЗАВИСИМОСТИ ОТ ОПРЕДЕЛЯЮЩИХ ПАРАМЕТРОВ
|
Ных соотношений составляющих бетона-влияние формы невелико.
Предел прочности бетона оптимальных составов при растяжении может быть определен по известной эмпирической зависимости: ___
= СР V&cx * (И-14)
Для бетона марок 300 и более Ср=0,375, а при более высоких марках Ср=0,278.
Удовлетворительное согласование расчетных значений с экспериментальными данными (см. табл. 11.3) свидетельствует о применимости формулы (11.13) для определения R° еще на стадии расчета состава бетона путем подбора его составляющих по их механическим и деформативным свойствам.
Формулу (11.13) можно использовать при определении R? для легкого и песчаного бетонов. В последнем случае вместо Vm и в формулу (11.13) должны
£рс
£
Быть подставлены значения —— ; Умз — содержание в
Растворе песка и R$K — прочность цементного камня при растяжении. Исследования прочности и деформаций аглопоритобетона на кварцевом песке показали, что с уменьшением ВЩ цементного геля в 1,45 раза R° возросла в 1,22 раза. Повторное вибрирование через 30 мин после первичного уплотнения бетонной смеси повысило
R° на 24%, а увеличение расхода цемента с 306 до 580 кг/м3 способствовало росту R° на 60% при практически неизменном отношении R°JRnР. При прочих равных условиях аглопоритобетон характеризуется более высокими значениями R°, чем бетон на плотном щебне вследствие более высокой прочности цементного камня в первом случае.

 Опубликовано в
Опубликовано в