РАЗРУШЕНИИ ПЛЕНОК
 3 декабря, 2012
3 декабря, 2012  admin
admin Пленка пены при достижении определенной (критической) толщины разрушается. Это третий важный фактор разрушения пен в процессе их старения. Механизм разрушения юлслых и тонких черных пленок не одинаков. Это обусловлено тем, что благодаря наличию прослойки раствора между адсорбционными слоями обе поверхности толстой плепкн могут рассматриваться независимо.
Согласно теории разрыва толстых пленок Де Фриза [141] разрушение происходит вследствие образования отверстия критического размера. Возникновение этого отверстия (имеет флук - туациониое происхождение) сопровождается уменьшением поверхностной эпергпн, поскольку, по крайней мере в начальный момент, поверхность раздела при разрыве пленки увеличивается (рис. 36).
|
(4.56) |
|
Где Гмин — минимальный радиус отверстия Максимальное увеличение поверхности раздела А5макс достигается [122] при
|
|
(1.57) 83 |
Прирост общей поверхности разрушающейся плепкн толщиной б можно вычислить по уравнению [141]
AS = л-6 (гыни + 6/2 - 6/л) - 2л (гшм1 + 6/2)-
Максимальное увеличение поверхностной энергии при расширении отверстия (энергия активации) составляет:
Аймаке = аД5 = 0,736% (4.58)
Из уравнения (4.58) следует, что процесс разрушения в большей степени зависит от толщины пленки, чем от поверхностного натяжения. Поэтому вероятность разрыва больше для пленок меньшей толщины. Энергия активации при 6 = 15 нм и о=30—40-10~3 Н/м составляет «5-10 18 Дж. Пленки из чистой жидкости могут иметь значительно меньшую толщину, соизмеримую с размером молекул жидкости, поэтому самопроизвольное разрушение такой пленки невозможно предотвратить.
Энергия активации, указанная выше, довольно велика, и поэтому пленки толщиной более 15 нм практически не должны разрываться, хотя это противоречит имеющемуся опыту. По - видимому, описанный механизм разрыва неправомочен.
В соответствии с представлениями А. Шелудко разрыв пленки обусловлен образованием на поверхностях пленки искривленных участков. Они возникают под действием тепловых флук - туаций и приводят к локальным изменениям толщины пленки. На утолщенный участок пленки действуют возникающие в нем местное капиллярное давление АРк и отрицательное расклинивающее давление П с направлением, противоположным капиллярному, которое восстанавливает толщину пленки. Если нарастающее расклинивающее давление по абсолютной величине превышает капиллярное давление, локальный прогиб плепкн увеличивается, и она разрушается. Из условия разрыва пленки dU/d6 = dApddb получено уравнение для се критической толщины:
М-т^Г
Эю уравнение справедливо при допущениях: Дб-Oi (Дб — прогиб пленки; К — длина волны прогиба); R=K2/32д6 (R — радиус сферы волны на поверхности); П=—А/бяб3 (А — константа Гамакера).
Уравнение (4.59), полученное также в работе [163], не учитывает влияния электростатической составляющей расклинивающего давления, поэтому оно справедливо только для нестабильных пленок. Кроме того, оно содержит величину К, данные о которой еще отсутствуют. Однако имеются основания полагать, что длина волны прогиба поверхности пленки пропорциональна ее радиусу. Образование волн на поверхности пленки вследствие теплового движения наблюдали при изучении рассеяния света пленками [163]. Различают две составляющие флуктуаций, вызывающих разрушение пленок: быстрые и медленные [164]. В присутствии ПАВ быстрые флуктуации вытесняются медленными и поверхность пленки как бы «замораживается».
Согласно теории А. Шелудко для разрыва пленки не обязательно достижение критической толщины 6Кр - Если существует устойчивая толщина 6<6Кр, то в пленке должны образовываться тонкие места в виде «черных пятен» с толщиной 6. В достаточно толстой пленке истечение жидкости происходит обычно быстрее, чем в тонкой, а рост флуктуаций — медленнее или его пет вообще. Однако, когда пленка становится топкой, скорость истечения жидкости уменьшается, а флуктуации, если они есть, быстро растут до тех пор, пока толщина нлепкп не достигнет критического значения. Экспериментальная проверка этой теории показала [163], что утончение происходит быстрее, чем предсказывает теория, а критическая толщина пленки несколько меньше теоретического значения, по-видимому, вследствие неровности ее поверхности.
|
|
|
|
В уравнение (4.59) входит неопределенная величина (длина волны X), поэтому на основе теории флуктуационных волн А. Шелудко с учетом скоростей роста прогиба и утончения всей пленки автором работы [163] получены уравнения, не содержащие величину К:
П » Рк
(4.60)
Где рк — капиллярное давление; /к — коэффициент.
В работе [81] отмечено, что изложенная теория разрыва пленок в основном соответствует экспериментальным данным. Однако в этой теории имеется ряд неясностей, объясним, которые еще не представляется возможным.
Иногда нестабильные пленки внезапно разрушаются при толщине, превосходящей несколько диаметров молекул. Например, нлепкп нз водных растворов спиртов и нсдпссоцпироиаи - ных жирных кислот разрушаются прн толщине 50 нм. Перед разрывом такие пленки достигают толщины, при которой быстро переходят в нестабильное состояние. Утончению нестабильных пленок не препятствуют силы отталкивания в двойном электрическом слое, и скорость их разрушения пропорциональна силам притяжения и обратно пропорциональна вязкости жидкости.
Механизм разрушения толстых пленок, рассмотренный выше, ие может быть отнесен к черным пленкам. Разрушение этих пленок протекает с образованием дырки [81, 165]. Б. В. Дсрягпн выделяет три стадии процесса разрыва пленки [165]: постепенное утончение всей пленки; скачкообразное появление отдельных участков, толщина которых меньше толщины всей пленки, и последующее расширение этих участков; образование в пленке отверстия, расширяющегося с большой скоростью.
Постепенное утончение пленки происходит в результате истечения из нее жидкости под влиянием гравитационных сил и сил всасывания в каналы Плато. Пленки толщиной ~0,1 мкм утончаются в результате взаимного влияния ван-дер-ваальсо - вых сил притяжения и сил отталкивания, возникающих в деой - Ном электрическом слое. При дальнейшем утончении нечото - рые пленки становятся метастабильньши, другие разрушаются при достижении толщины 0,05—0,01 мкм. Метастабнльность пленок проявляется при взаимном уравновешивании сил всасывания в каналы Плато, сил притяжения и электростатических сил отталкивания. Нестабильность пленок пен является следствием преобладания сил притяжения [163].
По теории разрушения черных пленок, разработанной Б. В. Дерягиным на основе теории гомогенной кавитации Я - Б. Зельдовича, первоначально происходит двухмерное растяжение пленки, подготавливающее и осуществляющее прорыв ее. Образующаяся в результате деформации дырка обусловливает разрыв пленки [165].
Дальнейшее развитие теории разрушения черных пленок Б. В. Дерягниа позволило вывести уравнение для вычисления вероятности изотермического прорыва натянутой пленки заданной площади за единицу времени [166]. Следует отметить, что экспериментальная проверка теории дырочного разрушения черных пленок не проводилась.
Представляют интерес исследования скорости разрушения пленки. Впервые этот процесс был изучен Дюпре, который рассчитал скорость разрыва и при допущении, что поверхностная энергия пленки полностью превращается в кинетическую энергию жидкости. На основании этого допущения уравнение баланса энергии имеет вид
2aS = ти*/2 = i/2S6p«2 (4.61)
Где Аир — поверхностное натяжение и плотность жидкости; т — масса пленки; S—площадь пленки.
Отсюда можно определить скороси» pa ipyiiienmi пленки:
Ы = /45/(рб) (4.62)
Согласно измерениям [167] скорость разрушения пленок составляет от 350 до 1500 см/с и остается постоянной в течение всего процесса разрыва пленки. Однако в этих исследованиях не учитывали кинетическую энергию образующихся прн разрыве капель. С учетом этого явления числовой коэффициент в уравнении (4.62), равный 4, оказался не соответствующим экспериментальным данным [168]. Значение этого коэффициента <1 для пленок толщиной 6<0,02 мкм и лишь при 6 = 0,1 мкм достигает постоянного значения, равного 2. Это объясняется тем, что поверхностная энергия не полностью превращается в кинетическую, а некоторая часть ее рассеивается. Скорость разру-
Ог шения пленкп уменьшается с увеличением толщины, а в области толщин 10 нм имеется максимум (~35 м/с).
Более точно описывает действительный процесс уравнение полученное при допущении, что скорость распространения круговой волны ик, действующая против сил поверхностного натяжения двухсторонней пленки, постоянна [171]:
Ик = /2о/(6р) (4.63)
Уравнение (4.G3) показывает, что скорость распространения волны в У2 раз меньше скорости, определенной по уравнению Дюпре.
При разрушении пленки в ее центральной части образуется круглое отверстие. В результате расширения этого отверстия перед краями фронта распространяется в виде окружности с увеличивающимся радиусом «ореол» [168], представляющий собой утолщенную область пленки. Поверхностная энергия первоначального отверстия пленкн площадью S равна 2So0, а кинетическая энергия определяется равенством
V2S6oP"K2 = So о
Таким образом, кинетическая энергия в два раза меньше поверхностной энергии, следовательно, рассеивается не менее 50% последней, как это экспериментально показапо в работе [169]. Значение числового коэффициента в уравнении (4.63), равного 2, подтверждено экспериментально [170]. С использованием допущения (4.63) можно рассчитать скорость разрыва. которая составляет 80—8 м/с для пленок с а=30 мН/м, р = = 1000 кг/м3 и 6 = 10—1000 нм.
Фронт волны фактически распространяется со скоростью, уменьшающейся в направлении от отверстия, поэтому имеет место некоторое отклонение от сгогношения (4.63).
Как уже отмечалось, разрыв нлсики сопровождается образованием капель, направление н скорость движения которых соответствуют параметрам фронта распространяющейся волны. Средний радиус капель, образующихся при разрыве пленки, практически не зависит от ее толщины и в интервале толщины пленки 0,58 1,16 мкм составляет 40—55 мкм [167].
Разрыв пленок пузырьков на водной поверхности имеет большое значение в природе и практической деятельности человека. Так, из капель, образующихся прн разрыве пузырьков на поверхности океана, в результате испарения воды возникают ядра конденсации, на которых конденсируется атмосферная влага (образование облаков). В результате разрушения пленок пузырьков на водной поверхности очистных сооружений содержащиеся в стоках микроорганизмы попадают в воздушную среду и распространяются на значительные расстояния от источника загрязнения.
• Как самостоятельный процесс разрыв пленок в объеме пены цсслсдован недостаточно. Известно, что Шварц, применявший
|
|
|
I. '1 |„ Нулевая ^ |
|
Линия |
|
|
|
Ifv. ■ч 1 |
Рис. 37. Осциллограмма, отображающая процессы, происходящие при нанесении пеиы на обрабатываемую поверхность и распаде
Пены.
Л соответствует: hi — кинетическое действие пены; A/i| и Дhi— втягивание частиц внутрь пеиы в течение 0,2 и 0,4 с; hi — разрыв пленки.
Для исследования пен акустический метод, обнаружил, что в стойких пенах в течение первых 30 мин их «жизни» разрыв пленок практически не происходит. Дальнейшим развитием работ Шварца явилось измерение шумовых свойств пеп в процессе их разрушения: звукового давления и интенсивности звука [171]. В качестве датчика использовали микрофон. С помощью усилителя на регистрирующем приборе фиксировалось звуковое давление по изменению напряжения в электрической цепи. Исследования показали, что в отличие от результатов работы Шварца малостабильные пены (опыты проводили с 0,02; 0,03; 0,05%-ными растворами лаурилсульфата натрия) разрушаются мгновенно (в начальный момент прибор фиксирует наибольшее звуковое давление, которое затем уменьшается). Звуковое давление обусловлено не только разрушением пленок, но и вибрацией пены при ее распаде. Пузырьки верхнего слоя пены при разрушении создают более сильное звуковое давление, чем давление от пузырьков, расположенных внутри пены. Это вызвано частичным поглощением звука пузырьками. С увеличением концентрации ПАВ в ненообразующем растворе звуковое давление и интенсивность звука при разрушении пены уменьшаются в связи с ростом ее стабильности.
Для изучения разрушения пленок в пене применяли также тснзомстрический способ [172]. Происходящие при разрушении процессы записывали на пленку осциллографа (рис. 37). На основании обработки большого числа осциллограмм были определены некоторые динамические усилия, возникающие в пене в момент нанесения пены и при ее распаде (в Н):
При втягивании частицы внутрь пены (капиллярное всасыва - 0,4-Ю-5 нне) в течение 0,2 с
То же в течение 0,4 с 2,5-10'5
При кинетическом воздействии пены в момент се нанесения 10,4-10~&
При разрыве пленок 9,4■ 10-^
Разрушение пузырьков в столбе пены происходит послс того, как закончатся процессы истечения и диффузии, а пленки пены достигнут критической толщины. По Манегольду вид распада определяется структурой пены и свойствами ПАВ. Уменьшение высоты столба пены связано с разрывом поверхностных пленок и изменяется во времени при логарифмическом распаде -
по уравнению, предложенному Мапегольдом:
Dh/dx = a (/i — Лпл) (4.64)
Где /(— высота столба пены и момент т; /1пл — высота столба междунлеиочиой жидкости; а—постоянная распада.
В результате интегрирования уравнения (4.64) получаем:
Где /i0 — начальная высота столба иены.
Если заменить высоту столба пены и жидкости их объемами и пренебречь объемом жидкости в пене, получим:
1°(VJV) — ах , (4.66)
Для пей нз растворов моющих веществ распад описывается уравнением
V0 — V=^a(ebl—) (4.67)
Где B — константа
Подтверждено соответствие этого уравнения фактическим данным, особенно в области
Значении т^б и мин.

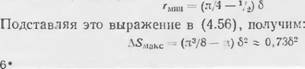

 Опубликовано в
Опубликовано в