ДИФФУЗИОННЫЙ ПЕРЕНОС ГАЗА
 3 декабря, 2012
3 декабря, 2012  admin
admin В соответствии с уравнением Лапласа давление в пузырьках воздуха обратно пропорционально радиусу пузырька. Так как пены практически всегда полидисперсны, давление в пузырьках пены не будет одинаковым. Разность давлений в пузырьках обусловливает диффузию газа из области высоких давлений (мелкие пузырьки) в область низких давлений (крупные пузырьки). Скорость диффузии пропорциональна разности давлений внутри пузырьков:
Pi — PZ = Др = 2ог(1/г1— l/rj при Г! О, (4.29)
А также проницаемости жидких пленок, разделяющих пузырьки различных размеров.
Днффузня газа приводит к тому, что маленькие пузырьки уменьшаются и в конце концов исчезают, а большие пузырьки растут. Таким образом, диффузия увеличивает полиднеперс - ность пен.
Рассмотрим процесс слияния двух пузырьков в один, исходя из физических превращений в этой элементарной системе. Поскольку общее количество газа при слиянии пузырьков не изменяется, па оспонапни уравнения Лапласа н газового закона pV=const можно записать:
(Риш - I - 2"//-,) Ч,Пг - I- (/Гиш - I 2<т/л.) Узлг*., - (/).,, „, -[- З. т/л,,) (4.30)
Или
Ратн (Л + г>2- Г312) + Со (г2! + га* _ г212) = 0 (4.31)
Где Г|2 — радпуе пузырька, образованного в результате слияния двух пузырьков радиусом г и г2.
Величины (г13 + г23—г123) н (Ri2+R22—Г122) можно выразить через нзмеиепие объема пузырьков AV и поверхности пленки жидкости AS в результате слияния пузырьков. Подставив вместо них соответственно 3AV/4n н AS/4n в уравнение (4.31), получим уравнение состояния пепы [158]:
З/ЭатмДУ -Г 2оД5 = 0 (4.32)
Которое аналогично приведенному рапсе уравнению П, В. Де - рягина (2.12).
Так как атмосферное давление раТм и поверхностное натяжение жидкости с могут быть только положительными величинами, то, чтобы удовлетворять условию (4.32), AV и AS должны иметь противоположные знаки. Следовательно, если при слиянии пузырьков происходит уменьшение поверхности раздела (AS<;0), то одновременно объем содержащегося воздуха в конечном пузырьке должен увеличиваться (AV>0).
Уравнение состояния пены (4.32) может быть использовано также к отдельным покоящимся пузырькам, однако оно неприменимо для всплывающих пузырьков (и некоторых типов иен), так как внешнее давление на всплывающий пузырек непостоянно н кроме атмосферного давления включает гидростатическое, т. е. p06vx = PaTM + pgh, где H — расстояние пузырька до зеркала жидкости.
В пенах, устойчивость которых невелика, переменными величинами являются р (при интенсивном истечении из пены жидкости) или h, когда происходит разрушение пленок в верхних участках столба пены.
В пене полиэдрического строения диффузионный перепое газа незначителен, поскольку пленки, разделяющие пузырьки, почти плоские. Но и для таких пен справедливо уравнение состояния. Так как газ в каждой ячейке пены находится под давлением р—ратм выше атмосферного, можно представить сферу радиуса г, которая содержит газ с тем же давлением, что и в ячейке с радиусом, соответствующим
Г = 2 о/(р — Ратм)
Эту воображаемую сферу Росс [153] назвал «сферой эквивалентной кривизны». Тогда можно принять, что объем и площадь поверхности ячейки многогранной формы соответственно равны
V = Ar» и S = b/2 (4.33)
Где а и B — константы, между которыми существует определенное соотношение. Учитывая поверхность сферы с внешней и внутренней стороны, а также равенство V/S=rl6 и используя уравнение (4.33), получим, что для любой ячейки пены 6а=Ь.
Общее количество газа в пене определяется уравнением состояния газов:
PV = nRT
Где п—число моль газа.
Количество газа во всех пузырьках пены можно выразить в виде суммы:
<4-34>
Где р/=р«тм + 2ст/г — давление внутри одного пузырька; 1',=о, т,3 — объем одного пузырька.
Используя соотношения (4.33) и (4.34), получим уравнение состояния пены:
PV + z/3oS = nRT (4.35)
Это уравнение представляет собой интегральную форму выведенного выше выражения (4.32), которое в свою очередь эквивалентно уравнению Б. В. Дерягнпа (2.12).
Механизм диффузионного переноса газа в пене впервые был изучен Кларком и Блэкманом. Полагая, что диффузия газа между пузырьками пропорциональна выражению
Dn/dx~ 2а (1/Гмш, - 1/7) (4.36)
Где dn/dx— скорость изменения числа молекул газа в пузырьке; г и гМПн — средний и минимальный радиусы пузырьков соответственно.
■авторы использовали уравнение диффузии в форме
Dn/ix = —4nr-G-2a (1 /ГЫШ1— 1/7) (4.37)
Где G — коэффициент, характеризующий скорость диффузии молекул газа через единицу поверхности пузырька при давлении I мН/м2. Этот коэффициент определяется экспериментально; выражается в единицах измерения моль-м2/(см2-Н).
При выводе уравнения (4.37) авторы использовали допущение о том, что диффузия газа протекает через поверхность контакта фаз, равную поверхности наименьшего пузырька 4пг2иин. Уравнение состояния газов для р = ратч + 2о/г (давление в пузырьке) при условии постоянства температуры можно записать в виде
VAp-f pAV = bnRT (4.38)
При уменьшении давления радиус пузырька увеличивается, и следовательно
Ар = —2оДг/г3 (4.39)
Подставив значения Ар н AV—4nr2Ar в уравнение (4.38), пренебрегая влиянием уменьшения давления на радиус пузырька [см. уравнение (4.39)], получим:
Р ■ 4 лгг Ar = AnRT (4.40)
Для получения выражения в дифференциальной форме, подставляя уравнение (4.40) в (4.37) и пренебрегая членом 2о/г<С «Сратм, имеем:
Dr/dx = 2aGRT/paTH- (1/г— 1/г) (4.41)
После объединения констант
К = 2 oGRT/paTa
Получим упрощенное выражение
Dr/dx = к (1/Г— 1/г) (4.42)
Приведенное уравнение характеризует изменение радиуса пузырька вследствие диффузии газа. Следует отметить, что из - за наличия радиуса г, который авторы рассматривают постоянным, применимость уравнения (4.42) ограничена, поскольку такое постоянство может иметь место лишь в узком интервале времени.
Де Фриз, применив к процессу переноса газа через пленку жидкости известное уравнение диффузии
—dn/dx = DSdc/dx
Где D — коэффициент диффузии; dcjdx — градиент концентрации диффундирующего вещее та.
Пришел к выражению, позволяющему определить радиус уменьшающегося во времени пузырька:
|
2___ |
|
Г |
|
0 Ратм |
4RT DoL
-g-(t-t„) (4.43)
Где / растворимость газа и жидкости ирн данном даилешш воздуха в пузырьке, определяемая экспериментально, моль-м*/(мМ1); б—голщнна пленки пузырька.
Для вывода уравнения (4.43) были приняты следующие допущения: поверхность пузырьков идеально сферическая; процесс диффузии стационарен, вследствие чего dc/dx = Ac/6', 2а/г<Ср.1т. м, т. е. капиллярное давление в пузырьке пренебрежимо мало. Эти допущения, безусловно, ограничивают область использования уравнения (4.43). Расчеты по этому уравнению дают лишь ориентировочные значения искомых величин. Примерные значения радиусов пузырьков воздуха в масляной эмульсии и латексе, вычисленные по уравнению (4.43), составляют 4-10 4 и 1,6-10~4 см соответственно [122].
В ходе старения иен наибольшим изменениям объема вследствие диффузии газа подвергаются пузырьки, имеющие наибольшую разность радиусов, поскольку между такими пузырьками разность давлений также наибольшая. Это хорошо видно
|
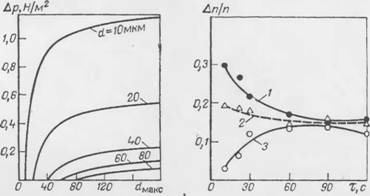
Рис. 33. Зависимость разности давления между малым (d) и большим (dMa4c) Пузырьками от duaKC. Расчет по уравнению г=2сЦр—ржти ) при о=30 мН/м. |
Рис. 34. Кривые распределения пузырьков некоторых фракций во времени.
Фракции пузырьков (по диаметру в мкм): 1 — 40—80; 2 — 120—160; 3 — 200—240. Кратность пены — 25. барботирование воздуха через 1%-пый раствор сульфонола 11П-1.
Из рис. 33, характеризующего изменение избыточного давления в маленьких пузырьках в зависимости от диаметра большого пузырька.
В полидисперсной пене имеется фракция таких пузырьков (по размеру), число которых остается постоянным по крайней мере в течение некоторого времени, несмотря па то, что диффузия газа протекает непрерывно. Радиус пузырьков этой фракции назван Манегольдом [1] критическим. Пузырьки, радиус которых меньше критического гкр, уменьшаются в результате диффузии. Объем пузырьков с г>гкр увеличивается. Представление о критическом радиусе пузырьков можно получить из рис. 34, который показывает изменение во времени доли пузырьков различных размеров. Как видно из рисунка, меньше всего изменяется содержание пузырьков диаметром 120—160 мкм. В этот интервал размеров, по-видимому, входит критический размер пузырьков.
Для нахождения математической зависимости, связывающей изменение числа пузырьков в единице объема пены во времени, очень важен экспериментально доказанный факт, что распределение пузырьков по размерам во фронтальном слое (т. е. внешнем слое, ближайшем к объективу фотокамеры) практически соответствует распределению пузырьков в объеме пены.
В работе [141] предложено математическое выражение для функции распределения пузырьков по размерам:
U-iZr*y <4-44>
Где а — параметр функции распределении.
Приняв в уравнении (4.44) т0=0, r0 = r't Г=О, т=т, получим:
/ ARTDoLx .
Общее число пузырьков Л'т (г - > " единице объема пепы и момент т=тг1 равно начальному числу пузырьков N0 (для т = 0), уменыненному на число пузырьков, исчезнувших за время v,<, что можно выразить соотношением [НЗ]
I
|
(4.46) |
|
F (/■) Dr |
-I
Интеграл в уравнении (4.46) после подстановки (4.44) приобретает вид
Г' г' г'
С с 6 аг Г Rdr
J (1 + ССГ*)* dr = 6a (1 +arV (4'47)
0 0 0
Интегрированием (4.47) получим:
Г'
|
= П л. (4-49) |
ГF(R)Dr - I--,, (1.48)
При подстановке в (4.46) найдем:
Ли.
'Т(Г')- (1 4- аг'2)
Или после подстановки (4.45) в (4.49):
N,
Л'т_ [1 - Ь 4RTDLaax/(pariMd (4'50)
Уравнение (4.50) можно представить как
Л; N° ь 4RTDLaa
Ъ-UTW k = Ратмб (4-51>
Экспериментально методом фотографирования определяют не число пузырьков в единице объема пены, а число нх проекций л, приходящихся на единицу площади поверхностного слоя. Функциональная зависимость п-—т может быть определена прн следующих допущениях [122]: параметр функции распределения и зависит только от времени; некоторый переходный коэффициент, характеризующий недостаток пузырьков во фронтальном слое по сравнению с числом пузырьков внутри пепы, пе зависит от времени. С учетом этих допущений было получено уравнение, характеризующее распределение пузырьков во фронтальном слое [141]:
|
81 |
Пх = «„/(1+Ат)2 (4.52)
(3—952
Использовав формулу (4.43) и предложенную Де Фризом функцию распределения пузырьков по размерам (4.44), П. М. Кругляков и II. Р. 'Гаубс вывели [115] уравнение, характеризующее изменение удельной поверхности раздела в иене но времени вследствие диффузии газа:
(5„ - 5Х)/5Т = V (4.53)
Эксперименты показали хорошее совпадение этого уравнения с теорией.
Для аналитического сравнения уравнений (4.43) и (4.53) выразим левую часть первого из них через поверхность пузырька, приняв в соответствии с рекомендацией Манегольда 6 = const. Тогда получим:
4RT DoL
SX = SB—ят; о=------------------------- с— = const (4.54)
Ратм 0
Это уравнение показывает, что сокращение поверхности уменьшающегося пузырька протекает линейно во времени. Суммарная поверхность раздела с течением времени также сокращается, однако в связи с ростом больших пузырьков в результате диффузии уменьшение суммарной поверхности раздела фаз протекает медленнее [соотношение (4.54) не учитывает влияния роста больших пузырьков на увеличение поверхности]. Если допустить, что увеличение поверхности больших пузырьков происходит также по линейному закону, то и общая поверхность раздела будет уменьшаться линейно во времени. Согласно уравнению (4.53) изменение общей поверхности раздела нелинейно, так как
S0/Sx = 1 + V
Отсюда следует, что или увеличение поверхности больших пузырьков происходит не по линейному закону, или различие в закономерностях изменения поверхностей раздела обусловлено различными свойствами пей, примененных для исследования.
Для формальной оценки процесса разрушения пен воспользуемся уравнением кинетики быстрой коагуляции аэрозолей М. Смолуховского:
(4-55>
Где V и v0— частичная концентрация дисперсной фазы в момент т и то=0 соответственно; Tj/2 — время, необходимое для снижения концентрации частиц в два раза.
При соответствии уравнению (4.55) зависимость обратной величины числа частиц всех размеров (l/2v,-) от времени должна быть линейной [161].
Для этого анализа были использованы данные, приведенные на рис. 16, а также результаты работы [162]. Поскольку зависимость l/2vi—х действительно выражается прямыми линия-
|
|
|
|
|
П |
|
2 3 и - г, мин |
|
Рис. 35. Зависимость обратной величины числа ячеек в единице объема пены От времени. / — данные рис. 1С; 2 — дяннме по [1С2]. |
|
|
|
Толщина лленки |
Рис. 36. Увеличение поверхности раздела при разрыве пленки [1411.
Ми (рис. 35), можно считать, что суммарный процесс разрушения пей формально подчиняется кинетическим уравнениям реакции второго порядка по крайней мере в течение первых 5 мин существования пены.


 Опубликовано в
Опубликовано в