ФАКТОР УСТОЙЧИВОСТИ, ОБУСЛОВЛЕННЫЙ ЭФФЕКТАМИ МАРАНГОНИ И ГИББСА
 3 декабря, 2012
3 декабря, 2012  admin
admin Тонкие пленки обладают способностью реагировать па локальные изменения толщины, вследствие чего происходит как бы «залечивание» ослабленного участка. Это «залечивание» происходит за счет поверхностного течения раствора из области низких поверхностных натяжений в область больших значении о (эффект Марангони), поскольку прн утончении пленки происходит увеличение о, т. е. молекулы ПАВ поверхностного слоя находятся как бы в состоянии разрежения. Возможен и другой путь самовосстановления пленки — в результате миграции молекул ПАВ из объема раствора к поверхностному слою.
Некоторые авторы [86] эффект Марангони называют «вязкостью расширения», величина которой
R)d = A oS(dS/dT)-i (3.5)
Равна изменению поверхностного натяжения, отнесенному к относительной скорости изменения площади адсорбционного слоя.
|
49 |
Миграция молекул из объема раствора к поверхности не может обеспечить прекращения утончения пленки, так как прн этом отсутствует поверхностный перенос. Кроме того, необходимо время для достижения молекулами ПАВ поверхностного слоя, которое составляет, по данным работы [111], 0,001—0,1 с. Число молекул ПАВ в жидкой части пленки часто бывает недостаточным для полного восстановления начальной концентрации ПАВ в поверхностном слое. Поэтому даже после достижения равновесия вследствие местного восстановления в поверхностном слое пленки может оказаться недостаток молекул ПАВ, что приводит к сохранению избыточного (но сравнению с нер-
4—952
Воначальным) поверхностного натяжения ослабленного участка [112].
Количественно эффект Мараигопп был изучен па гримере системы изобутанол — вода 1ПЗ]. Максимальная скорость восстановления ослабленного участка пленки пены под действием поверхностных енл проявляется в области, непосредственно примыкающей к источнику поверхностного движения раствора (капиллярная трубка, из которой вытекает изобутанол), й постепенно убывает с удалением от этого источника. Время, необходимое для завершения поверхностного течения, составляет несколько сотых долей секунды.
Согласно работе [113] поверхностное движение молекул обусловлено напряжением сдвига Р, возникающим под действием градиента поверхностного натяжения:
P = da/dr (3.6)
Где г — радиальное расстояние от точки возникновения возмущения.
Так как локальный градиент поверхностного натяжения возникает под действием локального градиента концентраций, то
Da/dr = da/dc-dc/dr (3.7)
Величина da/dc при постоянной температуре определяется поверхностно-активными свойствами растворенного вещества и его концентрацией. Радиальный градиент концентраций dc/dr Учесть крайне трудно, однако качественно можно представить, что он пропорционален разности концентраций в поверхностном слое:
Dc/dr ~ Ас
Отсюда следует, что скорость поверхностного течения V в общем виде является функцией
V — F (Acda/dc) (3.8)
Показано [114], что эта функция имеет вид
V = k Acda/dc (3.9)
Где к — коэффициент пропорциональности, в условиях эксперимента [114]
Область значении величины Acda/dc для системы изобутанол — вода составляет (4—16)10 J Н/'м.
Уравнение (3.9) показывает, что скорость процесса восстановления утонченного участка тем выше, чем большую поверхностную активность проявляет ПАВ и чем больше разность концентраций в утонченном и «здоровом» участках пленки.
Эффект Марангони зависит также от объема жидкости, прилегающей к поверхностному слою: по мере уменьшения объема жидкости этот эффект должен возрастать. При утончении пленки роль эффекта Марангони усиливается, однако для пленок очень малой толщины, состоящих практически нз двух сольва- тированных слосн, шшмнне этого эффекта пезпачпелыт, поскольку в адсорбционном слое разрежение «частокола» молекул ПАВ краппе затруднительно. Таким образом, влияние эффекта Марангони на стабильность пленки максимально ври некоторой оптимальной ее толщине.
Длительное время эффект Марангони рассматривали совместно с эффектом Гиббса. Лишь с СО-х годов механизм их действия рассматривается раздельно.
Стабилизация пленок, по Гпббсу, объясняется возникновением локальных разностей поверхностного натяжения под влиянием механических пли термических возмущении, вызывающих растяжение пленки. Поверхностное натяженпе растянутой части пленки возрастает, поскольку увеличение новерхпостп пленки приведет к уменьшению средней концентрации ПАВ в поверхностном слое. Локальная разность поверхностных натяжений п пленке обусловливает возникновение потока молекул ПАВ в абсорбционном слое в сторону более низкой концентрации — к растянутой части пленки.
Основой теории Гиббса является предположение об упругости пленки, для количественной характеристики которой он ввел понятие модуля упругости. Прн растяжении пленки в результате повышения поверхностного натяжения проявляется ее упругость, силы которой приводят как бы к обратному сокращению этой пленки.
Упругость (эластичность) пленки Е по Гпббсу определяется отношением увеличения поверхностного натяжения к относительному приращению ее площади dS/S в результате местпою расширения:
Е = ISda/dS (3.10)
Прн выполнении условия Е>0 пленка устойчива к любым локальным возмущениям, поскольку силы упругости способны предотвратить разрушающее действие возмущений и г. ернугь ее в исходное состояние. Разрушение пленка под действием возмущений возможно, если она превратилась в тонкую, средняя часть которой утратила свойства жидкости в массе.
По уравнению адсорбции Гпббса
1 Da
L^2RT dine (3,II)
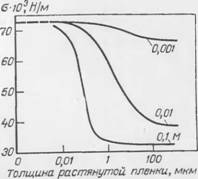
В работе [115] рассчитано поверхностное натяжение растянутых до различных толщин плепок, содержащих додецнлеульфат натрия в концентрациях 0,001, 0,01 и 0,1 моль/л. Полученные результаты (рис. 27) показывают, что интервал толщин пленок, на который распространяется действие эффекта Гпббса, зависит от концентрации ПАВ в растворе. При низких концентрациях ПАВ упругость пленок не проявляется, так как уменьшение п очень незначительно. При наибольшей концентрации (в данном случае 0,1 моль/л) пленки проявляют при толщинах более 1 мкм
|
|
Рис. 27. Изменение поверхностного натяжения тонких пленок раствора доде - цнлсульфата натрия в зависимости от их толщины при различной концентрации ПАВ [115].
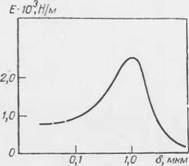
Рис. 28. Зависимость эластичности пленки но Гпббсу от ее толщины [ПС].
Также незначительную эластичность как вследствие малой зависимости поверхностного натяжения от концентрации додецил - сульфата натрия, так и из-за большого запаса ПАВ в объеме раствора. Эта концентрация обеспечивает получение упругих пленок в области толщин 0,1—0,01 мкм. И только при содержании 0,2 моль/л додецилсульфата натрия образуются пленки, обладающие значительной эластичностью в широком интервале толщин. Отсюда видно, что эффект Гпббса имеет важное значение как фактор стабилизации только для топких пленок и при сантнмолярных концентрациях растворов ПАВ.
Предсказываемая теорией зависимость эластичности пленок от их толщины и состава раствора подтверждена расчетным путем [116]. Наличие у пленки, содержащей ПАВ, упругих свойств обосновано аналитически, поскольку выполняется условие £>0 [81].
Китченер [116] принял, что при исходной концентрации раствора с0 в средней части пленки толщиной 6 концентрация ПАВ составляет с' при условии равновесия с поверхностными слоями. Эта концентрация определяется по уравнению
С' = с0 — оГ/б (.12)
Где а — коэффициент.
|
|
С помощью уравнения (3.12) и изотермы адсорбции можно найти функцию с' в зависимости от б. При известной с' по изотерме поверхностного натяжения определяется функция а в за - - внсимости от толщины пленки, а затем графическим дифференцированием — эластичность как функция толщины. Из рис. 28 следует, что максимальной эластичностью обладают пленки толщиной — 1 мкм. Метод был откорректирован введением члена Го/6о, относящегося к исходному раствору [116].
При условии равновесия между пленкой жидкости н ее элементом поверхностное натяжение изменяется в соответствии с уравнением Гиббса:
П
—Da = RT V p. rf |n у. С( (3.131
Где Г/, V'i — соответственно величина адсорбции и коэффициент активности i-ro компонента; it — объемная концентрация 1-го компонента.
Измснеппе площади поверхности элемента пленки пропорционально изменению ее толщины и может быть выражено [117] уравнением
—U In S U 1и б = (бUct + 2JI'j)/2l'j (3.14)
Из уравнений (3.10), (3.12) и (3.13) получим выражение для модуля эластичности пленки по Гиббсу:
Лот V г'3 1 + <Лпу, АЛпс,
E=4RT У, Т,------- б + 2dV{/dci 15>
(=2
Следует отметить, что уравнение (3.15) было получено при некоторых допущениях, вносящих погрешности в искомую величину, особенно в применении его к тонким пленкам. Более строгая теория упругости пленок с использованием метода конечной толщппы применительно к плоекопараллельным пленкам была развита А. И. Русановым, который получил уравнение для моду.'Iя равновесной упругости:
1 г,2
V 1 ' (")_____________ 1 -f d In уT/D In cj__________
E = f~i (6 - 2Л6) (1 d In Сл/d r. Ci) + 2dVivl)/<lCi (3J6)
Где Г,/„) - относительная адсорбцм н I-io компонента; с« — копией 1рлты //-го кимпиисига (растворителя).
Уравнение (3.15) отличается от уравнения (3.16) поправками 2Д6 и (1—d In Сл/сИп с,). Значение первой нз них зависит от толщины нлснкн, и при больших толщинах ею можно пренебречь, так как Дб<Сб. Значение второй поправки определяется концентрацией компонентов и для очень разбавленных растворов близко к единице [118].
Тот факт, что в работе [119] не выявлена зависимость эластичности пленки от ее толщины, объясняется, по-видимому, значительным вкладом в эластичность неравновесной упругости вследствие эффекта Марангони. Результаты измерения эластичное in нлснкн ио усовершенствованной методике, исключающей эффект Марангони [120], подтвердили наличие обратной зависимости эластичности пленки от ее толщины [см. уравнение (3.15)]. Однако измерения проводили только с использованием растворов, концентрация которых была близка к ККМ или превышала ее в три раза. В работе [118] с помощью специальной
5.3
Установки одновременно измеряли натяжение, площадь п толщину горизонтальной пленки, в которой исключалось влияние истечения междупленочной жидкости. Эластичность пленки рассчитывали по уравнению
Е& = V2(/2-/1) (3.17)
Где Е6—эластичность локального участка пленки; Fi и f2. 61 н бг — соответственно натяжение н толщина пленок в двух близких состояниях 1 и 2 (6— от 1 до 10 мкм).
Эластичность пленок, выражающаяся в противодействии дальнейшему увеличению поверхности и стремлении восстановить начальное равновесие, обусловливает определенное количество энергии, необходимой для расширения поверхности даже при постоянном значении поверхностного натяжения. Изменение поверхностной энергии составляет
ДГ = ОЛ5+(5+ А5)ЛО (3.18)
Для оценки относительных значений первого и второго членов уравнения (3.18) рассмотрим два случая: приращение поверхности пленки незначительно или оно велико и сравнимо с площадью пленки.
При AS<cS уравнение (3.18) превращается с учетом уравнения (3.10) в
DF = odS - f Sda = (а + VaЈ) dS (3.19)
Относительный вклад эффекта Гпббса согласно работе [121] определяется величиной Е2а. Относительное увеличение площади поверхности пленки dS/S можно заменить относительным увеличением площади, приходящейся на одну молекулу data, А изменение поверхностного натяжения Do—на изменение поверхностного давления dps, которое легко определить экспериментально. Тогда можно записать:
%Е = Sda/dS = —adpjda (3.20)
(знак минус обусловлен тем, что прн увеличении а уменьшается давление пленки).
Из уравнения (3.20) видно, что эластичность пленки можно рассчитать по результатам измерения площади, приходящейся на одну молекулу, в зависимости от давления. Экспериментально показано [122], что —adps/da = 0,5 £ = 50н-125 мН/м для конденсированных адсорбционных слоев многих ПАВ. Поэтому вклад поверхностной эластичности пленки Е/2о будет в 2— 3 раза превышать изменение поверхностной энергии вследствие увеличения площади поверхности при о=30—40 мН/м.
Во втором случае, когда величина деформации пленок пены соизмерима с ее площадью, AS = S и уравнение (3.18) принимает вид
AF — (о - f 2_с) S (3.21)
Вследстппе мгновенного расширения локального участка поверхности и. кики и два раза поверхностная коннешрация молекул ПАВ уменьшается также в два раза. Гкшсрмюсиюс натяжение на данном участке, зависящее от поверхиостпоп активности компонента, увеличивается, по не настолько, чтооы значительно изменить разность между начальным поверхностным натяжением пленки и поверхностным натяжением растянутого участка Go—о В этом случае вклад эффекта ГпСбса равен 2Д0/0=2(0О—о)/о. Прн низких концентрациях Г1АВ отношение ( 2(0о—0)/о<1. С увеличением поверхностной концентрации Г1ЛВ это отношение возрастает до ~2 (для растворов, которые имеют 02^ 1/2онао).
Из обсуждения видно, что в обоих предельных случаях вклад в увеличение поверхностной энергии за счет изменения поверхностного натяжения являетя величиной того же порядка, что н вклад за счет увеличения площади поверхности. 13ез - условпо, данный вывод справедлив только в случае если скорость деформации пленки превышает скорость установления равновесия в деформируемой пленке.
При возникновении разности поверхностных натяжений па отдельном участке пленки одновременно появляется и разность двухмерных давлений ps—P's>0, которая вызывает внутри пленки потоки жидкости в направлении, противоположном всасыванию жидкости в каналы Плато, что обеспечивает «подпитывание» тонкого участка пленки. Это равносильно тому, что жидкость вытекает из центральной части пленки в каналы Плато с меньшей скоростью. Таким образом, местная разность двухмерных давлений препятствует утончению пленки. В соответствии с этим течение междупленочпой жидкости можно представить как течение в плоском капилляре (см. гл. 4).
Локальные возмущения в пленке, вызывающие ее утончение и образование области повышенного поверхностного натяжения, создают градиент поверхностного натяжения, следствием которого является быстрое движение мопомолекулярпого слоя. Этот слой при движении увлекает с собой значительные количества жидкости пз нижележащего раствора, участвующего в восстановлении утончающейся области пленкн. Явление, названное поверхностным переносом, по мнению авторов работы [12.4], способствует стабилизации пленки, так как в утонченный участок поставляется дополнительный для «залечивания» материал. Модель поверхностного переноса предусматривает два допущения: стационарность поверхностного течения н отсутствие его на другой стороне пленки. Однако работой В. В. Кротова и А. И. Русанова [124] достаточно убедительно показано, что отмеченные допущения в общем случае механического или теплового возмущения не могут быть реализованы н справедливы лишь в некоторых условиях. Тем не менее теорию поверхностного переноса можно рассматривать как дополнение к эффекту Марангони, которая, учитывая этот эффект, указывает также,
Что под действием градиента поверхностного натяжения приводятся в движение прилегающие слои жидкости.
В опытах Шульмана н Теорслла мопомолекулярнын слон олеиновой кислоты распространялся со скоростью 5 см/с и увлекал за собой слой раствора толщиной 0,03 мм, которая не зависела от скорости новерхиостиого движения, но являлась линейной функцией вязкости нижележащего раствора. Однако эти данные следует рассматривать только как ориентировочные.
Рассмотренным выше фактором устойчивости нельзя полностью объяснить стабильность пен, так как он является определяющим только для малоустойчивых пенных структур.

 Опубликовано в
Опубликовано в