Оценка степени уноса материала электрода
 5 августа, 2016
5 августа, 2016  admin
admin Унос материала электрода (меди) при движении по нему приэлек - тродного пятна происходит всегда. Это, по-видимому, связано с природой приэлектродных процессов на "холодных” электродах. Но даже в тех случаях, когда имеются значительные следы оплавления материала электрода, этот унос может быть небольшим и удовлетворять требованиям достаточно длительной работы электродов. Однако при больших значениях силы тока существует некоторое пороговое значение скорости движения дуги. Если скорость перемещения приэлектродных пятен окажется меньше этого порогового значения, то унос материала электрода резко возрастает. В этом случае температура поверхности в пятне достигает температуры испарения и происходит сублимация материала. Значительный унос может происходить и за счет плавления, но, как нам представляется, только в тех случаях, когда перед набегающим пятном электрод нагрет почти до температуры плавления за счет предыдущих пробеганий дуги.
Из изложенного следует, что диаметр электрода, толщина стенки и интенсивность ее охлаждения должны быть выбраны таким образом, чтобы температура Г, рассчитанная по формуле (8.12), не достигла
температуры плавления, т. е. должно выполняться неравенство 7* +
+ Г < Г. Величину магнитного поля следует подбирать таким об-
разом, чтобы дуга двигалась с достаточной скоростью и сумма температур (см. формулу (8.1)) и Т не достигала температуры испарения материала электрода, т. е. должно выполняться неравенство
2 исп
где 7* - температура охлаждающей воды.
Проведем оценку степени уноса материала электрода в случае, когда в приэлектродном пятне достигается температура испарения. Точность оценки будет вполне достаточной, если для решения этой задачи воспользоваться интегральным методом, разработанным Гудменом. Будем считать, что температура нагрева некоторого слоя вблизи поверхности электрода от предварительных пробеганий дуги равна
7*00 = Tq + ^ Нагрев в пятне до достижения температуры испарения
Т РассматРиваем как нагРев полубесконечного тела, имеющего начальную температуру 7^ В дальнейшем на границе устанавливается
температура испарения и часть удельного теплового потока идет на испарение металла. Таким образом, выполняется граничное условие
л dT ds /n <ov
ч*ИГ ■ (8-|3> где s - граница испарившегося металла, г - удельная теплота испарения.
Гудмен рассмотрел также случай, когда граница имеет нулевую температуру. Это затрудняет пользование конечными формулами. Поэтому повторим все рассуждения автора, приняв распределение температур в общем виде:
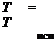
![]()
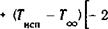
![]()
![]()
![]()
![]() (X-S)2 1
(X-S)2 1
/" о2 - I
(o-s)
Здесь 8 - толшина прогретого слоя.
При * = s = - -2- (Т - Т ), ах О-s исп ОО
откуда граничное условие (8.13) дает
. 2МТ - Т )
рГ as _ . ___ исп оо _ . 2
q dt (b-s)q $
Здесь
t _ (8-s)q
K МТ - Т ) '
ИСП ОО
Уравнение теплопроводности в интегральной форме имеет вид
4-(9-Г , .-S£l-) .-SL,
dt оо л д где
![]() 8
8
6 = I Tdx =
s
После подстановки в в уравнение (8.16) получим
Г
![]() 8-s d(8-s) 8-s оо, и rfs
8-s d(8-s) 8-s оо, и rfs
— ~dt------------- 7Г т - г <" -
ИС П ОО
где
ар г АГ
Подставив из уравнения (8.15) в уравнение (8.17), после ин
тегрирования найдем зависимость времени от параметра £:
♦ 2(1 - »)1п ]■ (8.18)
Уравнения (8.15) и (8.18) дают связь степени уноса и времени действия источника интенсивностью q, начиная с момента достижения
температуры испарения. В момент достижения температуры испарения s = О
V
t - ------------ Н--------- = о
*0 МТ - Г ) А
ИСП ОО
так как глубина прогрева для выбранного профиля температур 2(Г - Г )
0 ИСП ОО
Удобно время т сравнивать с временем действия источника до достижения температуры испарения г, которое связано с температурой испарения соотношением
тг(Г - Г )2Л2
![]()
![]() ИСП ОО
ИСП ОО
, 2 Aaq
от относительного времени действия источника после достижения на
7
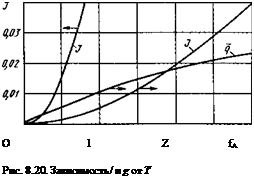
поверхности температуры испарения —------- приведена на рис. 8.20.
исп
Полученная зависимость дает четкое представление о темпе нарастания уноса материала электрода, если в пятне достигнута температура испарения и какое-то время т после достижения температуры испарения пятно еще находится над рассматриваемой точкой поверхности электрода. Допустим, что температура испарения достигается в некоторой точке приэлектродного пятна, тогда темп уноса нарастает от
g = 0 в этой точке до g на краю источника и общий унос из пятна составит
d гд
G = / gddx = / gdvdr dx = vdr.
X о
неп
J,9
0,3
О/
Здесь пятно считается условно квадратным со стороной, равной d:
![]()
![]() d - х d - vt
d - х d - vt
неп неп
т =------------------- =-------------------
Д V V
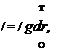 |
|||
Обозначив
окончательно получим
Для удобства расчетов проведем интегрирование приведенной на
рис. 8.20 зависимости и построим интеграл / в функции т. Резуль-
д
таты расчета приведены на рис. 8.20. Теперь секундный унос материала электрода может быть определен по простой формуле (8.22).
Порядок расчета по этой формуле следующий. Определяется температура = Г + 7*2> где 7"2 вычисляется по формуле (8.12).
Рассчитывается время достижения температуры испарения т по
формуле (8.19). Определяется безразмерное время пребывания источника над электродом после достижения температуры испарения
д VT
исп
По кривым рис. 8.20 находится интеграл /, и по формуле (8.22) определяется секундный унос материала электрода.
Приведем пример расчета по предложенной методике и сравним результат с данными работы [6]. Расчет проводится для катода,
8 2
поэтому AU = 7В. / = 210 А/м, скорость перемещения пятна v =
8 2
= 10 м/с. При этом тепловой поток в пятне q = AUj = 14-10 Вт/м.
—3
При силе тока / = 750 А диаметр пятна dQ = 2,2-10 м и время
Рис. 8.21. Зависимость степени уноса меди в
с катода от силы тока: I
А — по данным работы [б]; --------------- расчет
8 6
прохождения пятна над рассматриваемой точ-
^0-4 *
кой катода т = ---------- = 2,2*10 с. Время
2
действия источника, рассчитываемое по формуле (8.19) и необходимое для достижения температуры испарения, также равно о zoo т воо г, А
—4
2,2*10 с. Такое совпадение говорит о достижении граничной силы тока / = 750 А. При меньшей силе тока согласно предложенной методике унос должен отсутствовать. Принимая большую силу тока, например / = 800 А, определяем диаметр пятна и время т = -4 —
= 2,26*10 с. Определив т = 0,026 и сняв с рис. 8.20 значение —4 Д
/= 0,4*10 , по соотношению (8.22) определим унос меди G = = 1,45* Ю-4 кг/с.
Эксперимент показывает более плавное нарастание уноса с увеличением тока (рис. 8.21). Это, по-видимому, связано с неравномерной скоростью перемещения пятна.

 Опубликовано в
Опубликовано в