Пластины, как и стержни, являются системами с распределенными постоян­ными и имеют множество собственных частот. Простейшая модель - круглая пла­стина, определенным образом закреплен­ная по периметру и возбуждаемая в центре

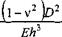
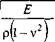
0,01 0,1 Аг, мм 1,0

сосредоточенной гармонической силой. Пластина совершает поперечные (изгиб - ные) колебания.

Существуют решения для жесткоза - щемленной по периметру, опертой по пе­риметру и свободной на краях пластины [305]. Жесткое защемление исключает возможность смещения и изгиба на краях пластины. Для этого случая входной ме­ханический импеданс пластины в пренеб­режении потерями чисто реактивный. Для частот ниже основной собственной часто­ты он представляется в виде [203, 305, 312]

Z =jX=j (со/иэ - 1/аКэ), (1.51)

где тэ - эквивалентная масса; К3 - эквива­лентная гибкость пластины.

Для круглой, жесткозащемленной по контуру пластины

тэ = 0,15 т;

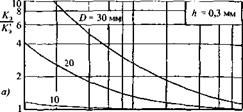
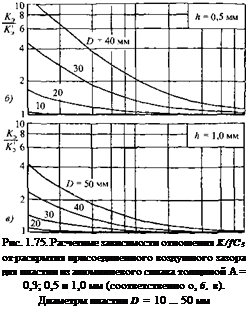
где т - физическая масса пластины; D - ее диаметр; А — толщина пластины; Е - мо­дуль Юнга; v - коэффициент Пуассона.

Основная собственная частота за­щемленной пластины [305]

(1.52)

На частотах / </і пластина имеет уп­ругое сопротивление. Кроме основной имеются более высокие собственные час­тоты, не кратные основной частоте (обер­тоны). При переходе через собственные частоты пластины характер реактивной составляющей ее импеданса меняется (с упругого на инерционный и обратно).

При представлении зоны дефекта ти­па расслоения моделью в виде защемлен­ной пластины между отделенным дефек­том слоем и внутренней частью конструк­ции обычно имеется заполненный газом зазор. Его толщина намного меньше дли­ны волны, поэтому он представляет собой сосредоточенную гибкость[203]

KT=l6V/pTc2S2,

где V - объем зазора; рг - плотность газа; сг - скорость звука в нем; S - площадь за­зора.

При средней толщине зазора А, = VIS круглой пластины диаметром D

КТ = 64АГ/ рг cTnD2.

Результирующая гибкость, образо­ванная соединенными узлом элементами К, и КГ, равна

К'Э = К3КГ/(К3+КГ).

На рис. 1.75 представлены расчетные зависимости отношения KJ К'э от раскры­тия А, газового (воздушного) зазора для защемленных круглых пластин различно­го диаметра и трех значений А толщины пластины.

1.12.

Формулы для расчета моментов инерции сечений и собственных частот изгибных колебаний свободных стержней [18]

1.13. Значення коэффициентов 7Гв(0,2) и 7Гв(1,0) для расчета собственных частот изгибных колебаний круглых пластин [18]

1.14. Значения коэффициентов Ks для планарных колебаний круглых пластин и поправки на толщину А [18]

Таким образом, воздушный зазор уменьшает эквивалентную гибкость пла­стины и, следовательно, увеличивает мо­дуль упругой составляющей ее импеданса. Это неблагоприятно сказывается на обна­ружении дефектов низкочастотными аку­стическими методами, в частности импе - дансным (см. разд. 2.5).

Собственные колебания свободных пластин (т. е. не закрепленных по пери­метру) можно разделить на [18]:

• колебания, формы которых анти­симметричны относительно средней плос­кости пластины (изгибные колебания);

• колебания, формы которых симмет­ричны относительно указанной плоскости - планарные или радиальные колебания.

/,(0.3)

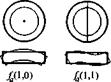
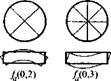
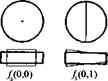
Рис. 1.76. Характер деформаций
круглых пластин на низших собственных
частотах [18]

Для круглых пластин (дисков) низ­шие формы колебаний характеризуются деформациями, показанными на рис. 1.76. Изгибные колебания обозначены /„ {т, и), планарные — fs (т, и), где т - число узло­вых окружностей', п - число узловых диа­метров.

Собственные частоты изгибных коле­баний представляются в виде [18]

г ( ч Ка Е

D V р

где D - диаметр пластины; Ка (т, п) - без­размерный коэффициент, представленный в табл. 1.13 для различных значений ко­эффициента Пуассона v и отношения hID (h - толщина пластины).

Собственные частоты различных мод планарных колебаний рассчитывают по формуле

W Ks Е

sV ’ Dp

где Ks(m, п)- безразмерный коэффициент.

В отличие от Ка{т, и), при малых значениях hID коэффициент Ks(m, п) зави­сит только от одного параметра - V. Одна­ко влиянием толщины можно пренебре­гать лишь при h/D < (0,25 ... 0,3). Для мо­ды 5(0,0) следует вводить поправки, начи­ная с h/D <0,1, так как экспериментальные значения частот будут заметно зани­
женными по сравнению с расчетными. Значения АД0, и), а также положительной поправки Д к АД0, 0) приведены в табл. 1.14.

Собственные частоты изгибных ко­лебаний тонких квадратных пластин со свободными границами рассчитывают по формуле

f,=K, ha~2 - , (1.55)

V Р

где а - сторона квадрата.

Моды колебаний таких пластин и значения безразмерных коэффициентов К, приведены в табл. 1.15.

Влияние нагрузки. Нагрузка актив­ным механическим сопротивлением уве­личивает потери колебательной системы, что приводит к снижению добротности и росту логарифмического декремента зату­хания.

Если добротность системы достаточ­но велика (Q > 10), изменение R практиче­ски не сказывается на собственных часто­тах конструкции. При меньших значениях Q увеличение потерь несколько снижает эти частоты. Изменение реактивной со­ставляющей X импеданса нагрузки суще­ственно влияет на собственные частоты. Характер этого влияния зависит от знака (инерционность или упругость) и структу­ры конструкции. Инерционная нагрузка снижает собственные частоты, упругая повышает.

В качестве примера рассмотрим из­менение основной собственной частоты