1.4.1. Основные понятия

Детали, узлы и готовые изделия мо­гут совершать механические колебания, т. е. представляют собой колебательные системы. Измерение параметров этих ко­лебаний позволяет оценивать качество колеблющихся объектов, в частности су­дить о наличии тех или иных отклонений от заданных свойств. Это дает возмож­ность использовать анализ колебательных характеристик для неразрушающего кон­троля.

Различают колебательные системы с сосредоточенными и с распределенными

постоянными.

Элементы системы с сосредоточен­ными постоянными - масса, упругость и активное сопротивление. Предполагается, что каждый из этих элементов обладает только каким-либо одним из упомянутых свойств. Это является идеализацией, так как в общем случае реальные элементы этому условию не удовлетворяют. Напри­мер, элемент упругости - пружина - все­гда имеет определенную массу, а элемент массы, например гиря, обладает некото­рой упругостью. Тем не менее, в опреде­ленных условиях такая идеализация до­пустима и полезна. Простейший пример - подвешенный на пружине груз, погружен­ный в вязкую среду. Здесь пружина пред­ставляет собой упругость, груз - массу, а сопротивление движению груза в вязкой среде - элемент трения. В системах с со­средоточенными постоянными колебания элементов массы и упругости происходят относительно положений их равновесия и не распространяются в окружающую сре­ду. Если такая передача и наблюдается, то она учитывается лишь как вносимые в систему потери на излучение.

В действительности элемент массы не является материальной точкой, а пред­ставляет собой тело конечных размеров, которое обладает не только массой, но и определенной упругостью. Деформация такого тела сопровождается потерями на внутреннее трение. Следовательно, в об­щем случае одно и то же тело имеет массу, упругость и активное сопротивление, ко­торые неразрывно связаны между собой и не могут быть разделены. Системы, где каждый элемент рассматривается как об­ладающий всеми тремя из названных ха­рактеристик, разделить которые невоз­можно, называются системами с распре­деленными постоянными.

В отличие от описанных ранее коле­баний упругой среды далее рассматрива­ются колебания систем, хотя здесь неиз­бежны некоторые повторения.

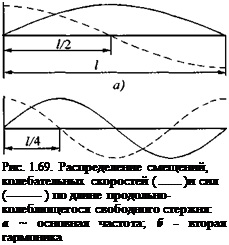
Если в какой-либо точке упругой среды действуют переменные силы, то в этой среде возникают переменные дефор­мации, смещения и напряжения, которые распространяются от точки возмущения в виде упругой волны, движущейся с опре­деленной скоростью в пространстве. Та­ким образом, колебания происходят не только во времени, но и в пространстве. При этом частицы среды колеблются от­носительно положения равновесия. Про­стейший пример колебательной системы с распределенными постоянными - тонкий длинный продольно колеблющийся стер­жень.

Во всех колебательных системах мо­гут наблюдаться вынужденные и свобод­ные колебания.

Вынужденными называют колебания, обусловленные действием внешней при­ложенной силы. Вынужденные колебания могут быть гармоническими (синусои­дальными), негармоническими (например, вибрация) или импульсными. После при­ложения возмущающей силы амплитуда колебаний устанавливается постепенно (переходный процесс). Время переходного процесса зависит от параметров колеба­тельной системы. С окончанием действия внешней возмущающей силы режим вы­нужденных колебаний прекращается и начинается режим свободных колебаний.

Свободными называют колебания, совершаемые системой после окончания действия возмущающей силы или систе­мой, выведенной из состояния равновесия и предоставленной самой себе.

Свободные колебания происходят на собственных частотах, значения которых определяются параметрами колебательной системы. Системы с сосредоточенными постоянными с одной степенью свободы (груз на пружине, маятник) имеют одну собственную частоту, более сложные сис­темы - несколько таких частот, а системы с распределенными постоянными - мно­жество (теоретически бесконечное коли­чество) собственных частот. В режиме вынужденных колебаний при совпадении частоты возмущающей силы с собствен­ной частотой системы амплитуда колеба­ний резко возрастает. Это явление называ­ется резонансом.

Учет потерь. Характер вынужден­ных и свободных колебаний зависит от потерь в системе. Эти потери определяют­ся поглощением энергии в материале сис­темы, ее нагрузке, элементах крепления, излучением упругих волн в окружающую среду. Количественными характеристика­ми потерь служат коэффициент затухания, логарифмический декремент затухания и добротность [27, 123, 224, 300, 305, 312].

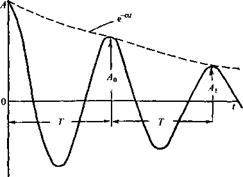
Коэффициент затухания колебаний а определяет закон убывания амплитуды А свободных колебаний во времени:

А =А0 e"<acos(co0t - cp),

где Ао - начальная амплитуда при t = 0; ©о - собственная круговая частота; ф - начальная фаза.

Промежуток времени т = 1/а, в тече­ние которого амплитуда уменьшается в е = 2,718 раза, называется временем релак­сации.

Логарифмическим декрементом за­тухания 0 именуют натуральный лога­рифм отношения соседних (отличающихся на период Го) амплитуд колебаний в мо­менты времени tnt + Т (рис. 1.66):

Величина 0 обратна числу периодов N, по истечении которых амплитуда колебаний уменьшается в е = 2,718 раза: 9 = 1 IN. Очевидно, что время релаксации

т = АТ0

Добротностью называют величину Q = 2пЕ0/Е„,

где Е0 - энергия, накопленная в системе; Еп - энергия, теряемая за один период.

Приведенное определение справед­ливо для любых значений Q. Добротность показывает, во сколько раз амплитуда вы­нужденных гармонических колебаний при резонансе превышает амплитуду при час­тоте, много меньшей резонансной, при одинаковой амплитуде возмущающей си­лы.

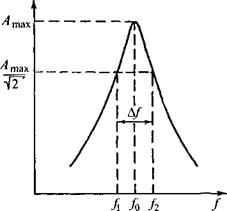
На практике добротность определяют как отношение собственной частоты f0 системы к ширине полосы Д/ частот, при которых энергия колебаний составляет не менее половины энергии при резонансе, а

амплитуда >Д= = 0,707 от амплитуды

V 2

колебаний при резонансе (рис. 1.67):

Эта формула справедлива при значе­ниях Q > (5 ... 10). При более низких зна­чениях добротности она дает несколько завышенные результаты.

Размерность коэффициента затуха­ния- с'1. Добротность Q и логарифмиче­ский декремент затухания 0 - безразмер­ные величины.

Рис. 1.66. Свободно затухающие колебания

Параметры, характеризующие потери в колебательной системе, связаны соот­ношениями

а = соо/2Є = 0/Го=і; (1.42)

Т

0 = ^ = аГо=^ = л/Є; (1.43)

Q = п /0 = п/аТ0 = со0 /2а = nN. (1.44)

В режиме вынужденных колебаний потери в системе находят путем измере­ния добротности по ширине полосы про­пускания. В режиме свободных колебаний потери определяют измерением логариф­мического декремента затухания. Послед-

Рис. 1.67. Частотная характеристика колебательной системы с затуханием

ний удобнее вычислять по изменению ам­плитуды за п периодов колебания по фор­муле

e=IinA.

п Ап

В отличие от пространственного ко­эффициента затухания 8, характеризую­щего потери при прохождении волной расстояния г (см. разд. 1.1.1), параметры а, 0, Q, т определяют процесс убывания амплитуды колебаний во времени.

Понятие добротности применимо не только к механическим или электриче­ским колебательным системам, но и к ма­териалам [242]. Добротность материала определяется через волновое число и ко­эффициент затухания: Qu = к/28 (здесь 8 - пространственный коэффициент зату­хания, рассмотренный в разд. 1.1.1). Зна­чение (2м можно определить эксперимен­тально, например как добротность сво­бодного стержня из данного материала. Если 8 прямо пропорционален частоте, что справедливо для многих металлов на невысоких частотах, то Qu не зависит от частоты. Значения добротностей для ряда

материалов даны ниже.

Алюминий............................... 10 000

Плавленый кварц...................... 5 000

Молибденовая сталь......... 4 700

Оконное стекло................... 910

Керамика.............................. 700... 5 000

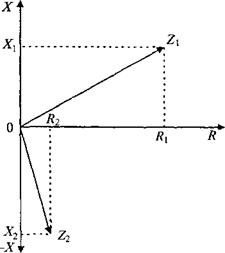
Механическим импедансом Z [203, 300, 312, 317] называют комплексное от­ношение гармонической (синусоидаль­ной) возмущающей силы F, действующей на поверхности (или в точке) механиче­ской системы к средней колебательной скорости v на этой поверхности (или в точке) в направлении силы: Z = F/v. Меха­нический импеданс является комплексной величиной и имеет активную R и реактив­ную X составляющие:

Z = R +jX = z е, ф, (1.45) где j = V-I; IZI = R2 +X2 - модуль импеданса; ф = arctg-^ - фазовый угол.

Активная (действительная) состав­ляющая R импеданса характеризует необ­ратимые потери. Последние обусловлены поглощением в материале системы, поте­рями энергии в нагрузке и элементах кре­пления, а также излучением упругих волн в окружающую среду.

Реактивная {мнимая) составляющая X импеданса характеризует кинетическую и потенциальную энергию, запасаемую и отдаваемую реактивными элементами системы. Реактивными элементами сис­темы являются инерционность и упру­гость. Инерционность связана с накопле­нием кинетической энергии движущейся массой, упругость - с потенциальной энергией упругого элемента (например, пружины). Активная составляющая им­педанса всегда положительна {R > 0), инерционная положительна (+Х), упругая отрицательна (—X) . Размерность механи­ческого импеданса - Н с/м.

Рнс.1.68. Графическое представление
механического импеданса на комплексной
плоскости

В некоторых источниках инерционную состав­ляющую считают отрицательной, упругую - положи­тельной.

Механический импеданс представ­ляют в виде вектора на комплексной плос­кости (рис. 1.68). По горизонтальной (дей­ствительной) оси отложена активная со­ставляющая, по вертикальной (мнимой) — реактивная. Символ j на мнимой оси опу­щен. Так, импеданс Z имеет инерционно­активный характер, импеданс Z2 - упруго­активный.

Во всех реальных системах сущест­вуют потери, поэтому всегда R Ф 0. Ино­гда, если R « ІХІ, влиянием R можно пре­небречь. Этим пользуются, например, при рассмотрении влияния механического импеданса нагрузки на собственные час­тоты системы, когда основное влияние оказывает именно реактивная составляю­щая импеданса.

В отличие от волнового сопротивле­ния z = рс, являющегося параметром сре­ды, механический импеданс Z - параметр конструкции и в отличие от рс не является удельной величиной. Значение Z опреде­ляется свойствами конструкции, в частно­сти для многослойной конструкции - все­ми параметрами ее слоев. При этом значе­ние механического импеданса конструк­ции зависит и от удельных волновых со­противлений материалов составляющих ее слоев.

Расчет механических импедансов возможен и целесообразен лишь для про­стых колебательных систем (стержней, пластин и т. п.). Некоторые их модели рас­смотрены ниже. В сложных случаях (на­пример, применительно к многослойным конструкциям, состоящим из различных материалов) более надежные результаты дает эксперимент.