При сварке нагрев изделия сменяется охлаждением, причем в общем случае для различных зон этот процесс сдвинут по

времени. То, что возмущающий фактор (температура) оказывает во времени непропорциональное воздействие на все зонн, вызы­вает сложное нагружение изделия (о простом я сложном нагру­жении см. 7.1.3). По этой причине для определения деформа­ций и напряжений в данный момент необходимо проследить всю историю деформирования изделия. Для этого весь рассматри­ваемый период разбивается на достаточно короткие этапы и на каждом из них находится решение с учетом решения на предыду­щем этапе.

Рассмотрим некоторый этап нагружения продолжительно­стью At. Изменение полных деформаций можно найти, проинте­грировав уравнения связи (7.22) на отрезке At :

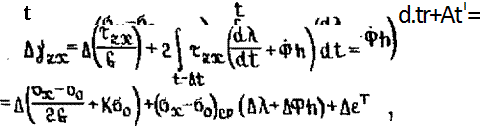И 7,23)

J

где (£x~OtP 1 ••• ) ('Чх'їср - некоторые значения компо­нент девиатора напряжения на интервале (t-At, t ), опреде-

ляемне теоремой о среднем интегрального исчисления. С по­грешностью аппроксимация 0(At) эти значения можно заме­

нить соответствующими значениями в момент t, которые будем

обозначать бх-б0 ,.,ггх в отличие от аналогичных величин

V”1LtX

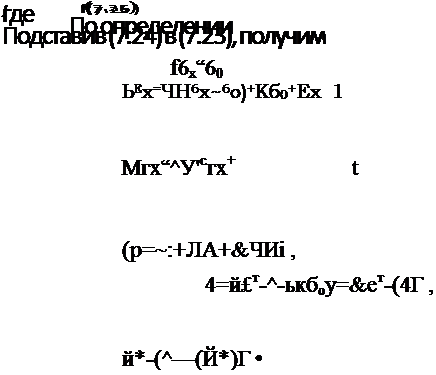(7.24)

Здесь функция <р определяет состояние материала, а £х,-Лгх “ начальные деформации (упругие деформации на пре­дыдущем этапе нагружения).

Подставляя выражение для б0 (7.2) в (.7.25), подучим уравнения, связнващие песть компонент приращения деформа­ции с компонентами напряжения:

£u) + K K-u> К-ф п

з"6*+~S+ ъ бг+£х I

НГ^б«+^ТпЧ + ,

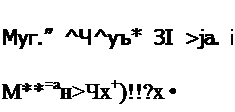О

Залижем уравнения С7.27) в матричной форме

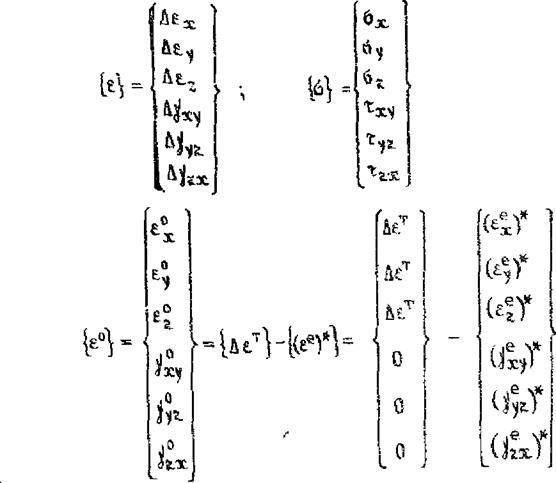М-В>ҐМ*И ,

Здесь [ВУ* - пластический эквивалент матриц податливости.

Решая уравнение (7.28) относительно напряжений, т. е. умножая его слева на матрацу [В] . обратную матрице [В] .

получим

и-мси-И) . (7-31)

где [В] - пластический эквивалент матрицы упругости, назы­

ваемый матрицей состояния:

Можно отметать, что при наличии только упругих деформа­ций ( ф-1/(г. с)) и начальных деформаций (е.0} в виде темпера­турных (є. т| as уравнения (7.31) получаются известные урав­нения теории упругости, связиващие шесть компонент напряже­ния о шесть® компонентами деформации за весь период нагру­жения:

Такам образом, для случая объемного напряженного состоя­ния получили уравнение связи между приращениями деформаций и напряжениями для некоторого произвольного этапа нагружения продолжительностью at в форме (7.31). Решение на текущем этапе нагружения зависит от начальных деформаций {е0} , а

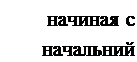они известны при последовательном прослеживали] момента t = О, когда их значения определяются

232

условиями.

Структура полученных формуя такая же, как и в теории упругости (ср., например, (7.8) и (7.29), (7.3Х) и (7.33). Отличие заключается в том, что имеются дополнительные дефор­мации {t° , а матрица [D] зависит не только от исходных

свойств материала Е и т) (формула (7.34)) , но и от текуще­го состояния материала (функция ^ ; см. формулу (7,32)), Следует отметить, что уравнение связи можно было по­строить относительно приращений деформаций и приращения на­пряжений, как это обычно делается в механике твердого дефор­мируемого тела. Однако тахой подход накладывает дополнитель­ное ограничение на вид кривой деформирования (такой подход не приемлем, например, для идеального упругопластического ма­териала) .