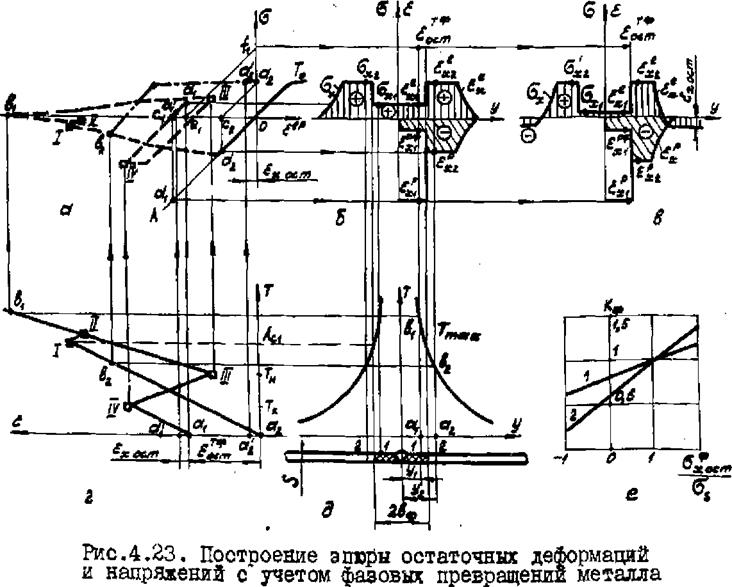
Для оценки объема продольного укорочения сварного со­единения с учетом базовых превращений металла выполним сле­дующее построение. Изобразим кривые максимальных температур по сечению пластины (рис.4.23,д), дилатометрическую кривую (рис Л.23,г) и диаграмму растяжения-сжатия (рис.4.23,а). На рисунке показана лишь одна ветвь кривой деформирования для исходной структуры металла. Для четкости рисунка остальные кривые деформирования (и для исходной структуры металла, и для стуктурн металла после превращений) опущены. Предполага­ется, что они имеют вид, изображенный на рис.4.21,а. Отме­тим, что масштаб шкал на диаграмме 6(tep) принят таким, что напряжения и соответствующие им упругие деформации характе­ризуются одинаковыми отрезками. Рассмотрим изменение дефор­маций и напряжений в призме I, расположенной в ЗФП ( у-Уі ), и в призме 2, расположенной вне этой зоны ( ^ = ). Прене­брегая полными деформациями по методу, изложенному в § 4.2, получим в первом приближении (рис.4.23,б) дилатацию, напря­жения, упругие и пластические деформации призм I и 2 в мо­мент максимального нагрева (отмечены соответственно Ь, и ) и после полного охлаждения (отмечены буквами сц и аа ). Видно, что в первом приближении конечное состояние призмы I характеризуется на плоскости 5(еер') точкой а, , а ее пол­ная деформация

с —+ — П

< ЬЭСI і Ь0СЛ1 1 и 1

где, - упругая составлящая полной деформации (деформа­ция удлинения); соответствует отрезку = а, “

пластическая составлящая полной деформации (деформация уко­рочения); соответствует отрезку OC^Cid^ ; 8otm» - составля­щая полной деформации, обусловленная фазовыми превращениями (деформация удлинения); соответствует отрезку ое1=о|, ,

ш

Конечное состояние призмы 2 характеризуется точкой аг, а ее полная деформация

где е^г - упругая составлящая полной деформации (деформа­ция удлинения); соответствует отрезку оса=оаг ; - пласти­

ческая составлящая полной деформации (деформация укороче­ния); соответствует отрезку осг=оаг.

Следует отметить, что построение эшзр остаточных напря­жений, упругих и пластических деформаций для призмы 2, как я для других призм, вне зоны структурных превращений не имеет особенностей и выполняется так же, как было описано в под­параграфах 4.4.4. Снося указанные отрезки на плоскость 5(у) и е.(у) (рис.4.23,б, слева и справа) и охватывая все призмы по сечению пластины, получим в первом приближении соответ­ственно эпюры остаточных напряжений, упругих (прямая штри­ховка) и суммарных пластических и фазовых (косая штри­ховка) деформаций. Определим последнюю из указанных эпюр

Ьф м

о Ьф

здесь Ьф - полуширина ЗФП,

С достаточной точностью можно принять в пределах

ЗФП одинаковыми. Тогда выражение (4.66) перепишем в виде

1 (4.67)

где $,х=~0,У55 - ia - эпюра остаточных пластических

деформаций при отсутствии фазовых превращений (см. 4.4.1). Ширина ЗФП в соответствии с (3.24) равна

(4.68)

на б3/Е

и

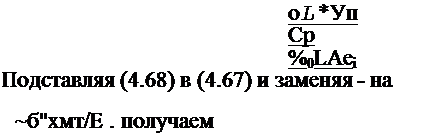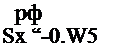<JL ^~gxocmN

Ср ъ V olEAtllna ] ’

Следовательно, объем продольного укорочения сварного

соединения с учетом фазових превращений

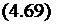рФ оФ J

-~01335^р

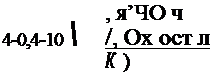где Кф - коэффициент, учитывакций влияние фазовых превраще­ний на объем продольного укорочения

(принято 72I°C, Е = 2*Ю5 Н/мм2, <э5 следует выра­

зить в Н/мн^).

На рис,4.23,е приведены графики изменения Кф, в зави - симости от «а /•» доя значений б^ = 250 я 500 Н/мм^,

Из рисунка видно, что фазовые превращения могут приводить я к увеличению и к уменьшению объема продольного укорочений сварного соединения. Если, то Кф> і ; и наобо­

рот, при б’хосш ^ учет фазовых превращений приводит к снижению ігхФ.

Вычислив по уравнению (4.S3), определяют значение

№

х С«р

и уточняют по формулам (4.63) или (4.65) остаточные напряже­ния в ЗФП. Эпюры распределения остаточных напряжений, упру­гих и структурно-пластических деформаций во втором приближе­нии показаны на рис.4.23,в. Видно, что в ЗФП упругие дефор­мации значительно уменьшились, в то время как деформации £^

не изменились; наоборот, в смежной зоне упругие деформации остались неизменными, равными е j?, а пластические деформации увеличились по абсолютной величине на! ехосш|.

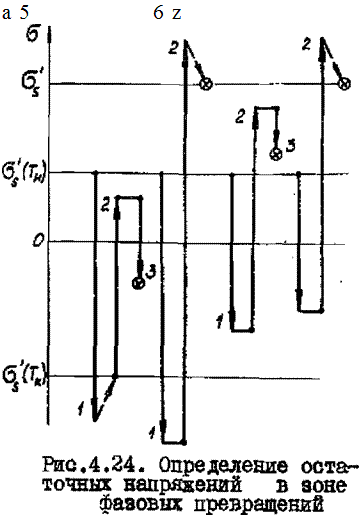
Проверку выполнения условий (4.61), (4.62) и (4.63) и соответствующее определение остаточных напряжений в 3® удобно производить графически. С этой целью по шкале (рис.4.24) в положительном направлении следует отметить зна­чения б^(Тн) и 6^ , ав отрицательном - бЦТк) . Затем, откладывая значения Ей£тф (отрезок Г, EJ, TK (отрезок 2),

Ф / V

Efcxocmtотрезок 3), как показано на рисунке стрелками.

можно непосредственно получить значения остаточных напряне - ний (обозначены кружком с крестиком).

Проиллюстрируем

Пример, ется определить с учетом фазовых превращений оста­точные напряжения и де­формации при однопроход­ной сварке встык двух по­лос размерами 150x10+ +50x10 на погонной энер­гии = 12600 Дж/см.

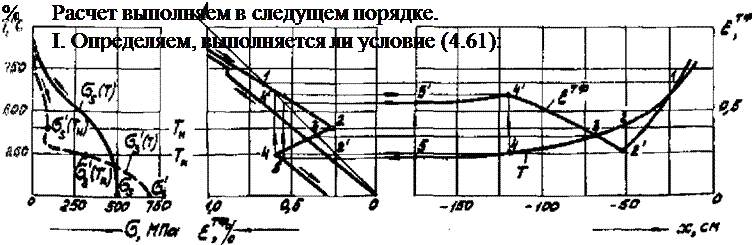
Анализ релаксомет - рической (рис.4.25,а) и дилатометрической (рис.4.25,в) кривых по­зволяет установить сле­дующие характеристики стали: Тн= 400°С, Тк = - 250°С, * 500 МПа,

ffi* 700 МПа, вг4(Тн^ = •* 120 МПа, ff;(TKV 325 МПа,

oL = I2.5-I0"6 I/°C, J? *

- X6-I0"6 I/°C, At1,41** 0,0035. Кроме того, принимаем

= 200 ГПа (изменением модуля упругости пренебрегаем) и ■ 4 Дх/смЗ.°С.

ЕЙ£ТФ=2Ч05 0,0035=?00 МПа, ®і(ти^+АЦтІ{>*іаО+За5='<А5МПа .

Следовательно, условие (4,61) выполняется, и в процессе распада аустенита происходит пластическая деформация укоро­чения.

2. Определяем, выполняется ли условие (4.62):

Ео1Тк=гч05чг,5 10“6-250 = бг5 МПа, 5^Тк>+^=Зг5+700= - ЮЄ5 МПа.

Условие (4.62) выполняется, следовательно конечный этап охлаждения протекает в упругой области, а эпюра остаточных напряжений имеет вид, соответствующий варианту I (см.

рис.4.22,а).

3. Вычисляем по (4.63) остаточные напряжения в ЗФП в первом приближении (принимая еХ(Кт = 0)

5il=EiTK'55W=^'^^0° МПа .

4. 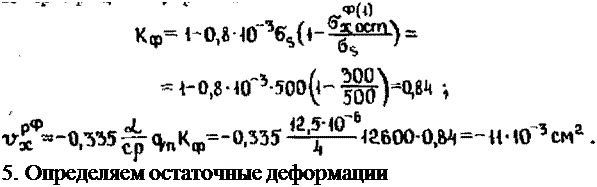Определяем по (4.69) объем продольного укорочения сварного соединения. Коэффициент, учитывающий влияние фазо­вых псевоашений. оавен

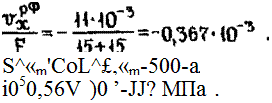хост

6. Уточняем по (4.63) остаточные напряжения в ЗФП

Приведенное решение получено при допущений одноосноети напряженного состояния. Вместе с тем это допущение при нали­чии фазовых превращений металла требует специального анали­за. Действительно, фазовые превращения обусловливают резкое изменение объема металла в относительно узком интервале тем­ператур ( ТН~ТК ). Поэтому они вызывают местное возмущение

4Л, погрешность одномерного решения зависит от гладкости объемных изменений металла вдоль оси шва. Чем больше интер­вал между Тн и и меньше сф, тем выше степень глад­

кости объемных изменений вдоль шва и тем меньше погрешность одномерного решения. Это видно из рис.4.25,в, на котором

изображены кривые изменения вдоль оси шва температуры (кри­вая 12345) и структурно-пластических деформаций (кривая 12'34'5!) для рассмотренного примера. Построение последней кривой выполнено путем отражения при помощи луча ОА

(рис.4.25,б) структурно-пластических деформаций на плоскость

ТФ

е.(х> . Для точек 4 и 5 указанное построение пояснено стрел­

ками: от кривой Т(х) проведены горизонтальные линии до ди­латометрической кривой (ветвь охлаждения), затем вертикаль­ные линии до луча О А и далее горизонтальные линии в обрат­ном направлении. до искомой кривой етф(х) . При уменьшении

температурного интервала между Тн и Тч и увеличении ьф проекция участка кривой 2-4 на ось х уменьшается, а на ось t увеличивается, что приводит к более резкому измене­нию характера кривой еТФ. В качестве оценочного критерия

применимости одноосного решения можно предложить соотношение

(4.71)

При невыполнении условия (4.71) допущение об одноосно - сти напряженного состояния не оправдывается. В этих случаях, так же как и при наплавке короткого валика (вне зависимости от вида дилатометрической кривой), требуется двуосное рас­смотрение задачи. Приближенные решения для указанных случаев излагаются в последующих параграфах.