Рассмотрение кинетики образования поперечных деформаций при наплавке валика на пластину (сварка встык двух ластов) выполним также при допущении одномерности напряженного со­стояния. Такой подход требует пояснения. Дело в том Р что одномерность напряженного состояния, как указывалось, оправ­дывается при одновременном наложении сварного шва по всей длине пластины и пренебрежении концевыми эффектами. Но в этом случае рассмотрение поперечных деформаций теряет инте­рес, так как они связаны непосредственно с продольными (ко­эффициентом Пуассона) и не соответствуют наблюдаемым в дей­ствительности. Поэтому схема одновременного наложения шва для определения поперечных деформаций является непригодной. Их рассмотрение требует учета особенностей температурного поля, возникающего в пластине от движущегося источника тепло­ты, т. е. учета неодновременное™ выполнения шва.

Итак, при рассмотрении продольных деформаций мы пред­полагали справедливой схему одновременного наложения шва, а при рассмотрении поперечных - от этой схемы вынуждены отка­заться и выдвинуть дополнительное предположение относительно характера перемещений точек пластины, используя, однако, при этом результаты определения продольных деформаций. Какое же дополнительное допущение о характере перемещений точек пластины при наплавке на нее валика можно выдвинуть? Для от­вета на этот вопрос вновь возвратимся к анализу упаутопла­

стических деформаций полоски шириною г! х, выделенной ' в

х) Такой искусственный и внешне противоречивый подход хаоак - тереп вообще для методов сопротивления материалов. В ка­честве примера можно указать, что при выводе формулы для нормальных напряжений пои изгибе балок предполагают чис­тый изгиб и получают известную формулу б=(М/1)?, используя

которую выводят формулу Журавского для касательных напря­жений, действующих в том же сечении (т=(Ы(1Ь)). Формальное

противоречие здесь заключается в том, что применяя закон плоских сечений в поперечном сечении балки, поедполагают, что касательных напряжений нет, а полученный при этом предположении результат используют для определения каса­тельных напряжении, признавая их существование.

пластине сечениями, перпендикулярними к шву (рис.4.17,в);

причем этот анализ разобьем на две части: сначала виявим физическую сущность процесса развития поперечних деформаций, т. е. ограничим анализ качественной стороной, а лишь затем произведем его приближенную количественную оценку.

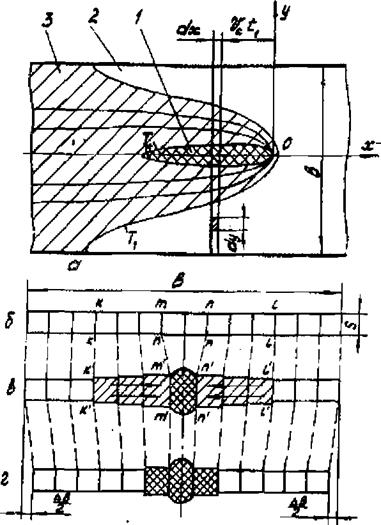Расчленим сечение по­лоски в исходном состоянии, т. е. до начала сварки, на одинаковые участки (рис.4.17,б) и проследим за изменением размеров этих участков вскоре после пересечения дугой рассмат­риваемой полоски (в момент t=t, ) и после полного остывания пластины. В мо­мент времени t| рассматри­ваемая полоска пересекает максимальную ширину изо­термы Т* (рис.4.17,а).

Будем различать в пластине три области:

1) нагретую вше Т*

(ограниченную изотермой Т* ), в пределах которой

металл находится в пласти - Рис.4.17. Образование по-

ческом состоянии разупроч - перечных сварочных дефор - . , „ мации

нения (на рис.4.17,а за­штрихована в клетку);

2) в пределах которой происходит постепенное понижение температуры от Тч до Т4 , незначительно отличающейся от начальной температуры пластины (косая штриховка);

3) в которой нет заметного повышения температуры (внеш­няя область по отношению к изотерме Т4 ); эта область охваты­вает нагретую область с трех сторон и создает для нее жест­кий подковообразный-контур.

В момент времени выделенная полоска пересекает все три области. Ее средние участки, принадлежащие области I и 2, вследствие теплового расширения стремятся увеличить свою ши­рину. Однако увеличение длины полоски исключено, так как ее

концевые участки принадлежат области 3 и жестко связаны меж­ду собой. Вместе с тем центральный участок полоски, принад­лежащий области I, находится в пластическом состоянии и прак­тически не оказывает сопротивления сжимающему усилию. По­этому стремление полоски удлиниться реализуется путем пере­мещения нагретых участков металла к ее середине. При этом концевые сечения полоски (слева от сечения к-к и справа от сечения 1-І ) не смещаются, а сечения нагретой зоны переме­щаются к центральной оси. В частности, сечения m-m и п-п ограничивапцие в полоске область I, перемещаются в положе­ние m'-m1 и п'—а* (рис.4.17,б, в). Происходит обжатие цент^- ральннх участков полоски на величину ЛЬ’ с образованием пластических деформаций укорочения в направлении оси у и увеличение их толщины (перераспределение объема металла в районе сварного соединения). Иначе говоря, участки, принад­лежащие области 2, увеличивают свою ширину ч одновременно уменьшается ширина участков, принадлежащих области X (при неизменной общей ширине пластины). Затем при охлаждении по­степенно восстанавливается исходная ширина участков, за ис­ключением средних, в которых возникли необратимые пластиче­ские деформации. В результате периферийные участки металла перемещаются к оси (рис.4.17,г), ибо область 3 при заверше­нии наплавки исчезает и ничто не препятствует уменьшению ши­рины пластины (предполагается, что наплавка ива выполняется по всей длине пластины). Таким образом, выполненный качест­венный анализ процесса позволяет сформулировать дополнитель­ное допущение* о характере перемещения точек пластины, а именно предположить, что увеличение ширины пластины (длины выделенной полоски) исключено, в то время как ее уменьшение протекает свободно.

Учитывая это дополнительное допущение, перейдем к при­ближенной количественной оценке поперечных деформаций. Рас­смотрим напряженно-деформированное состояние выделенной по­лоски в момент времени ti. При одномерном напряженном со­стоянии в соответствии с (2.7) поперечные деформации опреде­ляются по выражению

х) Основное допущение - одномерность напряженного состояния в зоне, расположенной за дугой, и сохранение плоских се­чений, ограничивающих выделенную полоску.

ІЗІ

£^=-0,5(-|г + е£)+оІТ, (4.34)

где - полная (действительная) деформация в направлении оси ^ .

Следовательно, произвольный участок выделенной полоски сЦ стремится изменить свои длину на величину e^dy, а вся

полоска - удлиниться на величину, Однако принимая

во внимание дополнительное допущение о неизменности длины по­лоски, мы можем утверждать, что в зоне разупрочнения (в об­ласти I) в результате ее обжатия возникнут пластические де­формации укорочения, суммарная величина которых ( ЛЬ1 ) должна быть равна недопущенному удлинению полоски с обратным знаком. Назовем указанные пластические деформации укороче­

ния в зоне разупрочнения деформациями обжатия, обозначим их

е.* и запишем сформулированное утверждение

Отсюда, принимая во внимание (4.34), имеем

AB'=0,5^4Y+0,5^t(MdrATft«Hl , (4,35)

В в в

где первый член правой части равен нулю в силу уравновешен­ности напряжении по сечению пластины; второй и третий представляют собой соответственно половину площади эпюры

продольных пластических деформаций и полную площадь эпюры

температурных деформаций в момент времени.

В § 4.3 было показано, что площади эпюр температурных и пластических деформаций в момент времени t, с достаточной точностью могут быть принятыми равными соответственно

1 . (4.36)

Подставляя (4.36) в выражение (4.35), получим ЬЪ’-оДо^Д^ За..

Таким образом, в момент времени суммарная величина поперечных деформаций обжатия определена, хотя не раскрыт за­кон их распределения. Для расчета поперечного укорочения

пяастины, как будет видно из дальнейшего, можно ограничиться полученным результатом. Однако для лучшего понимания физиче­ской сущности явления следует оценить величину поперечных деформаций обжатия. Принимая во внимание нормальный закон распределения температурных деформаций, естественно предпо­ложить, что поперечные деформации обжатия распределяются также по закону Гаусса:

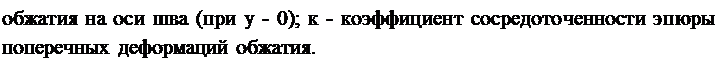
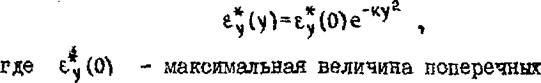(4.38)

Для определения указанных двух параметров тлеем два

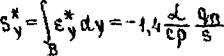УСЛОВИЯ;

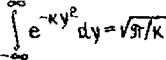Подставляя вместо е.^ его выражение из (4.38) я принимая во внимание, что

получаем

by (O’)*- М Щк (с£/(ср)|(j, n/s.

2. Область распространения поперечных деформаций обжа­тия ограничена ±ух . Полагая, что на указанных границах по­перечные деформации обжатия составляют Ъ% от их максимальной величины (на оси шва), можно записать

05^(0)

откуда

Подставляя (4.40) в выражение (4.39) и учитывая (3.24), окончательно получаем

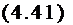t$tC0a~5,?ol. T# .

Отсюда видно, что максимальные поперечные деформации обжатия не зависят от мощности источника нагрева и при сварке мало­углеродистых сталей ( = 125 «ПГ6 1/°С; Т„.= 600°С) дости­гают « А% на оси шва.

Таким образом, распределение поперечных деформаций об­жатия (4.38) с учетом (4.40) и (4.41) можно переписать в ви­де

a*W—5.7J. T* . (4.42)

Дальнейшее развитие поперечных деформаций (при t>t< ) обусловлено изменением продольных деформаций и изменением температуры вследствие ее выравнивания и постепенного пони­жения из-за теплоотдачи с поверхности. При этом, как отме­чалось, происходит уже свободное (нестесненное) в поперечном направлении изменение размера произвольного участка полоски

Для иллюстрации выполненного анализа развития продоль­ных и поперечных деформаций проследим за изменением контура элемента dxdy, выделенного в области I (элемент I) и в об­ласти 2 (элемент 2). Для сокращения записи отнесем ребра элемента к их длине, т. е. будем рассматривать квадрат 1x1, и, следовательно, изменения размеров сторон квадрата равны соответствущим относительная деформациям.

На рис.4.18,а показаны составляющие продольных и попе­речных деформаций элемента I в момент. Тонкой сплошной линией обозначен контур элемента в исходном состоянии, штрих- пунктирной - при условии свободного теплового расширения, штриховой - при условии ограничения деформации в направлении оси х. и свободной деформации в направлении оси у, т. е. без дополнительного допущения, и жирной линией - действитель­ный контур в указанный момент времени (заштрихован). Так

к) При сварке .аистов больших габаритов, вследствие неодно - временнооти развития поперечных деформации на стадии осты­вания возникают поперечные растягивающие напряжения а листы испытывают плоское напряженное состояние.

р_ р *

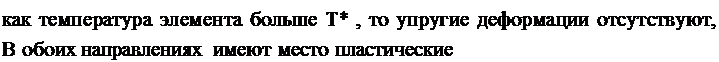
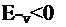
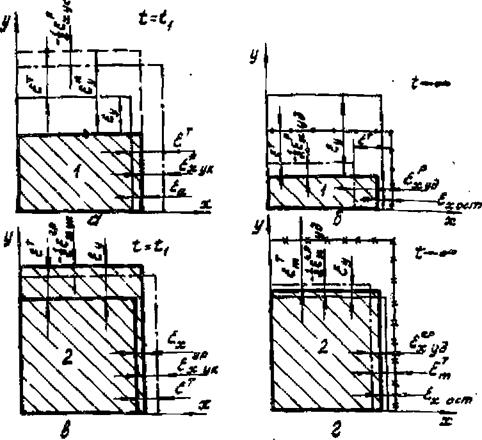V—), Е ТО ВРЄМЯ

как полные (дей­ствительные) де­формации - разных знаков ( &х> 0, Измене­ние контура эле­мента I после пол­ного остывания показано на

рис.4.18,б. Лини­ей с точками обозначен контур элемента в момент

t1 , штрихпунк - тирной - при ус­ловии свободного теплового сокраще­ния элемента, ' а жирной - его дей­ствительный контур t заштрихован), Здесь уже полные деформа­ции в обоих направлениях меньше нуля, причем по абсолютной величине £n»ex. Аналогично на рис.4,18,в, г показано из­менение контура элемента 2, в момент t< и после полного остывания, в отличие от элемента X, в элементе 2 не возника­ет поперечных деформаций обжатия а5 и процесс развития в

нем упругопластических деформаций не имеет особенностей (по­перечные деформации обусловлены продольннми и нагревом). Сле­дует лишь отметить, что для определения контура элемента по­сле полного остывания (и вообще на стадии остывания) необ­ходимо иметь данные о контуре элемента в момент его макси­мального нагрева (изображен линией с крестиками).

Поперечные деформации обжатия е* можно рассматривать

как дополнительные (начальные) пластические деформации. По­этому поперечная деформация произвольного элемента &у при t>t< может быть определена по уравнению (2.3) с дополни­тельным членом Е* , Т. е.

ty=-Q,5^jp-+S:.£.}+£T+£^ і (4.43)

соответственно изменяется длина выделенной полоски, т. е. ширина пластины

bB(t)= ^cbj=-0,-0фdy +|iTdy+£*dy. (4.44)

В В В в в

Первый член правой части уравнения (4."44) равен нулю, так как напряжения бх по сечению уравновешены. Второй

член - в соответствии с (4.13)

. (4.45)

Третий член выражения (4.44) характеризует изменение длины полоски вследствие нагрева и с учетом (4,11)

, (4.46)

Последний член выражения U.44) бш определен выше (4.37).

Подставляя в уравнение (4.44) выражения для его слага­емых (4.45М4.37), окончательно получим

AB(t)=^^[p(ty^v(t)] , (4.47)

где

^у(^ = -[М+0,5^х(1;)] . (л.48)

Функцию jiy(t) будем называть функцией поперечных

пластических деформаций, а ее конечное значение (при t~«>)- коэффициентом поперечного укорочения сварного соединения

( jul у ). Обычно время сварки незначительно но сравнению с по - следущим периодом остывания. Поэтому изменение функций p(t) и jT^(t) по длине пластины также незначительно и ее ширина постепенно уменьшается почти равномерно по всей длине.

Следовательно, полоска шириною dx при t>ti беспре­пятственно изменяет свою длину, а значит, и объем в направ­лении оси у :

dtr^=A5sdx=ф tyndx [p(t)+jLy (t)]

136

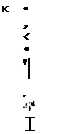или, относя к единице длины:

Поэтому поперечное укорочение пояска таврового соединения обусловливается не всей погонной энергией нагрева, а только той ее частью, которая вводится в рассматриваемый элемент (поясок),

Сравнивая формулы (4.19) и (4.50), определяющие объемы продольного и поперечного укорочения сварного соединения, легко обнаружить их сходство. Действительно, объемы про­дольного и поперечного укорочения сварного соединения про­порциональны погонной энергии нагрева и обобщенному пара­метру д,/(ср) , характеризующему способность металла изменять

объем при нагреве. Однако коэффициенты jпх и ^ , как пра­вило, существенно отличны один от другого.