Уравнение теплопроводности выводится на основе за­кона теплопроводности Фурье. Вблизи произвольной точки А тела (рис. 55) выделим бесконечно малый объем в виде параллелепипеда со сторонами dx, dy, dz. Через грани в эт9Т обьем поступает тепло от более нагретых участков тела и од­новременно он сам отдает тепло менее I

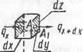нагретым участкам. Если объем от­дает тепла меньше, чем получает, то избыток расходуется на его нагрева­ние. Подвод тепла к выделенному объему и его отдача могут происхо­дить через любые грани в направле­ниях X, К, Z. Поэтому необходимо рассмотреть тепловые потоки и теп - / ~ г /

ловой баланс по всем трем коорди - / /У

натным направлениям. ХА-___ х-___ А

Если по ребру АА, температура изменяется в зависимости от х, т. е.

Т —Т (х), то в общем случае градиен­ты температур в точках А и Ах раз­личны, а следовательно, и удельные потоки тепла, притекающе­го к грани х и оттекающего от грани x + dx, будут различны.

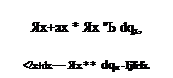Приняв, что удельный тепловой поток на грани х равен qx, а аналогичный поток на грани х - f dx равен qx+(jx, представим, что Ях+dx равен q, плюс приращение потока или его уменьшение на пути dx. Тогда можно записать, что

Так как количества йритекающего и отходящего тепла не равны между собой, то в выделенном элементе dx dy dz будет, например, накапливаться тепло dQx, величина которого может быть найдена как разность всего подведенного и отведенного тепла в направле­нии оси X за время dt:

dQx — qxdy dzdt — qx+dx dydzdt = —dqx dy dz dt =

= — ^ dx dy dz dt.

Аналогично рассуждая в отношении тепловых потоков по коор­динатным направлениям Уи Z, выведем выражения для dQy и dQz.

dQy —---- ^ dy dx dz dt;

dQz — — — dz dxdy dt.

Поскольку общее накопление тепла в объеме dxdydz равно сумме накоплений по всем трем направлениям, то

dQ = - dx dydzdtfy + %+%). (IV.13)

Подставляя в выражение (IV. 13) значения qx, qy, qz, получен­ные из уравнения (IV.6):

, дТ. , й1, , дТ

Ях — КХ дх > Яу~ КУ ду, Яг~ ' г Qx »

будем иметь

dQ = —dx dy dz dt [I {-K§) + |(-X, I) +

Если принять, что рассматриваемое тело изотропно, т. е. имеет оди­наковую теплопроводность по всем направлениям, а также, что тепло­проводность, теплоемкость и плотность не зависят от Т, то можно считать — К = I п вывести к за знак дифференциала. Тогда

уравнение (IV.14) примет вид

dQ = x{S+W + S)dxdy dz dL (IV-15>

Это количестве тепла повысит температуру элементарного объема

ОТ

dxdydz на величину dT = dt, в связи с чем его можно выра­

зить как произведение объема, теплоемкости и приращения темпе­ратуры:

v * — • ^ АТ*

dQ"*dxdyd2i^-j^dt. (IV. 16)

Приравнивая правые части равенств (IV. 15) и (IV. 16), а также сокращая на dx dy dz dt, получим

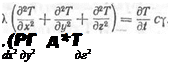(IV. 17)

Дифференциальное выражение

называют оператором Лапласа. Оно представляет собой - сумму вторых частных производных от функции температуры Т = — Т (х, у, z, t) по осям X, Y, Z. Для упрощения записывают это вы­ражение в виде

&Т д2Т , &т _ ът дх2 + ду2 + дг2 ~ V 1 •

Тогда

f = или f =ау2Т. (IV. 18)

Отношение теплопроводности К к объемной теплоемкости су на­зывают коэффициентом температуропроводности а, см2!сек. Он ха­рактеризует скорость выравнивания температуры.

В дальнейшем будем принимать коэффициент а не зависящим от температуры. В действительности он зависит от нее довольно сильно, но учет этого фактора усложняет соотношения (IV. 16) — (IV. 18), приводя к нелинейным дифференциальным уравнениям.

Частные случаи уравнения теплопроводности. Уравнение тепло­проводности (IV. 18) выведено для общего случая распространения тепла. Для некоторых способов сварки общее уравнение теплопро­водности можно значительно упростить. Рассмотрим примеры та­кого упрощения:

I. В тонкой пластине температурное поле можно отнести к плос­кой системе координат, так как температура равномерно распре­делена по толщине пластины и не зависит от координаты г, т. е.

~ ~ 0. Тогда уравнение теплопроводности приобретает вид

(IV. 18а)

2.

В длинном тонком стержне, трубе и других подобных дета­лях температура может быть распределена по поперечному сечению равномерно и не зависеть от у и г, т. е.

3. В условиях теплового равновесия при длительном устано­вившемся процессе каждый элемент получает тепла столько же, сколько отдает. В этом случае температура любого элемента тела

дТ

постоянна: Т = const, (jt = 0, Тогда уравнение теплопроводности приобретает вид уравнения Лапласа:

сРТ л.^1

дх2 + дуг + дг2 ~

4.

Уравнение плоского стационарного процесса будет иметь вид

5. Уравнение линейного стационарного процесса, зависящего лишь от координаты х,

S = №8д)

В последнем случае температура не зависит ни от каких других переменных, кроме х, поэтому частную производную можно заменить ролнрй:

а?-о - (1УЛ8е)

Краевые условия. Для расчета процесса распространения тепла недостаточно одного уравнения теплопроводности. Должны />ыть заданы еще и краевые условия: начальное распределение темпера­тур по трлу и условия обмена тепла на границах рассматриваемого тела.

Условия теплообмена на границах тела могут быть весьма раз­нообразны. Для практического использования особенно важны три из них:

1. Изотермическое условие. Полагаем, что поверх­ность тела обладает постоянной температурой в течение всего про­цесса распространения тепла. Такое состояние возможно, например, при сварке с интенсивным омыванием изделия водой.

2 .Адиабатическое условие. Теплообмен на гра­ницах тела считаем равным нулю. Практическим примером этого условия может служить сварка при наличии тепловой изоляции поверхности детали асбестом, сухим песком и т. п.

3. Условия теплообмена на границе со средой заданной температуры. В этом случае тепловой поток на границе пропорционален разности температур изделия и среды:

9S = (Ts - Т0) а., где Т0 — температура среды;

Ts — температура рассматриваемой точки поверхности тела.

В то же время к границе притекает тепло в соответствии с за коном теплопроводности:

Если теплоотдача очень велика, а приток тепла мал 00]■

температура поверхности тела приближается к температуре окру­жающей среды, т. е. условия теплообмена близки к изотермическим.

Если отдача тепла незначительна, а приток его интенсивен ^ -> oj>

то теплообмен на границе убывает и в конечном счете станет равным нулю, т. е. получим адиабатические условия обмена.

Нетрудно видеть, что третье условие является более общим, т. е. включает в себя как предельные изотермический и адиабатический случаи теплообмена на границе.