Идея расчета ТЦП сложного изделия заключается в условной замене его моделью «массивного» сплошного тела с простой фор­мой поверхности (цилиндр, пластина или шар), материал которого обладает той же теплопроводностью, что и материал изделия, а тепловые свойства эквивалентного массивного тела выражены в виде эквивалентных коэффициентов [81]. В этом случае расчет­ное время, нагрева и охлаждения массивного тела будет совпадать с временем нагрева и охлаждения паяемого изделия с достаточ­ной для практики точностью.

В ряде случаев также важно знать распределение температу­ры по объему паяемого изделия и изменение температурного поля при пайке. Для решения этой задачи используют известные методики расчета, учитывающие особенности конструкции паяемо­го изделия, его форму и конечные размеры.

Для расчета термических циклов при пайке с локальным источником нагрева, например газопламенным или электрической дугой, может быть использована теория движущихся сосредоточен­ных источников тепла с учетом влияния размеров и формы изделия, разработанная применительно к сварке академиком Н. Н. Рыкалниым.

Существует общий подход к расчету термического цикла пайки изделий, при общем нагреве не зависящий от вида тепло­обмена и конструкции паяемого изделия. Если известен способ нагрева при пайке, конструкция паяемого изделия, температура и давление при пайке, то можно определить вид теплообмена между паяемым изделием и окружающей средой и условия одно­значности теплообмена.

Условия однозначности включают физические параметры ма­териала конструкции и окружающей с'реды (физические условия); геометрическую форму и габариты изделия (геометрические усло­вия); температурное поле в начале нагрева или охлаждения (начальные условия); закон теплообмена на границе паяемого изделия с окружающей средой (граничные условия).

Закон теплообмена на границе паяемого изделия с окружаю­щей средой может быть задай в виде известной температуры на поверхности паяемого изделия на протяжении общего времени пай­ки (граничное условие 1-го рода). Граничное условие 2-го рода определяет значение теплового потока, поглощаемого (выделяемо­го) изделием за общее время пайки. Граничное условие' 3-го рода определяет температуру окружающей среды и закон Теплообмена на поверхности паяемого изделия: а(Т0.с—Гп) —^~-%пдТ? дп, где а — коэффициент теплопередачи, ВТ/м2-К); ?.п—коэффициент теплопро­водности паяемого материала, Вт/(м2-К); Го. с—.температура окру­жающей среды, К; Тп — температура поверхности паяеАюго изде­лия, К; д'Т/дп — градиент температуры,! К/м.' ; . і.' і Г

Граничное условие третьего, рода,, является, математической за­писью закона сохранения энергии. ;J,

Граничное. условие. 4-го рода описывает, кондуктдвньда ; тепло­обмен между поверхностью паяемого гізделйяір. окружающей .сре­дой, когда температура поверхности паяемого изделия равна тем­пературе окружающей среды. Это условие математически, формули­руется в виде равенства тепловых, потоков от окружающей среды к паяемому изделию и обратного:

— К-с (dT0.Jdn) = —(дТпідп).

Выбор модели паяемого изделия в виде массивного сплошного тела простой геометрической формы основывается на близости форм поверхностей паяемого изделия и тела. Если паяемое изделие пред­ставляет собой тело вращеииея, то.. выбирают цилиндр; или шар. Для цилиндра определяющий размер: рассчитывается по формуле:

Ц. г= F/к, Для пластйиы l=F/2&, для itiapa ft '==‘f3V^/4'it,

где F — площадь поперечного. сечения пластины или цилиндра, м2; 6— половина толщины пластиды, м; У-г:р(5ъем/щара, м3, г, і Дальнейший ход расчета определяется, видом теплообмена. меж­ду паяемым изделием и окружающей средой.

, Условия однозначности, определяющие размер изделия и вид теплообмена, позволяют рассчитать критерий, массивности Био паяе­мого изделия: Bi=allK, где а — коэффициент теплооїдачщ В'т/(й2;

•К); Я — Коэффициент теплопроводности паяемого материала, Вт/‘ /(м-К); I — размер паяемого изделия, м.

Если в процессе иагрева (охлаждения) можно пренебречь гра* диентом температуры в объеме паяемого изделия (Ві<0,25), то - последнее считается теплотехнически «тонким»; если градиент тем­пературы значителен (Ві>.0,5), то изделие считается теплотехни­чески «толстым».

Расчет времени нагрева и охлаждения тел

при кондуктивном теплообмене (теплопроводность)

где а — температуропроводность, мг/с.

Граничное условие задано в виде известного закона теплооб­мена и температуры окружающей среды.

Решение уравнения (1) определяет температуру тела как функ­цию трех координат и времени: t=f(x, у, г, т).

Рассмотрим случаи двустороннего нагрева бесконечной пластины; толщиной 26. Бесконечной считается пластина, у которой толщина - значительно меньше ее ширины и длины. В этом случае коэффи­циент теплоотдачи неизменен по всей поверхности пластины; следо­вательно, изменение температуры происходит вдоль одной оси. Общее решение уравнения (1) (в безразмерной форме) для; пластины можно записать в виде

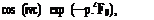
2 sin рп

"і Рп + sin Рп COS Pn

где 0 — температура; х — координата; Fo — критерий Фурье; р — постоянная, определяемая значениями критерия Био [82].

Безразмерная температура 0=(7’о. с—Т)/(Т0.с—Т0), где Г —тем­пература тела в данный момент времени, К; То— начальная темпе­ратура тела, К.

Значение р критерия Фурье рассчитывается по формуле Г0=» —ах/Р, где t—время нагрева (охлаждения); I — размер изделий, м.

. Ряд (2) быстро сходится, причем для критерия Фурье Fo»0,2S> величина относительной температуры определяется с достаточной1 точностью первым членом ряда («—1):

В = 2 sln. fo----- cos р* exp ( - p2F0) •

Ki+ sin Pi cos Pi

Величина относительной температуры для заданного сечения пластины определяется значениями критериев Фурье и Био. Это условие позволяет графически решить уравнение (2). Для поверх­ности н середины пластины графическое решение представлено иа рнс. 35. Этн графики позволяют оценить максимальный темпера­турный перепад по сечеиню пластины при нагреве (охлаждении) паяемого изделия. Аналогичные графики построены и рассчитаны для цилиндра н шара.

Для определения температурного поля по объему паяемого изделия выбирают координату точки в объеме паяемого изделия, задают максимальный возможный граднеит температуры (gradr»

—То. с—Т), исходя из теплофизических параметров паяемого мате­риала и конструкционных особенностей изделия, определяют по - заданному градиенту величину относительной температуры, опре­деляют по таблице значение коэффициента X, подставляют полу­ченные значення х, 0 в уравнение (1) или (2) и рассчитывают время нагрева (охлаждения) паяемого изделия до заданной температуры в точке, выбранной в его объеме.

Выбирая последовательно координаты точек от поверхности к. центру, можно получить изменения во времени температурного поля по объему паяемого изделия.