Научные теории можно разделить на две группы: феноменологические и

детерминистические. Феноменологические теории - это теории описательного плана, когда незнание причины явления возмещается аппроксимацией экспериментальной зависимости математической формулой. Это довольно мучительное направление исследований, поскольку поиск математической формулы зачастую бывает чрезмерно трудоемким и требует разработки довольно сложного математического аппарата. Идеальная теория - это детерминистическая теория, когда известны причины явления и физическая модель процесса, позволяющая получить аналитический вывод математической формулы для описания самого явления. Но это еще более трудная задача, поскольку необходимо найти
правильно физическую модель. На рис. 10, 11, 12 представлены модели формирования гравитационного поля в результате сферической деформации квантованного пространства - времени, математическое описание которых уже не вызывает никаких трудностей. Но представленные выше модели являются статическими и не учитывают скорость движения частицы (тела) в квантованном пространстве-времени.

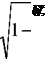Экспериментально было установлено, что с увеличением скорости v частицы ее масса m возрастает, и особенно резко в области релятивистских скоростей, близких к скорости света С

где у - релятивистский фактор.

Выражение (68) отличается от широко известного тем, что масса mo привязана к неподвижному абсолютному квантованному пространству-времени с гравитационным потенциалом C2, определяя энергию (56) покоя частицы. Но выражение (68) имеет

недостаток в том, что при увеличении скорости v частицы до скорости света С0 масса частицы увеличивается до бесконечности. Это можно было принять за истину, если бы само квантованное пространство-время не характеризовалось предельными параметрами, в том числе конечной величиной скорости света Со, которая не безгранична. Это означает, что релятивистские частицы, даже при достижении на скорости света, должны обладать предельными конечными, но не бесконечными параметрами. Чтобы решить поставленную задачу, заменим релятивистский фактор у в (68) введением в баланс (64) нормализованного релятивистского фактора yn, ограничивающего предельные параметры релятивистской частицы коэффициентом kn нормализации, приравняв баланс (64) к нулю при v=Co

v

n C2 Co

Подставляя в (69) фп (60) при r=RS и v=Co, находим величину коэффициента kn нормализации и значение нормализованного релятивистского фактора yn [12-17]

1

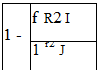Y n = , . ..= (70)

v

Co

Теперь можно записать динамический баланс гравитационных потенциалов частицы во внешней области квантованного пространства-времени, характеризуя ее состояние во всем диапазоне скоростей, включая скорость света Со, и определяя предельные параметры массы mmax и энергии Wmax при достижении скорости света v=Co [12-17]

Выражения (69)...(73) получены при условии, что в предельном случае при достижении скорости света, релятивистская частица переходит в динамическую черную микродыру с радиусом RS. Протон при достижении скорости света в соответствии с (72) и

Rs=0,8'10~15 м приобретает предельную массу порядка 1012 кг, соответствующую массе железного астероида диаметром 1 км.

Умножая (71) на RS/G при r= RS получаем баланс динамической массы m частицы во всем диапазоне скоростей в абсолютном квантованном пространстве-времени

m = Ynmo = mmax - ms (74)

В (74) входит скрытая масса ms частицы, как мнимая компонента квантованного пространства-времени. В результате динамическая масса m (74) частицы определяется разностью ее предельной mmax и скрытой ms масс. При увеличении скорости частицы увеличение динамической массы частицы происходит за счет уменьшения ее мнимой компоненты, обеспечивая баланс (74). Физически это происходит в результате того, что знакопеременная оболочка нуклона как полевая сетка захватывает во внутрь все большее количество квантонов, увеличивая квантовую плотность среды внутри квантона за счет снижения ее с внешней стороны, как это показана на гравитационных диаграммах рис. 11 и 12. Это ведет к увеличению сферической деформации среды, и соответственно, к увеличению массы частицы.

Умножая баланс массы (74) на C2 получаем динамический баланс энергии частицы во всем диапазоне скоростей, включая скорость света

W = YnWo = Wmax - Ws (75)

В (75) входит скрытая энергия Ws частицы, как мнимая компонента квантованного пространства-времени. В результате динамическая масса W (74) частицы определяется разностью ее предельной Wmax и скрытой Ws энергий. При увеличении скорости частицы увеличение динамической энергии частицы происходит за счет уменьшения ее мнимой компоненты, обеспечивая баланс (75).

В области малых скоростей v<<Co нормализованный релятивистский фактор yn (70) переходит в фактор у (68), который можно разложить в ряд, и, отбрасывая члены высших порядков привести баланс (75) к известному виду

Как видно из (76) увеличение кинетической энергии частицы с увеличением ее скорости равносильно увеличению ее динамической массы m=W/ C2.

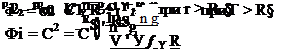В общем случае состояние динамической частицы в квантованном пространстве- времени описывается распределение квантовой плотности среды (42) и гравитационных потенциалов (57) введением нормализованного релятивистского фактора yn (70), учитывающего абсолютную скорость v частицы

Динамические системы (77) и (78) являются решением динамического уравнения Пуассона для распределения квантовой плотности среды р и гравитационных потенциалов ф, которые удобнее записать в векторной форме:

C2

-°divgrad(p0 ± уnрn) = 4nGpm (79)

Р o

divgrad(Co ± ynФn) = 4nGpm (80)

где pn - квантовая плотность среды, обусловленная ньютоновским потенциалом фп (66),

квантон/м3.

В уравнения Пуассона (79) и (80) под операцию divgrad введены постоянные интегрирования р0 и C2, которые могут быть выведены из-под операции дифференцирования как в (50) и (63), поскольку производная от константы равна нулю. Но в этом случае теряется физический смысл двухкомпонентных уравнений (79) и (80), поскольку их решения определяются системами (77) и (78) для внешней и внутренней областей сферически деформированного пространства-времени. Знак (-) в (79) и (80) соответствует внешней области, а знак (+) - внутренней области. При этом параметр рт в (79) и (80) выступает как плотность вещества в [кг/м3], рожденного в результате сферической деформации квантованного пространства-времени, которая возрастает с увеличением скорости частицы. Причем уравнения (79) и (80) являются эквивалентными, но записанными через разные параметры (66) квантованной среды.

Как уже отмечалось, еще никому не удавалось, не только найти точные решения, но и составить корректное динамическое гравитационное уравнение Пуассона, описывающее состояние частицы в квантованном пространстве-времени во всем диапазоне скоростей, включая релятивистские. Это удалось сделать благодаря квантовым представлениям на природу гравитации, когда квант пространства-времени (квантон), как универсальная объединяющая частица, является носителем гравитационных взаимодействий. Открытие квантона послужило основой квантовой теории гравитации (КТГ).

Несомненно, что классическое уравнение Пуассона (50) уже давно не удовлетворяло теорию гравитации, и попытки найти ему подходящую замену предпринял Эйнштейн в общей теории относительности (ОТО), представив его в тензорной форме [38]:

Rik -2gikR = - XTik (81)

Сравнивая уравнение (81) с новыми уравнениями Пуассона (79) и (80), можно увидеть, что новые уравнения значительно проще, и имеют однозначные решения (77) и (78). В то время, когда Эйнштейн работал над теорией гравитации в рамках ОТО, такие параметры квантованного пространства-времени как квантовая плотность среды ро, р1, pn, р2

(66) была неизвестна, а из соответствующих (66) четырех гравитационных потенциалов C2,

С2, фп, ф2, был известен только один ньютоновский потенциал фп. Естественно, что, не зная истинных параметров квантованного пространства-времени, описать гравитационное состояние частицы (тела) или нескольких частиц (задача многих тел) не представлялось возможным. Поскольку уравнения (79) и (80) с введением нормализованного релятивистского фактора yn являются нелинейными, и их точное решение найти чисто математическими методами для пространства с произвольной кривизной, не представляется возможным. Однако решения находятся значительно проще, учитывая физическую модель сферической деформации квантованного пространства-времени, когда динамическая кривизна kRV пространства-времени задана простыми параметрами в (77).. .(80)

Y nRg

r

Решения (77) и (78) описывают состояние одной частицы в квантованном пространстве-времени при отсутствии внешнего гравитационного возмущения. При наличии нескольких источников гравитации, необходимо составить системы уравнений (77) и (78), оперируя к их внешней области и последовательно устанавливая иерархию воздействия от более сильного источника к более слабому. Это определяется тем, что слабый источник гравитации находится внутри гравитационной ямы более сильного источника, а не наоборот. Только так можно сформулировать постановку задачи многих тел, когда гравитационное поле в динамике представляет собой сложную нелинейную функцию с нелинейной кривизной. Но, учитывая принцип сферической инвариантности, решение такой сложной задачи может быть сведено к суперпозиции полей, как сферических полей точечных источников с радиусом Rg, что значительно упрощает решения. Так, например, вращение орбитального электрона в гравитационной яме протонного ядра по сильно вытянутой орбите не позволяет электрону излучать, поскольку увеличение электрической энергии при приближении электрона к ядру компенсируется эквивалентным уменьшением гравитационной энергии системы, которая ранее никогда не учитывалась в расчетах [11]. Квантовые проблемы излучения орбитального электрона решает квантовая теория гравитации (КТГ).

Понимая нелинейный характер гравитации, Эйнштейн вынужден был искать уравнения, которые, по его мнению, должны были бы более полно подходить для описания гравитации, в том числе в области релятивистских скоростей. Для этого классическое уравнение Пуассона необходимо было модернизировать в (81), заменив divgrad(9) на Rik. В правую часть взамен 4nGpm введен тензор xTik. Член ^gikR добавлен из формальных соображений [38]. Кривизну пространства в (81) характеризует тензор Риччи Rik взятый из аппарата римановой (неэвклидовой) геометрии, добавив в (81) тензор Tik энергии импульса материи. Несомненно, решения тензорного уравнения (81) не столь простые как системы из (77) и (78). Уравнения Пуассона (79) и (80) также можно модернизировать и свести к одному уравнению, выразив гравитационные взаимодействия безразмерной динамической кривизной kRV (82) пространства-времени

1- , , ч 4nG

divgrad(1 ± kRV) = —— р m (83)

С 2

Уравнение Пуассона (83) интересно тем, что оно напоминает уравнение Эйнштейна (81) тем, что не оперирует классическими параметрами гравитационного поля, а только его кривизной, как относительным безразмерным параметром.

Все уравнения (69)... (84) получены при условии сферической деформации квантованного пространства-времени, определяя принцип сферической инвариантности во всем диапазоне скоростей, включая релятивистские. Это означает, что гравитационного поле элементарной частиц остается сферическим с увеличением ее скорости до скорости света, когда она переходит в динамическую релятивистскую черную микродыру, сохраняя сферическую форму. Как отмечалось, действие принципа суперпозиции полей позволяет перенести принцип сферической инвариантности и на космологические объекты, включая планеты. Если бы гравитационное поле Земли сжималось в направлении движения, то это обнаружилось бы в опытах Майкельсона и Морли [20]. Но это не было зарегистрировано. По сути дела, опыты Майкельсона и Морли дают экспериментальное подтверждение принципу сферической инвариантности.

Ранее была получена формула (65) скорости света в статическом гравитационном поле. Теперь, оперируя к динамическому балансу (71) гравитационных потенциалов во внешней области квантованного пространства времени определяем скорость света С в любой возмущенной гравитацией области с динамическим потенциалом упфп во всем диапазоне скоростей, включая релятивистские

Выражение (84) показывает, что скорость света на поверхности земли в горизонтальной плоскости ввиду сферической симметрии гравитационного поля Земли остается величиной постоянной для данной скорости. Это означает, что плечи интерферометра Майкельсона должны зафиксировать одинаковую скорость света в направлении движения Земли и поперек движения, подтверждая принцип сферической инвариантности. Земля ведет себя как независимый центр в квантованном пространстве - времени, сохраняя свое сферическое гравитационное поле в локальной области пространства.