ЗАКОН ВИДЕМАНА-ФРАНЦА-ЛОРЕНЦА
 23 марта, 2016
23 марта, 2016  Mihail Maikl
Mihail Maikl ![]() В XIX в. физики сталкивались с большими трудностями при экс-
В XIX в. физики сталкивались с большими трудностями при экс-
-гриментальном определении теплопроводности материалов. В середине XIX в. «Спериментально было показано, что, по крайней мере, для металлов отношение 'к/о является постоянной величиной. Таким образом, зная это отношение, полно определить теплопроводность любого металла, измерив его электрическое сопротивление, что довольно просто. Закон, устанавливающий зависимость между теплопроводностью, электропроводностью и абсолютной температурой, получил ■азвание закона Видемана-Франца-Лоренца, и его справедливость в принципе может быть доказана на основе классической модели электропроводности.
Рассмотрим теплопроводность одномерного газа, в котором имеется продольный температурный градиент (рис. 5.11). Поверхность А, находящаяся в нача - координат, перпендикулярна направлению движения молекул. Примем, что сум.Йфный поток массы через эту поверхность равен нулю. Тогда
![]() nlvl + n2v2 = 0.
nlvl + n2v2 = 0.
В дальнейшем мы будем использовать символ / для обозначения длины свободного пробега, а не длины образца, как это было раньше. Молекулы, дви - шиеся слева и пересекающие поверхность А, приходят в среднем из точки координатой -1/2. 2
Рис. 5.11 Теплопроводность в одномерном газе
Пусть их кинетическая энергия равна U ( //2). Тогда молекулы, пересекающие верхность А справа, имеют кинетическую энергию Половина молекул
ижется налево, а другая половина направо. Суммарный энергетический поток,
Энергия каждой молекулы равна (1/2) кТ, поэтому
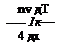
![]() Р =
Р =
Здесь X, как и раньше, представляет собой теплопроводность.
Если предположить, что в металлах тепло переносится только с помощью электронов (что является вполне разумным предположением) и каждый электрон переносит (3/2) кТ единиц энергии, то теплопроводность металла будет равна
![]() Ъпи1к
Ъпи1к
К = --------
4
Коэффициент 3 учитывает тот факт, что реальный газ является трехмерным и электроны имеют три степени свободы. В действительности мы завышаем реальное значение теплопроводности, поскольку не учитываем статистическое! число электронов трехмерного газа, которые пересекают заданную поверхности в единицу времени. Хотя полученный результат и нельзя считать корректны'- в числовом выражении, влияние различных физических факторов на теплопроводность выражено правильно.
Теперь рассмотрим электрическую проводимость
![]() а = qni,
а = qni,
где ц — подвижность, т. е. скорость носителя заряда, соответствующая единично'^ значению электрического поля, вызывающего это движение. Другими словами, это отношение дрейфовой скорости vd к величине электрического ПОЛЯ Е
р = vJE. (38)
В предположении, что соударения изотропны, скорость электрона после каждого соударения статистически равна нулю (поскольку все направления движения равновероятны). В этом случае средняя скорость дрейфа электрона будет равна (1/2)at. где а — ускорение, qE/m, a t— среднее время свободного побега l/v. Вспомним, что тепловая скорость электрона v обычно много больше скорости дрейфа, vd.
р = ql/(2mv) (39)
и
о = q1 nl/(2mv). (40)
Таким образом, отношение
Х/с = 3mv2 k/(2q2) = 3k2T/(2q2), (41)
поскольку
mv2 = кТ. (42)
Точное выражение для искомого отношения имеет вид
Vo = n2/3(k2 T/q2) = LT = 2,44 • КН Т. (43)
Это выражение называется законом Видемана-Франца-Лоренца, а постоянная L = 2,44 ■ К)-8 (В/К)2 — числом Лоренца.
Из этого закона следует, что если уменьшать поток тепла, применяя мате - Іриаїм с более низкой теплопроводностью, то это приведет к автоматическому [ичению электрического сопротивления термопары, поскольку существует пяю пропорциональная зависимость между X и о.
Таким образом, невозможно добиться никакого улучшения путем вариации І ВI их двух параметров, и поэтому у большинства металлических проводников ■ротность зависит только от коэффициента Зеебека и от температуры, К-1
Z = a2/(L Т) = 4,1 ■ 107а2/ Т. (44)
метим, что Z обратно пропорциональна L.
Закон Видемана-Франца-Лоренца носит относительный характер, посколь - 1к> он лишь весьма приблизительно описывает поведение большинства металлов Ш неприменим ко всем материалам. Число Лоренца также не является констан - I т< . как это предписывается теорией — его значение меняется при переходе от ■иеталла к металлу (см. табл. 5.2).
|
■•«лица 5.2. Число Лоренца для некоторых металлов
|
Следует отметить, что точность значений, приведенных в табл. 5.2, невысока, поскольку они получены на основе результатов независимых измерение' теплопроводности и электрической проводимости, опубликованных в Справил нике по химии и физике «Handbook of Chemistry and Physics» (CRC). Скор е всего, измерения теплопроводности и электрической проводимости материал проводились для различных образцов без учета того факта, что электричес проводимость весьма чувствительна к примесям в материале. С учетом этих стоятельств приведенные значения L являются приблизительными.
Дополнительно можно отметить, что теплопроводность чаще всего измеря ется с точностью не выше второй значащей цифры. Важным фактором являет* также предположение о том, что электроны — единственные переносчики теч. в твердом теле. Это предположение с некоторой натяжкой справедливо толь - для металлов и несправедливо для большинства остальных материалов. В даль нейшем мы обсудим эти вопросы более подробно.

 Опубликовано в
Опубликовано в