1. Описание системы н главные предположения. Закономерно­сти самосинхронизации вибровозбудителей, рассмотренные выше на примере простейшей системы, допускают обобщение на значи­тельно более сложные случаи.

Будем по-прежнему рассматривать задачу о простой (некрат­ной) синхронизации вибровозбудителей, но будем считать (см. рис. 5), что последние установлены на произвольной системе твер­дых тел Всі, -.., Bon (несущих тел), связанных между собою и с неподвижным основанием 1 некоторыми «сосредоточенными» гео­метрическими связями 2, а также упругими 3 и демпфирующими 4 элементами. Колебательная часть системы при этом может иметь любое число степеней свободы и не быть непременно линей­ной; считаем, однако, что нелинейные характеристики достаточно гладкие, так что, например, случай, когда несущие тела могут соударяться, здесь исключается. Не будем далее предполагать, что вибровозбудители В і, ..Вк являются простыми дебалансны-
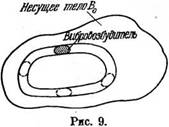
ми — это могут быть теперь любые инерционные возбудители, представляющие собой тела, которые могут совершать периодиче­ские движения относительно какого-либо из несущих тел (рис. 9). Естественно, что вынуждающая сила, генерируемая та­кими возбудителями (назовем их обобщенными механическими возбудителями), даже при неподвиж­ном несущем теле не обязательно является чисто гармонической.

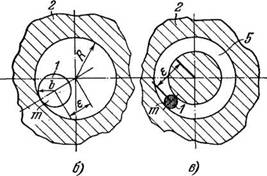
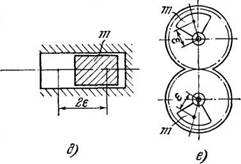
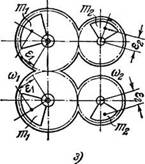
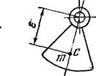
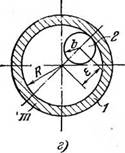
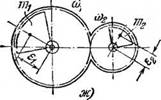
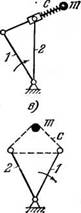
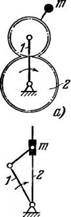
Впрочем, большинство получивших распространение промышленных ме­ханических вибровозбудителей гене­рируют либо гармоническое возбуж­дение, либо возмущение, состоящее из двух или трех гармоник. Некото­рые характерные типы таких возбу­дителей схематически представлены на рис. 10: на рис. 10, а изображен уже рассматривавшийся про­стейший дебалапспый возбудитель (неуравновешенный ротор); на рис. 10, б и 10, в — внутренние планетарные возбудители; на рис. 10, г — внешний планетарный возбудитель (их описание см. в п. 5 § 8); на рис. 10,3 — так называемый поршневой возбуди­тель, в котором вынуждающая сила развивается массой т, воз­вратно-поступательно движущейся в полости корпуса. Наиболее часто, однако, для создания вынуждающей силы постоянного нап­равления используются два дебалансных возбудителя, роторы ко­торых связаны зубчатым зацеплением с передаточным отношени­ем, равным единице (рис. 10, е); такой возбудитель иногда назы­вают самобалансным. Впрочем, как будет ясно из дальнейшего, та же цель часто более эффективно достигается путем использова­ния явления самосинхронизации. На рис. 10, ж изображен бигар - монический возбудитель, ненаправленного, а на рис. 10, з — нап­равленного действия.

Положение инерционного элемента (ротора, поршня и т. п.) каждого из изображенных на рис. 9 и 10 возбудителей относитель­но несущего тела может быть задано всего одной обобщенной ко­ординатой ф,. Будем предполагать, что эта координата может быть выбрана так, что ее изменение в процессе изучаемого синхронного движения представляет собой почти равномерное вращение

<Ps = Cs [(Of - f а, - !- fxty* («г, и)]- (8-і)

Здесь, как и ранее, (о и а, — постоянные, а, = ± 1, а }гф*((оі, р)— слагаемое, характеризующее малые колебания относительно рав­номерного вращения.

Считаем далее, что между валами или инерционными элемен­тами возбудителей могут иметься (не показанные на рис. 9) не­
сомые связи в виде упругих валов, муфт, связей типа электриче­ского вала, а также так называемых центробежно-инерционных

Рис. 10.

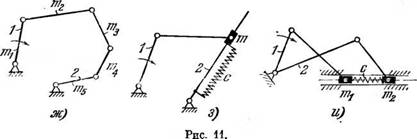
связей или муфт [57, 242, 2561, представленных па рис. 11 в не­скольких вариантах. На этом рисунке звенья 1 связаны с одним из валов (роторов), а звенья 2 — с другим; на рис. 11, а—е изоб-

ражены случаи соосных, а на рис. 11, ж, з — несоосных валов. Ва­рианты, представленные на рис. 11, е—и, отвечают связям с «соб­ственными степенями свободы», а изображенные на рис. 11, а—д — связям без «собственных степеней свободы» (речь идет со­ответственно о том, может или не может изменяться положение

2-

г)

инерционных элементов связей при фиксированных положениях звеньев 1 и 2). Упругие элементы с показаны штриховыми линия­ми или изображены в виде пружин. Отметим, что несомые связи не предполагаются непременно линейными.

Описанная система относится к классу несвободных орбиталь­ных систем и притом таких, в которых несомые тела имеют одну степень свободы относительно тел несущей системы (см. § 6 гл. 12); задача о самосинхронизации вибровозбудителей в этой си­стеме может рассматриваться как задача о синхронизации в си­стеме с почти равномерными вращениями (см. § 4 гл. 12).

Уравнения движения рассматриваемой системы при сделанных предположениях могут быть записаны в форме уравнений (4.2), 6 и. И. Блехман

(4.3) гл. 12, причем уравнения (4.2) для вращательных координат <Рь..., фь представляют собой в этом случае уравнения движения инерционных элементов вибровозбудителей, а уравнения (4.3) для колебательных координат щ, ..в» — уравнения движения несу­щих и несомых связей (сравните эти уравнения с уравнениями (4.12), полученными для частного случая изучаемой системы).

2. Основные результативные соотношения. Характер изучае­мых синхронных движений системы определяется выражениями

(4.1) гл. 12 при щ = щ =... = nh = 1, причем в порождающем приближении

Ф® = as(ffitH-as) (s = l,..., к),

(o. Z)

Ur = Ur ((t)f, CCj, • • •, CCft) (r = 1,..., v),

где ul — периодические с периодом T = 2л/со по времени t ре­шения уравнений

<г = !.•••.'’)• <8-3)

Здесь и ниже, как и ранее, дополнительные, не выполняющие обычную роль круглые скобки означают, что заключенные в них выражения вычисляются для порождающего решения (8.2).

Будем вначале рассматривать задачу о внешней синхрониза­ции, когда обобщенные силы и зависят явным образом

от времени t.

Начальные фазы движения инерционных элементов вибровоз­будителей а і, ..., ак определяются из следующих основных урав­нений (см. равенства (4.6) и (4.7) гл. 12):

Р, (ах,..., aft) = JL (As - Л s)^±- (+ Л) = 0 (8.4)

(s = 1,..., Jc),

тде

Л = <(L)> (8.5)

— усредненная за период Т — 2п/а> на порождающем решении •функции Лагранжа системы, а

4, = Zs — Gs,

Zs = cs <(<?(s1))>, Gs = - 2 (<?(r0)) d~) (8.6)

— избыточный момент, т. e. средний момент неконсервативных сил, приведенный к координате ф, (далее будем условно говорить

о моменте, приведенном к валу s-го возбудителя или просто о мо­менте, действующем на s-й возбудитель).

Рассмотрим отдельно структуру и механический смысл каж­дого из слагаемых основных уравнений (8.4), которые, как и урав­нение (4.6) гл. 12, можно толковать как уравнения равновесия средних моментов, действующих на s-й возбудитель. Величины

J[s(a1,...,cth) = — ~ (8.7)

представляют собой средние потенциальные моменты, действую­щие на возбудители. Поскольку функцию Лагранжа системы в рас­сматриваемой задаче мождо считать не зависящей явным образом от времени і, то имеет место равенство (4.8) гл. 12:

' Іа--І£-0. (8.8)

£—1 t—1 S

Это означает, что моменты Ж, не связаны непосредственно с при­током или убылью энергии в системе; указанные моменты лишь перераспределяют нагрузку между отдельными возбудителями.

Рассмотрим подробнее структуру функции Лагранжа системы и тем самым моментов Ж,. В рассматриваемой задаче функция L может быть представлена в форме

L = L* + Lm + (8.9)

Здесь

ь ft

I* = 2l, + AL*, AL* = 2 ALs% (8-Ю)

S—1 1

где L, = L,(<р„ <р8) — «собственные» функции Лагранжа возбуди­телей, т. е. функции Лагранжа 'возбудителей при неподвижных телах несущей системы и отсутствующих несомых связях, а

AZ/g = Дії, (<ps, (р8‘іЦі,•••, um; Ui, um) (8.11)

— добавки к этим функциям Лагранжа, обусловленные подвиж­ностью тел несущей системы. Под Bj, ..., Um при этом понимают­ся обобщенные координаты, определяющие положение тел несу­щей системы (m ^ v; см. уравнения (8.3)).

Через

La) = La) (uj,..., um; щ,..., Um) ' (8.12)

>значена «собственная» функция Лагранжа несущей системы язей первого рода), а через

L — L (<рь..., <pft; фі,..., qv, xlt. Vi ar1}. •xv) (8.13)

— функция Лагранжа несомых связей (связей второго рода). Как отмечалось, несомыми связями могут быть упругие валы или муф­ты, соединяющие роторы возбудителей, устройства типа электри­ческого вала, а также центробежно-инерционые связи. Эти связи, з отличие от несущих, не приводят к появлению дополнительной подвижности роторов возбудителей; как правило, они вводятся в систему в качестве средств принудительной синхронизации, если эффект самосинхронизации не обеспечивает устойчивость и ста­бильность требуемой фазировки роторов (см. § 11).

Подчеркнем, что зависимость функций ДLs и Ь{11) от <pi, ... —, |ф[21] предполагается такой, что при подстановке вида (8.1) они становятся (или остаются) периодическими функциями of с пе­риодом 2л; поэтому все средние значения функций Лангранжа

л = ІА, + да* + л(1) + л(П} = л* + л(1) + Л(П),

£=1

AS = <(LS)>, л * = <(£*», ДЛ*=<(Д£*)>, (8.14)

л(1) = <(l(I))>, л(П) = <(l(II))>

являются 2я-периодическими функциями каждой из фаз o&i, ...

• • ., CCft.

Поскольку собственные функции Лагранжа каждого возбуди­теля зависят только от обобщенных координат и скоростей этого возбудителя, то

^*=0 (/ = 1, —, к). (8.15)

Поэтому

л дЛ = _ 5^11 — JL (ДА*) (8 16)

да да ’ да да ' >' ' '

S S S S

где fi

Ао = <(і0)> = <(ДІ* + L(I) + L(II)) > = ДА* + A(I) + А(П) (8.17)

— среднее за период значение функции Лагранжа всей системы связей, вычисленное в порождающем приближении.

По своему смыслу момент Ж, в рассматриваемой задаче пред­ставляет собой сумму консервативных частей W(SK) и SiK) вибра­ционного момента и момента системы принудительной синхрони­зации *) (т. е. системы несомых связей):

Jt^W^+S™. (8.18)

§ 8] ОБОБЩЕНИЯ ЗАДАЧИ 85

V

В случае безынерционных связей, когда подвижность несущих тел не сказывается на кинетической энергии элементов несомых связей, можно положить

Я1*,= -‘>(М;+Л<1>>, (8.19)

£ S

Для моментов wi*® и справедливы равенства

2 WiK) = О, 2 SsK) = 0, (8.20)

S=1 *=1

получающиеся так же, как (8.8), и имеющие тот же смысл.

Обратимся к рассмотрению слагаемых As в уравнениях (8.4), т. е. избыточных моментов на валах возбудителей. Величину

Gs = — 2 (^0)) ~да / в изУчаем°й задаче можно трактовать

Г—1 s

как средний момент неконсервативных сил, связанных с ко - лебательными координатами и учитываемых в порождающем приближении. При этом можно положить

Если рассматривается движение вдали от резонанса по коле­бательным координатам, как это предполагалось, например, в § 4, то часто неконсервативные силы (обычно — силы вязкого сопро­тивления) в порождающем приближении можно не учитывать. Тогда

(?г0) = 0 (г = 1, —, v), WiG) = S[G) = Gs = 0. (8.22)

При этом основные уравнения (8.4) значительно упрощаются не только за счет обращения в пуль указанных моментов, по и за счет упрощения выражений для м® (wt, al5 ...,ccft), определяе­мых теперь из уравнений (8.3) при (?£0) = 0.

Наконец, величины Zs = as<(<?i1>)>, которые можно назвать из­быточными моментами на валах возбудителей, в рассматриваемой задаче представляют собой средние значения разности моментов (cs<Ls>), передаваемых от двигателей, и моментов сопротивления

о.<(Д.)> движению инерционных элементов возбудителей:

55 Л—7 мт, т.тгп (г.

г-м.

простейшей задаче, рассмотренной в §§ —'і оыло

Z. = о. <($1})> = <*. <(£s)> - <№)>• (8-23)

формулы (4.20)) j

Z8 = asLs (с4ю) — R°s (со).

В более сложных случаях величины a,<(L.)> и o,<(R,)> могут за­висеть от фаз ссі, ..ак. Так, например, в случае привода возбу­дителей от синхронных нереактивных двигателей

<7* <(£*)> = oaL* [о* («* — Р*)]. (8.24)

Здесь через L* обозначен синхронный момент, передаваемый от двигателя, а через р, — так называемый установочный угол синх­ронного двигателя, выбираемый из условия обеспечения требуемой фазировки движения возбудителей (подробнее о формуле (8.24) см. в книге t57l).

Подобным образом в случае планетарных вибровозбудителей С,<Ш.)> зависит от всех фаз cti, , аЛ в связи с тем, что сопро­тивление движению инерционного элемента возбудителя сущест­венным образом зависит от характера колебаний тела, на котором этот возбудитель установлен. При этом можно положить

<(Д,)> - (со) + WlR) (аъ..., ah), (8.25)

отнеся слагаемое к вибрационному моменту W,, который,

таким образом, представится в виде суммы трех составляющих:

Ws = W[K) + W<E) + Wic (8.26)

одной консервативной и двух неконсервативных. В аналогичном виде представляется и момент Ss, обусловленный паличием несу­щих связей:

S, = S(sK) + SiG}. (8.27)

Конкретные выражения величин и S<K) можно найти

в книге [57]; для некоторых случаев они будут приведены ниже (см. п. 5).

При использовании введенных обозначений и результатов при­веденного анализа основные уравнения (8.4) можно представить также и в одной из следующих эквивалентных форм:

Рв К,..., «ft)=~L[(Ts <(LS)> - R°s (со) - W. ~Ss] = 0 (8.28)

'fs

(s =n 1, . •

Ps (a*,..., = — ^ + Z' - Gs) = 0 (8.29)

(s — k).

Заметим, что как и уравнения (4.19), выведенные в § 4 для част­ного случая, эти уравнения могут быть формально получены пу­тем усреднения правых частей уравнений движения вибровозбуди­телей (см. уравнения (4.2) гл. 12), в которые вместо tp, и и, под­ставлены их порождающие приближения (8.2).

Сформулируем теперь общий результат исследования.

Для возможности синхронных движений изучаемого типа не~ обходимо, чтобы основные уравнения (8.4) (или (8.28), (8.29)) до­пускали вещественные решения относительно ПОСТОЯННЫХ «1, ...

, a, h. Устойчивые синхронные движения будут отвечать лишь

тем решениям указанных уравнений, для которых все корни ал­гебраического уравнения k-й степени

щ — 68jit| = 0 (s, / = 1,..., к) (8.30)

имеют отрицательные вещественные части. При наличии хотя бы одного корня с положительной вещественной частью соответству­ющее движение-неустойчиво, а в случае присутствия нулевых или чисто мнимых корней, вообще говоря, требуется дополнительное исследование.

В случае задачи о внутренней синхронизации (например, о са­мосинхронизации), когда уравнения движения системы автоном­ны, из основных уравнений (8.4) (или (8.28), (8.29)) фазы «і, ...

..., сс* определяются лишь с точностью до постоянной (т. е. опре­деляются лишь разности а.—ah), но зато из тех же уравнений, вообще говоря, находится также исходное приближение к синх­ронной угловой скорости to. Уравнение (8.30) в этом случае не­пременно имеет нулевой корень, который, одпако, не влияет на решение вопроса об устойчивости и легко отделяется, после чего получается уравнение (к — 1)-й степени

-P*d~k) - а**| = 0 (*, / = 1, • • •, к - 1), (8.31)

совпадающее по форме с болёе подробно записанным уравнением

(4.24) (о соответствующем сокращенном обозначении см. сноску в § 2 гл. 10).

Приведем еще уравнение баланса энергии в системе: to 2 о. <(£.)> = to il (R°t + W™ + + S<G)),

8—1 S=1

которое получается в результате сложения всех уравнений (8.27) и учета равенств (8.20), (8.25) и (8.26).

В случае приводимых от асинхронных двигателей дебалансных вибровозбудителей с положительными, не слишком сильно отли­чающимися парциальными угловыми скоростями (см. § 5), и ког-

д - Л<п>)

ЫК) = _ дЛ_ = _ д_ “ да да. S S

wiK) д (ДЛ*

да.

- Л№) дЛ(1^

(8.35)

ДА*,

да„

да силы сопротивления в колебательной части системы не учиты­ваются (<?г0) = 0) имеем G,= 0, W[R) = WlG) = 0, = W[K Zs = ks (cos — oj), (8.32) и уравнения (8.28) резко упрощаются, принимая в точности тот же вид — ®) (“!,•••» ah) = 0 (S = l,(8.33) что и уравнения (5.17); различие состоит лишь в выражениях W, = W™ , которые теперь могут оказаться более сложными, чем (4.20). Складывая уравнения (8.33), предварительно умноженные на к„ придем к тому же соотношению (5.18) для определения син­хронной угловой скорости о; это соотношение и в данном случае играет роль уравнения баланса энергии. 3. Случай квазилинейной колебательной системы. Выражения вибрационных моментов через гармонические коэффициенты влия­ния. Ряд упрощений полученных выше общих соотношений дос­тигается в случае, когда несущая система является линейной, по крайней мере в порождающем приближении. Предположим, что это так и что к тому же несомые связи (элементы системы при­нудительной синхронизации) безынерционны и не вносят допол­нительных степеней свободы. Тогда т = v и выражение (8.13) для функции Лагранжа Lai) не будет содержать переменных щ,_______________ ..и„. Наконец, допустим, что рассматривается движение вдали от резонанса по колебательным координатам п некопсервативпые обобщенные силы, отвечающие этим координатам, в порождающем приближении не учитываются, т. е. выполняются равенства (8.22). При сделанных предположениях справедливы соотношения (4.14) гл. 12, и поэтому при учете (8.14) и (8.16) имеем д (Л + л(1> - Л<н>) _ д (Л* + 2Л<Г>) _ д (АЛ* + 2Л(1>) _ п, я о/ч да — да ~ да S S S Если учесть, что в дайном случае верны также формулы (8.19), то при учете (8.16) и (8.4) будем иметь

В результате основные уравнения (8.4), (8.27) и (8.28) также уп­рощаются и могут быть записаны в одной из следующих форм:

Ps {аи..., ah) ^ j - К <(LS)> - R°s - W[R) - W™» - S™] = 0

(s=l,..., k), (8.36)

0.

Ps (alf <(£s)> - i? s° - И*.*' - dSAm-^

(8.37)

В случае квазилинейной колебательной системы может быть использован эффективный способ получения выражений для виб­рационных моментов Ws, что является наиболее трудным элемен­том при составлении основных уравнений. Этот способ, предло­женный независимо, и в несколько отличающейся форме К. Ш. Ходжаевым [283] и JI. Шперлингом [329, 330], заключает­ся в представлении выражения для Ws через посредство так на­зываемых гармонических коэффициентов влияния.

Будем сначала предполагать, что вибровозбудители являются обычными дебалансными (см. § 1 и рис. 9, а); с другой стороны,

откажемся от предположения о равенстве нулю неконсервативных

сил соответствующих колебательным координатам, а также

от предположения об отсутствии резонанса по этим координатам; будем считать при этом, что силы Qi0) являются силами вязко­го трения. В рассматриваемом случае = 0, т. е. момент

сопротивления os< (/?„)> не зависит от ai, ..., a, h, так что согласно

(8.25) и (8.20

as <(Л5)> = ГГ, Ws = + ТПС). (8;38)

Пусть osusvsws (s = 1,_______ , k) — прямоугольная система коор­

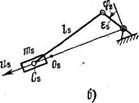
динат, связанная с соответствующим телом несущей системы (рис. 12, а), причем ось osws направлена вдоль оси вращения ро­тора s-то возбудителя, а начало координат os выбрано так, чтобы центр тяжести ротора Се всегда находился в плоскости o, usvs.

Введем в рассмотрение к2 величин

*£«8)И, ЛЙЧю), (со), к№ (со),

ll-wf' («), 1]?ш8)(со), Фгі8-1 («),

определяемых следующим образом.

Пусть к точке несущего тела о, в направлении оси ом, прило­жена гармоническая сила единичной амплитуды с периодом 2л/со. Пусть кроме этой силы на колебательную систему не действуют никакие другие задаваемые силы. Тогда амплитуда проекции пе­ремещения точки os на ось osiis при установившихся вынужден-
пых колебаниях и угол сдвига фаз между указанным перемеще­нием и силой будут соответственно равны величинам к^и (со)’ и (со).

Таким образом, если на колебательную систему в точке о} действует только одна задаваемая сила ij cos cof, то проекция

С
	Us
С

ife

Os

Os

Ряс. 12.

перемещения точки о, на ось оеив в режиме установившихся ко­лебаний будет

4is) = (со) cos [сої - Il4is) (со)]. (8.39)

Аналогичным образом величины кщ> 🙂 (со) И г|#в5) (со) опре­деляются соответственно как амплитуда и сдвиг фаз проекции

перемещения точки os на ось vsvs при действии единичпой гармо­нической силы периода 2л/со на точку о,- в направлении оси osus и т. д.

Введенные коэффициенты могут быть определены в результа­те решения соответствующих линейных задач или даже экспери­ментальным путем (см. ниже). В случае, когда трение в колеба­тельной части системы не учитывается, величины Кии (со), —

№ (со) представляют собой обычные гармонические коэффи­циенты влияния; мы сохраним этот термин также для систем с трением и будем называть указанные коэффициенты гармониче­скими коэффициентами влияния первого рода.

Для гармонических коэффициентов влияния имеют место со­отношения взаимности [283І:

/с(и«} (со) = (со), к^} (со) = (со), (со) = k(J, s) (со),

(8.40)

^uu} (со) = фии' (со), (со) = («), ф™ } (со) = (со).

Отметим, что для определенности фаз Урии, • • •, ) можно счи­тать величины кии, ■ ■ существенно положительными.

Как показал К. III. Ходжаев [283] (см. также [57]), вибраци­онный момент W, для случая дебалансных вибровозбудителей вы­ражается (с точностью до обычно не существенных малых вели­чин) через введенные выше гармонические коэффициенты влия­ния первого рода следующим образом [22]):

W8 = VtfP + W?} =

= 2 тІгІ sin (а« — аІ + ^ии8)) +

+ cos (а„ — аj + — oskuv cos(ae — а,• + +

+ OjOskv^ sin (а, — щ + фіо*5) ]• (8.41)

Здесь, как и в § 4, через т, и е, обозначены соответственно масса и эксцентриситет ротора s-io возбудителя, а число о. = 1, если рассматривается синхронное движение, в котором ротор «-го возбудителя вращается в положительном направлении (см. рис. 12, а), и о, = —1 — если в отрицательном.

Часто удобнее пользоваться не введенными выше гармониче­скими коэффициентами влияния первого рода. •., к$и %

Фгш- • - і а величинами

= Я&> = *2? cos К™ = ЯЙ?> = & cos

к(18) = Kif = cos (8.42)

МІ*) ^(si) „ /.(j*) - u(ie) /ЧІв) __ rf(ei) _ iu(i*) e:n. Ms)

Wuu = — n>iIU Yuu j — «ню ~ kill Yuli j

G[,is) = Gisp — к»»'* sin iJ-'ct>,

использовавшимися JI. Шперлингом в упомянутых работах [329, 330J; назовем эти величины гармоническими коэффициентами влияния второго рода. Очевидно, что по своему физическому смыслу, например, величины Кии И Сии представляют собой коэффициенты соответственно при cos of и при sin at в выраже­нии Suu' для проекции смещения точки о. на ось оеи, при дей­ствии на точку О] гармонического возмущения единичной ампли­туды, направленного вдоль оси о, и. Иными словами, при действии указанного возмущения проекция смещения «uif точки о, на ось

osu представляется не в виде (8.39), а в форме Suu — Кии cos at + G(uu sin at.

Нетрудно видеть, что соотношения (8.42) непосредственно вы­текают из сопоставления последнего равенства с (8.39).

При использовании гармонических коэффициентов влияния второго рода выражение (8.41) для вибрационных моментов мо­жет быть представлено в форме

W. = W[K) + W*G) =

4

= 2 mi( j I (^«} — vfivu + efiuv + OjGsKlv3^) sin (as — aj)-b

5=1

+ (Gg? + - csKuv + cpfi™) cos (a, - щ)]. (8.43)

Отметим, что в случае, когда рассматривается движение вда­ли от резонанса по колебательным координатам и силы трения в порождающем приближении не учитываются, все величины tyuu, • • • і "Фет?* равны либо 0, либо я (напомним, что коэффициенты кии,• • •, * считаются существенно положительными). Поэтому

в указанном случае

W

(G) /-> /-i(is) /4js) /і<js) /-i(js)

s — U, Ituu — uU|j — 'Jmt •— — U,

и выражение (8.43) упрощается:

4 к

ws = WiK) = 2 i(Kuu + Sin (a, - Щ) +

S=1

+ (o}K^ - asK^>) cos (a, - a})]. (8.44)

Рассмотрим теперь случай вибровозбудителей направленного действия — так называемых поршневых вибровозбудителей, схе­матически представленных на рис. 10, д и 12, б. Колебания инер­ционному элементу ms («поршню») в этих возбудителях сообща­ются, например, от центрального кривошипного механизма. Отношение радиуса кривошина е„ к длине шатуна I, при этом будем считать столь малым, чтобы движение массы ms при рав­номерном вращении вала кривошипа можно было рассматривать с достаточной точностью как простое гармоническое. Начало под­вижной оси о. и, выберем в среднем положении массы тпв при ее колебаниях в несущем теле. В данном случае достаточно исполь­зовать лишь два гармонических коэффициента влияния первого рода кии и • Первый из них равен амплитуде проекции пере­мещения при колебаниях точки о,- несущего тела на ось о, и, выз­ванных гармонической силой единичной амплитуды с периодом

Т = 2я/(о, действующей на точку о8 вдоль оси osus; есть со­

ответствующий угол сдвига фаз. При этом получается следующее выражение для вибрационного момента:

W. = W™ + wiG) =

с mew

л h

2 kuuGjirijEj sin (as — a, j + грии'). (8.45>

3=1

При использовании гармонических коэффициентов влияния второго рода, определенных соотношениями

(8.46)

выражение (8.45) принимает вид

Как и ранее, при неучете сил вязкого трения в колебательной

ws = wiK) + TF<G> =

і)]- (8.47)

части системы в нерезонансном случае W(sc J = 0, Gffl = 0 ив

выражении (8.47) под знаком суммы остается лишь первое сла­гаемое.

Как и в § 5, все полученные выражения для вибрационных моментов могут быть представлены в виде сумм частных вибра­ционных моментов wtj, имеющих, естественно, тот же физиче­ский смысл.

Заметим в заключение, что выражения для вибрациоппых мо­ментов через гармонические коэффициенты влияния могут быть получены и для других, более сложных типов возбудителей, в частности, для возбудителей, генерируюіцих возмущающие силы и моменты весьма общего характера [214].

4. Интегральный критерий устойчивости (экстремальное свой­ство) синхронных движений и тенденция вибровозбудителей к синхронизации. Сказанное в § 7 по поводу самосинхронизации вибровозбудителей в простейшей системе распространяется на значительно более общие системы, рассмотренные в настоящем параграфе.

Для справедливости интегрального критерия устойчивости (экстремального свойства) в общем случае достаточно, чтобы существовала функция В (потенциал усредненных некопсерва - тивных сил) такая, что

Тогда согласно изложенному в § 8 гл. 10 и в § 4 гл. 12 за потен­циальную функцию можно принять выражение

D = -(A + B); (8.49)

точкам грубых минимумов этой функции отвечают устойчивые синхронные движения вибровозбудителей.

Поскольку собственные усредненные функции Лагранжа воз­будителей А, не зависят от ai, ..., а* (см. п. 2), то за функцию D можно принять также выражение

D = - (А0 + В) = - (ДА* + А«) + А<п> + В), (8.50)

в котором Ао = ДА* + А{1) + А{11) есть усредненное значение функции Лагранжа системы связей.

В случае, когда система квазилинейна по колебательным ко­ординатам, а консервативные силы по этим координатам не учи­тываются (рассматривается движение вдали от резонанса), спра-, ведливы соотношения (8.34), и поэтому за потенциальную функ­цию может быть принято, кроме (8.49) п (8.50), также одно из следующих выражений:

D = Ат _ - В, (8.51)

D = - ДА* + А<п> + в), (8.52)

где дВ/даа = As = Zs. При этом в случае самосинхронизации де­балансных и подобных им возбудителей, когда несомые связи от­сутствуют Л(Ш = 0, а парциальные угловые скорости одинаковы,

как п в § 7, В = const, и поэтому можно положить

D = Л(Т> или D = —ДА*. (8.53)

Иными словами, в этом весьма распространенном случае за по­тенциальную функцию можно принять либо усредненную за пе­риод функцию Лагранжа системы несущих тел, либо взятую с противоположным знаком добавку к функции Лагранжа возбуди­телей, обусловленную подвижностью несущих тел; при этом функции Лагранжа предполагаются вычисленными в порождаю­щем приближении.

В еще более частном, однако нередко встречающемся на прак­тике случае, когда тела несущей системы связаны одно с другим и с неподвижным основанием весьма мягкими упругими элемен­тами (геометрические связи между теламп, однако, могут присут­ствовать), потенциальной энергией П(1) несущей системы можно пренебречь, и тогда согласно первому выражению (8.53)

D = <(2,(1))>. (8.54)

Таким образом, в данном случае устойчивые синхронные движе­ния отвечают минимумам усредненной за период кинетической энергии тел несущей системы. В частности, если возможна такая фазировка возбудителей, при которой калебания несущей систе­мы будут отсутствовать (в порождающем приближении), то имен­но она и окажется устойчивой. Это положение, обобщающее из­ложенное в § 7 и названное парадоксом неработающих связей, находит важные практические приложения (см. § 14).

Второму выражению (8.53) соответствует геометрическая фор­ма интегрального критерия устойчивости, предложенная Б. П. Лав­ровым ([164, 165J; см. также [57]). Оказывается, что величина —ДА* в рассматриваемых системах представляет собой «потерю» кинетической энергии вращающихся роторов, обусловленную колебаниями их осей. При этом минимуму выражения —ДА* = = —ДТ* соответствует минимум суммы амплитуд проекции пере­мещений точек о, (рис. 11, а) на направление вектора-эксцентри­ситета ротора 8 Напомним, что в случае задачи о внутренней синхронизации (в частности, о самосинхронизации) из условий стационарности функции D

щ = - Р. («1, • •а*) = 0 (* = 1 к) (8.55)

определяются разности фаз а, — ак, а также исходное приближе­ние к синхронной угловой скорости ю.

Тенденция к синхронизации вибровозбудителей в рассмотрен­ных системах предопределяется 2я-периодичностью функций Л, До, ДЛ*, Л(1) и Л(П> по всем фазам ai, ..., ah. А именно (см. § 9 гл. 10), если, например, величины А, равны нулю или малы со­ответственно по сравнению с дЛо/да„ d(Am — A(II))/5as или

д ДА* 4- Л(П)') jdas, т. е. если существует периодическая по­тенциальная или квазипотенциальная функция, то устойчивые в малом синхронные движения непременно существуют. Это, в частности, будет в случае дебалансных или аналогичных им вибровозбудителей с одинаковыми или близкими парциальными угловыми скоростями Os.

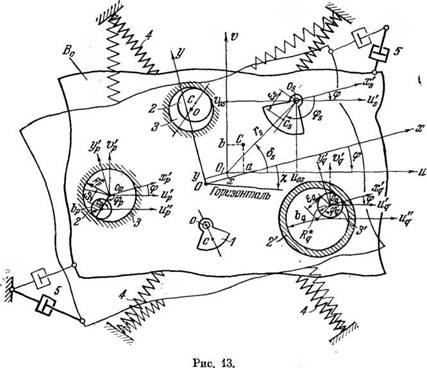
5. Синхронизация вибровозбудителей на упруго опертом плоско колеблющемся твердом теле. Широкий класс вибрацион­ных устройств может быть идеализирован в виде системы, схема­тически представленной на рис. 13. Несущее тело В0 (вибрирую­щий орган машины) считается твердым телом, которое может совершать малые плоско-параллельные колебания и которое свя­зано с неподвижным основанием системой упругих и демпфиру­ющих элементов. В теле размещено к' дебалансных и к" плане­тарных вибровозбудителей, общее число возбудителей, таким образом, есть к = к' + к".

Дебаланспые возбудители 1, как отмечалось в § 1, представ­ляют собой неуравновешенные роторы, приводимые от каких -

либо двигателей. Под планетарными возбудителями понимаются либо круговые цилиндрические ролики 2, вложенные в стаканы 3, укрепленные в теле В0 (внутренние планетарные возбудите­ли), либо кольца 2', которые могут обкатываться своей внутрен­ней поверхностью по осям 3связанным с телом В0 (внешние

планетарные возбудители). Оси возбудителей считаются перпен­дикулярными плоскости, параллельно которой происходит движе­ние тела Во. Предполагается, что в рассматриваемых синхронных движениях ролики планетарных возбудителей не отрываются от стакапов, а кольца — от осей, т. е. что не происходит нарушения неудерживающих связей, Условия, при которых последнее требо­вание выполняется, указаны в книге [57]. Инерционные элемен­ты возбудителей (роторы, ролики, кольца) могут быть связапы друг с другом системой линейно упругих синхронизирующих эле­ментов (несомых связей).

Приведем основные соотношения, относящиеся к задаче о син­хронизации в описанной системе; эта задача подробно изучена в работах [36, 57].

Пусть uOv — система осей, жестко связанных с несущим те­лом начало которой 0 выбрано в центре тяжести так называ­емого вспомогательного тела, т. е. тела, получающегося из В о, если присоединить к нему массы тпг всех инерционных элемен­тов возбудителей, сосредоточив их на осях возбудителей. Пусть далее хОу — неподвижная система осей, с которой совпадают оси иОiv в положении статического равновесия системы. Наклон осей будем выбирать так, чтобы квазиупругий коэффициент с*„ в вы­ражении для потенциальной энергии П(1) нёсущего тела Во был равен нулю (см. ниже). Подобный выбор осей позволяет несколь­ко упростить приводимые далее соотношения. Плоскость хОу не предполагается непременно вертикальной — потенциальную энергию силы тяжести инерционных элементов возбудителей в изучаемом ниже случае задачи можно не учитывать [57].

За обобщенные координаты несущего тела Вс примем коорди­наты х и у точки 0 в системе хОу и угол поворота тела <р, от­считываемый по ходу часовой стрелки; так же отсчитываются от неподвижной оси Ох и углы поворота «р, инерционных элемен­тов возбудителей. Выражения для кинетической - и потенциальной энергии системы имеют вид

к

T=2rs+ тт + ДГ*, П = П№ + №п>, (8.56)

Т — ± Г ^ Г*1) — J Л/Г/Х.2 і,*2 г 1

где

у /Ж. Г1' = ~ М (z2 +y2) + j /Ф2

k

Д77* — — т8гуср., (х sin ср., у cos фЛ

к

Xl];

nh«scos(<pt 4- — |; (8.57)

nm = J {cxx2 - f Суу2 -]■ сфф2 - f 2cxtfxq> + 2cy<Pi/(p),

k k

n(ii) = ± 2 2 с*-, (°s<Ps — Ojqpj — xs + щ)2,

" S=1 j=1

причем ms, Is и є* — соответственно массы, приведенные момен­ты инерции и эксцентриситеты возбудителей; г, и 6, — полярные координаты осей возбудителей (см. рис. 12), М и I — масса и мо­мент инерции вспомогательного тела; Ъ:, = 11.,—es—радиус ро­лика в случае внутреннего и bs = Rs + es — внутренний радиус кольца в случае внешнего возбудителя{Rs— радиус стакана или 7 И. И. Блехман
оси); X* = 1, если ролик или кольцо катятся без скольжения, и Ks = 0, если они скользят, не поворачиваясь, относительно несу­щего тела Во; ha — 0 для дебалансных и ft, = l для планетарных возбудителей; с*, ..., ст — квазиупругие коэффициенты; csj — жесткости, а к* — «установочные углы» системы упругих синхро­низирующих элементов; указанные углы могут назначаться про­извольно — их выбор определяется требуемой фазировкой воз­будителей.

Пусть рассматривается движение вдали от резонанса, т. е. ча ­стоты свободных колебаний тела Во на упругих элементах рі, рг и рз в достаточной мере отличаются от целых кратностей синх­ронной угловой скорости возбудителей to. Силы сопротивления по колебательным координатам в порождающем приближении при этом не учитываем {Qx^ = = 0).

Тогда порождающее решение соответствует равномерному

вращению инерционных элементов возбудителей по закону — = crs(cof + as) (как и ранее, рассмаривается простая синхрониза­ция) и малым установившимся вынужденным колебаниям тела В0 при указанном движении возбудителей. Эти колебания нахо­дятся как 2я/(о-периодическое решение уравнений

k

Мх° + схх° + сХф(р° = 2 COS (cof + as),

s=l

*

My0 - f cyy° - f cmrp° = — 2 cfbmse. sco8 sin (cof 4- a£), (8.58)

S=1

k

/<p° -1-<УР° - Г С*фж° -f СууУ0 = 2 ст£7?г, є8гьсо2 sin (cof + a8 -|- a А),

s=l

которое имеет вид h те

Ж0 = 2 ~ir cos + “*) + G$B° sin + “*)]»

«= 1

k

2

m. e. r о о і

-jjjr- [с, cos ({Of 4- as) - f asDs sin (cof - f as)J, (8.59)

r0 _ V ^ Mp

S“1

2 TT7- Гл/* cos (tot 4- аЛ c*iV° sin (соt + a,)].

Здесь обозначено

A°s = A°s (co2) = bxx (co2) 4- bxф (co2) vs sin 6S, B° = B°s (co2) = — bxy (co2) -1 (со2) vs cos 8S

C°i= C°s (ffl2) = ЪХу (со2) + Ъу(р (to2) vs sin 8S,

D° = D° (со2) = — byy (to2) + byy (to2) vs cos 6S( (8.60)

M°s = (со2) = bX(f (со2) + Ьфф (со2) vs sin 6S,

iVs° = iV° (со2) = — by4> (со2) + Ьфф (со2) vs cos 6S;

= rjp, p2 = I/M;

ЬХХ(С0)_ д { > D(CO2)

Ъ (о2)_Р»2 b

bxy(o)- д(и2) , д(и2)

ь (Ю2)_И-^2) b

byy ((Л)- d^2) со, &фф - в(щ2)

£ (/>*) = {pi-P2) {pi - рг) {pi P'2) ~ - pU {p* —P2) —pit (РІ-Р2);

n2 — °Л r>2 — ^ r,2 _ C4> n2 _ D2 —

Рх ~ M' M’ P<t — I ■> Pxф — Mp’ Fj/<p Mp’

причем согласно предположению частотное уравнение Dip2) = О не имеет корней р, равных /гсо (/г — целое число), так что, во всяком случае, £)(со2) Ф 0.

Выражения для вибрационных моментов Ws, моментов. S's си­стемы принудительной синхронизации и моментов сопротивления Rs имеют вид

w. = w^+wi”

с г(Ю дЛ(и)

s ' да — ^ Csj {as aj Xs і Kj);

s j=l

9 k

ттг(К) 0Am і m e. ci) ^

W s = = у —тзгз [Psi sin (as — a,) + Qsj cos (as — a,-)],

s.7=1

2

f ^ f ffl 6 CO ж 1

W, ' = у Zis/s 2 [Psj cos (as — aj) — Qsj sin (as — otj)];

i=і

#° = т, е8сй2 [у /6cZ, + /г, (/'es — y /Л) , (8.61)

Где

Psi ~ P js = &xx ^s^jbyy “j - Ьх(р (Vj Sill 8 j - f - Vs Sill 6S) —

— bmasGj (Vj COS 6 j -+- vs cos 65) + ЬффО^г^ cos (as6s — (r,6;),

Сії = — Qu = (<т* — Ci) bxy + br>T. (c,-Vj cos 8j — a. vs cos 6Л 4- (8.62)

~r byф (asVj sin 6; — CTjV* sin Ss) + ЬСгфО.;asVjVs sin (оД — Oj6j),

7* а через /« и fs обозначены соответственно коэффициент трения в подшипниках качения дебалансного возбудителя и коэффици­ент сопротивления перекатыванию в планетарном возбудителе (принимается, как обычно, что в первом случае момент сопро - 1 * / • тивления равен у f»dsNs sgn ф5, а во втором /sesiV5 sgn ф8, .гдей,—

диаметр внутреннего кольца подшипника качения, a Ns — модуль нормальной составляющей реакции в подшипнике). Напомним, что для дебалансных возбудителей й, = 0 и W(SR^ — 0.

Основные уравнения, из которых определяются начальные фа­зы а», при этом записываются в форме (8.36) или (8.37), а воп­рос об устойчивости решается в зависимости от знаков веществен­ных частей корней уравнения (8.30) или (в случае задачи о внут­ренней синхронизации) уравнения (8.31).

Заметим, что в случае планетарных вибровозбудителей потен­циальная функция не существует [57]; здесь речь может идти лишь о квазипотенциальной функции в смысле, указанном в § 9 гл. 10.

6. Режимы установления синхронных движений вибровозбу- дителей. В ряде случаев представляет интерес изучение не толь­ко устойчивых установившихся режимов синхронного движения вибровозбудителей, но и процессов установления таких режимов. Дифференциальные уравнения указанных переходных процессов могут быть легко получены путем применения метода прямого разделения движений или вариационного метода А. И. Лурье, (см. §§ 3 и 6 гл. И).

Используя первый метод заметим, что система уравнений

(4.2) , (4.3) гл. 12 для задачи о простой синхронизации (щ =... = = пк= 1) может быть записана в форме (сравните эти уравнения с уравнениями (4.12) настоящей главы, соответствующими про­стейшей задаче)

^Ф* + К (ф* — (Ts(d) = рФ8 (ф8, в, tof) (s = 1, ..., к),

k

Da = 2 (фз) + [iV (и. Фі, • ■ *, Фь), (8.63)

8=1

где D — некоторый дифференциальный оператор, а функции Ф„

Fs и U могут зависеть не только от ф„ и и, по и от их лропэ-

водных.

В соответствии с основной предпосылкой метода предположим,

что рассматриваемые движения могут быть представлены в виде

Ф« = о* - Ь as (t) + 'Ф* (£, wf)]. и = п (t, Ш). (8.64)

где a At) — медленно, a i]:s ив — быстро изменяющиеся величи­ны; возможность такого представления решений уравнений (8.63), близких и синхронным, подтверждается экспериментами (см. § 13).

Считая, согласно замечанию 2) § 3 гл. 11, моменты цФа быст­рыми, запишем уравнения (3.8) и (3.7) гл. 11 в форме

Isas + ksas = jios <Ф8> (s = 1, ..., к), (8.65)

= №(ф« — <Ф«» (s = 1к), (8.66)

ft ' 1

Du = 2 Fs los («Є + + %)] +

«=1

+ tJJ [в, сг (toЄ-+ + Vi), . ■ •, Oft (toe + ak +

Разыскивая вначале 2п/е»-периодическое решение уравне­ний быстрых движений (8.66) при «замороженных» медленных переменных as, будем иметь = 0, а для вектора в0 получим уравнение

к

Du° = 2 Fs [os (toe + as)], (8.67)'

S~1

соответствующее 2л/©-периодическим колебаниям несущей си­стемы тел под действием возбудителей, движущихся по закону Фа = о, (<оЄ + as). Предполагая, что такое решение в0 существует и асимптотически устойчиво, подставим его в правые части урав­нений медленных движений (8.65) вместе с Ф« = ф®. Тогда полу­чим уравнения (напомним, что дополнительные, не играющие обычной роли круглые скобки, в которые заключено обозначение функции, означают, что она вычисляется для порождающего ре­шения ФІ-, Ви)

I£&8 Ч" = pos ^(Фв)^ (s — 1, ..., /с),

или согласно равенствам (4.6) гл. 12

Isas + ksas = ksPs {щ, ..., ah) = - f As (s = 1, ..., к). (8.68>

Таким образом, дифференциальные уравнения медленных про­цессов установления синхронных движений вибровозбудителей легко составляются, если известны выражения для порождающих функций Рв; напомним, что эти выражения даются помимо (8.68} также формулами (8.28) и (8.29), а в случае квазилинейной ко­лебательной системы — формулами (8.36) и (8.37). В стационар­ном случае о:л = const (8.68) приводит к соответствующим оспов-

пым уравнениям. По крайней мере при пренебрежимо малых Isas, а также в случае существования потенциальной функции D из (8.68) получаются и условия устойчивости, выражающиеся через посредство уравнений (8.30) или (8.31) (см. п. 2 § 6 гл. 12).

Как явствует из изложенного в п. 2 § 6 гл. 12, уравнения медленных движений вида (8.68) получатся и в результате ис­пользования вариационного метода А. И. Лурье: изученная не­свободная орбитальная система может рассматриваться как соот­ветствующая система с вибровозбудителями.

На основе уравнений (8.68) можно выполнить апостериорную проверку допущения о медленности переходных процессов, опи­сываемых этими уравнениями. Используя приведенные выше вы­ражения для вибрационных моментов, нетрудно заключить для задачи о самосинхронизации вибровозбудителей вдали от резо­нанса колебательной части системы, что частоты свободных колебаний роторов вблизи стационарных синхронных режимов р, получающиеся согласно (8.68), имеют порядок toУт/М (т — масса ротора возбудителя, а М—масса всей системы). Посколь­ку М~> т, то /з/to < 1, т. е. эти колебания действительно являют­ся медленными.