Вынужденные колебания под действием гармонической силы
 13 сентября, 2014
13 сентября, 2014  Mihail Maikl
Mihail Maikl Вынужденные колебания под действием гармонической силы. Режимы медленных, быстрых и резонансных колебаний. Амплитудно-частотные и фазо-частотные характеристики. Баллистический режим колебаний. Установление колебаний. Характеристики различных колебательных систем. Параметрические колебания. Автоколебания.
В предыдущей лекции мы рассмотрели свободные затухающие колебания, возникающие при начальном кратковременном воздействии внешних сил на колебательную систему. Между тем, в повседневной практике мы сталкиваемся с незатухающими колебаниями, для поддержания которых необходимо подводить энергию к колебательной системе, чтобы компенсировать ее энергетические потери.
Одним из распространенных способов поддержания незатухающих колебаний является непрерывное воздействие на колеблющуюся массу периодической силы (вынуждающей силы)
F (t) = F (t + T), (2.1)
меняющейся во времени t, вообще говоря, произвольно в пределах периода длительностью T. Если, например, такую силу приложить к колеблющейся массе описанного выше пружинного маятника (рис. 2.1), то уравнение ее движения примет вид:
ms = —rS — ks + F (t). (2.2)
|
Fit) |
|
/777777777777^7777777/77 0 Рис. 2.1. |
|
2р Ynt+У n |
Опыт показывает, что если сила внезапно начинает действовать (например, в момент времени t = 0), то маятник начнет постепенно раскачиваться, и спустя какое-то время его колебания установятся. По порядку величины время установления таких вынужденных колебаний будет совпадать с временем затухания t = 5-1 = 2т/Г. Далее мы сконцентрируем внимание именно на установившихся колебаниях. Естественно, что параметры таких колебаний будут зависеть от конкретного вида силы F(t). Из математики хорошо известно, что любую периодическую функцию можно представить в виде ряда Фурье:
F(t) = E F0n sin
n=0
Физический смысл этого представления состоит в том, что периодическое воздействие F(t) эквивалентно одновременному воздействию постоянной силы F00 и набора гармонических сил с соответствующими амплитудами F0n, начальными фазами yn и
2p „ , 2p
частотами wn = ~n = wn, кратными низшей (основной) частоте w = — .
Чтобы получить полную картину вынужденных колебаний под действием силы
(2.3) , необходимо принять во внимание линейность уравнения (2.2). Это позволяет представить его решение s(t) как сумму гармонических колебаний:
(2.3)
|
2p -nt + j n |
|
Sin |
|
(2.4) |
|
s(t) = Ё |
|
n=0 |
происходящих с установившимися амплитудами sQn и фазами jn на частотах wn соответствующих гармоник вынуждающей силы (2.3). Каждое слагаемое в (2.4) может рассматриваться как вынужденное гармоническое колебание, происходящее под
„ „ 2я
действием внешней гармонической силы с амплитудой F0n и частотой wn = ~7^п-
Амплитуды sQn и фазы jn требуют определения, и мы перейдем сейчас к их нахождению.
Вынужденные колебания под действием гармонической силы. Пусть внешняя сила меняется по гармоническому закону
F(t) = F0 sin wt. (2.5)
Уравнение (2.2) в этом случае принимает вид:
ms = - Г,& - ks + F0 sin wt. (2.6)
Под действием этой силы маятник в установившемся режиме будет совершать гармонические колебания
s(t) = s0 sin(wt + j0). (2.7)
Как показывает опыт, амплитуда so и начальная фаза jo (т. е. сдвиг фазы между смещением s и силой F) установившихся колебаний зависят не только от амплитуды силы Fo (что очевидно из уравнения (2.6)), но и от того, насколько частота вынуждающей силы w отличается от собственной частоты колебаний маятника w0 = - Jk/т. Наиболее сильно маятник будет раскачиваться, когда эти частоты практически совпадают: w » W0.
Прежде чем приступить к нахождению s0 и j>0, заметим, что для механических колебательных систем не так просто с технической точки зрения осуществить
0 x 0 s воздействие гармонической силы непосредственно на
движущуюся массу. Гораздо проще это сделать для электрических и оптических колебательных систем, например, для колебательного контура, подключенного к внешнему источнику переменного напряжения. Легко, однако, видеть, что можно поддерживать вынужденные колебания маятника, изображенного на рис. 2.1, иным способом, не прикладывая непосредственно внешнюю силу F(t) к массе т. Достаточно лишь эту силу приложить к левому концу свободной пружины так, чтобы этот конец двигался по гармоническому закону X(t) = ^sinwt (рис. 2.2). Тогда удлинение пружины составит величину s - X, а сила упругости, приложенная к массе т, будет равна - k(s - X). Поэтому уравнение движения массы m запишется в виде:
ms =—rs — k (s — X). (2.8)
Если принять во внимание, что сила упругости пружины в отсутствие смещения груза (s = 0) равна
F(t) = kX(t) = kX0 sin wt, (2.9)
то уравнение (2.8) полностью эквивалентно уравнению (2.6). Сила (2.9) выполняет роль внешней гармонической силы в классической схеме, изображенной на рис. 2.1. Эта сила
легко может быть визуализирована, поскольку ее величина и направление однозначно определяется смещением подвижного левого конца пружины. Это, в свою очередь, дает возможность наглядно продемонстрировать фазовые соотношения между силой F(t) (или смещением X(t)) и смещением s(t) колеблющейся массы.
Перепишем уравнение (2.8) следующим образом:
2F
s + 2§s + wQ s = —-sin wt, (2.10)
m
где F0 = kX0.
Решение этого уравнения будем искать в виде гармонического колебания (2.7), где амплитуда s0 и фаза j>0 могут быть определены, если подставить (2.7) в (2.10). Мы сделаем это несколько позднее, а пока рассмотрим три важных режима вынужденных колебаний.
Медленные колебания. Если частота вынуждающей силы w значительно меньше w0, то скорость s и ускорение s колеблющейся массы будут очень малыми. Поэтому можно пренебречь первыми двумя членами в левой части уравнения (2.10) и записать его в приближенном виде:
2 F0
wQ s = —-sin wt. (2.11)
m
Его решение очевидно:
F0 F0
s(t) = —-2 sin wt = —sin wt. (2 12)
mw02 k
В этом режиме смещение груза пропорционально внешней силе и не зависит от величины его массы т. Решение (2.12) является, по существу, математическим выражением закона Гука для статической деформации пружины. Поэтому этот режим можно назвать квазистатическим (почти статическим). Амплитуда колебаний в соответствии с этим законом равна s0 = F0/k, а смещение s(t) изменяется в фазе с внешней силой.
В схеме, изображенной на рис. 2.2, это эквивалентно тому, что смещение массы m практически повторяет смещение левого конца пружины:
F kX
s(t) = —sin wt = —— sin wt = X(t), (2.13)
kk
поскольку F0 = k^0. Это и не удивительно, т. к. для движения массы m с пренебрежимо малым ускорением s не требуется больших деформаций пружины: s(t) — £(t) » 0.
Быстрые колебания. Если w >> w0, то период вынужденных колебаний T = 2p/w мал. Это означает, что масса m испытывает действие лишь внешней силы F(t), а сила упругости ks и вязкого трения Гs малы. Действительно, за половину короткого периода колебаний, когда масса движется в одном направлении, она не успевает набрать как заметную скорость s, так и сместиться на достаточную величину s от положения равновесия. Поэтому в уравнении (2.10) можно опустить члены, содержащие s и s, и записать его в другом приближенном виде:
.. F0 .
s = —sin wt. (2.14)
m
Интегрируя это уравнение два раза, находим закон движения колеблющейся
массы:
F F
s(t) =------------- 02 sin wt = —02 sin(wt — я). (2 15)
mw mw
Из (2.15) следует, что смещение по отношению к внешней силе запаздывает по фазе на я (jo = - я), а амплитуда, как мы и предполагали, убывает с увеличением частоты.
В схеме, изображенной на рис. 2.2, в таком режиме левый подвижный конец пружины и масса m всегда движутся в противоположных направлениях:
s(t) = ^~~2 sin wt = —^2X(t). (2.16)
mw w
По абсолютной величине смещение массы m в w2/ w2 >> 1 раз меньше смещения левого конца пружины, т. е. практически не будет заметным.
Резонансный режим. Если частота w » wo, то вынужденные колебания происходят на собственной частоте колебаний. Это означает, что
s+w2 s = 0. (2.17)
Следовательно, уравнение (2.10) при учете (2.17) примет вид:
F
2ds = —0sin w0t. (2.18)
m
Интегрируя его, получаем выражение для смещения:
F0
s(t) = 2§m°w sin(w0t — V2). (2.19)
Последнее выражение удобно переписать в виде
F0
s(t) = -0 Q sin(w0t — я/ 2), (2.20)
k
я
где Q = ^z; — добротность маятника. Если добротность Q >> 1, то амплитуда колебаний оТ
может во много раз превышать амплитуду медленных квазистатических колебаний (сравните с (2.12)). Поэтому такой режим называется резонансным.
Велики также амплитуды скорости и ускорения. Поскольку скорость s& , как следует из (2.18), изменяется в фазе с внешней силой, то с энергетической точки зрения это весьма благоприятно для «подкачки» энергии в колебательную систему. Работа внешней силы за период колебаний равна:
T 2 T 2
A = J F(t) • s(t)dt = J sin2 w0tdt = (2.21)
0 2om 0 4om
и значительно превосходит работу этой силы в обоих рассмотренных выше режимах.
Такая большая работа необходима для компенсации значительных потерь из-за силы
вязкого трения.
Для большей наглядности последнего результата обратимся к схеме с подвижным левым концом пружины, где, как это видно из решения (2.20),
s(t) = X 0Q sin(w0t — p 2). (2.22)
Амплитуда смещения правого конца пружины в Q раз превосходит амплитуду смещения левого конца. При прохождении массой m положения равновесия s = 0, когда ее скорость максимальна, левый конец пружины смещен на максимальную величину X0 в направлении скорости движущейся массы. В этот момент времени мощность силы упругости пружины имеет максимально возможное положительное значение при заданной величине X0. В последующие моменты времени эта мощность будет оставаться положительной, что, естественно, обеспечивает наиболее эффективную передачу энергии движущемуся с трением телу.
Если сила (2.5) меняется с произвольной частотой w, то амплитуда s0 и фаза Ф0, входящие в решение (2.7), могут быть найдены, как было сказано выше, подстановкой решения (2.7) в уравнение (2.10). Такую подстановку можно осуществить наиболее просто, если воспользоваться методом комплексных амплитуд, широко применяемым в различных областях физики: теории колебаний, теории волн, электромагнетизме, оптике и др.
Метод комплексных амплитуд. Если в формуле Эйлера (1.53): e1'j = cos j + isin j под j понимать фазу гармонических колебаний
j = wt + j0, (2.23)
то каждому такому колебанию s(t) можно поставить в соответствие комплексное число $(t) = s0ej = s0ej0eiw = s0 cos(wt + j0) + is0 sin(wt + j0). (2.24)
Из (2.24) видно, что решение (2.7) является мнимой частью комплексного выражения: s(t) = s0 sin(wt + j0) = ImsV“ , (2.25)
где s0 = s0eij0 — комплексная амплитуда, которая несет информацию об амплитуде s0 и
начальной фазе Ф0 колебаний. Надо отметить, что метод комплексных амплитуд является, фактически, аналитическим выражением метода векторных диаграмм. Если в последнем методе колебание с частотой w полностью задается вектором s0, то в методе комплексных амплитуд колебание задается числом s0 на комплексной плоскости. Поскольку с комплексными числами удобно и просто производить математические операции, то мы используем это обстоятельство для получения решения уравнения вынужденных колебаний (2.10).
Вынужденные колебания с произвольной частотой. Будем искать решение уравнения (2.10) в комплексном виде:
s(t) = . (2.26)
Вынуждающую силу в правой части (2.10) также запишем в комплексной форме:
F (t) = F0eiwt, (2.27)
где F0 = F0 — действительное число, поскольку для простоты мы положили, что начальная фаза в выражении для силы (2.5) равна нулю.
|
Тогда уравнение (2.10) можно записать в виде: |
|
1 0 iwt |
|
(2.28) |
|
s + 25s + w 0 s — |
Комплексную амплитуду s0 = s0eij0 легко находим подстановкой (2.26) в (2.28):
/ ^2 , о і ^2л /юг F0 іюг
|
(2.29) |
(-w + 2-5w + w 0) s0e =— e
|
(2.30) |
Отсюда получаем:
0 m(w 0 — w2 + 2i5w)
Из (2.30) нетрудно найти амплитуду колебаний s0 = |s0|
|
(2.31) |
|
и фазу j0 = arg s0 : |
|
(2.32) |
|
Re s0 |
|
^/(w;5 — w2)2 + 452 w2 Im s0 25w |
|
2 2 w —w0 |
|
tg j 0 = |
полностью определяющие вынужденные колебания (2.25).
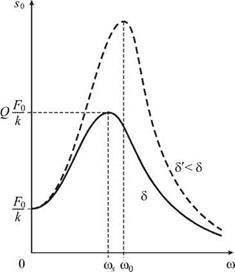
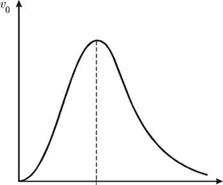
Зависимость амплитуды s0 от частоты w, задаваемая формулой (2.31), называется амплитудно-частотной характеристикой (АЧХ), а зависимость j>0(w), описываемая формулой (2.32), называется фазо-частотной характеристикой (ФЧХ). На рис. 2.3 изображена АЧХ, которая отображает нарастание амплитуды s0 при приближении w к w0. Это явление получило название резонанса смещений. Интересно, что максимальное значение амплитуды, в Q раз превосходящее статическое смещение FJk, достигается на частоте
ws =yjw0 — 252, (2.33)
которая несколько меньше как собственной частоты w0, так и частоты затухающих колебаний - Jw^ — 52 . Для практических целей для частот w, лежащих вблизи частоты w0, формула (2.31) может быть значительно упрощена. Так, можно положить
|
(2.34) |
(w2 — w2)2 = (w0 — w)2(w0 +w)2 » (w0 — w)2 • 4w2;
|
45 2w 2 |
= 45 2w 0.
|
(2.35) (2.36) |
|
+1 |
|
С учетом приближений (2.34) формула (2.31) примет вид: s0(w) = F0 Q - 1 к |
|
V В физике безразмерную функцию L(w) = - |
|
2 w0 — w 5 |
|
2 w0 — w |
|
+1 |
|
5 |
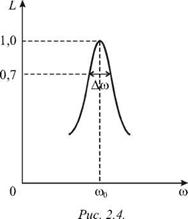
называют лоренцевой, а график этой функции называют лоренцевым контуром. Ширину Aw этого контура, определяющую остроту резонанса, находят из условия убывания
|
|
|
Рис. 2.3. вдвое энергии колебательной системы, пропорциональной квадрату амплитуды s0(w) в (2.35), что эквивалентно приближенному соотношению |
|
|
|
1 |
|
(2.37) |
|
2 |
|
+1 |
|
5 |
|
■ = i » 0,7, V2 |
Aw
которое поясняется рисунком 2.4. При этом условии - q - = 5, т. е. Aw = 25. Ширина лоренцева контура характеризует полосу пропускания колебательной системы, т. е. такую область частот внешней силы, для которых система эффективно откликается на гармоническое внешнее воздействие. Легко видеть, что добротность системы равна
q = _^ = w0
Q 5T Aw’
(2.38)
т. е. обратно пропорциональна полосе пропускания.
С уменьшением коэффициента 5 АЧХ меняет свою форму, как это изображено пунктиром на рис. 2.3 для 5' < 5. Полоса пропускания Aw уменьшается, добротность Q возрастает, и резонанс становится более острым.
|
Рис. 2.5. |
|
|
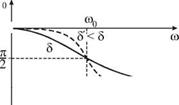
Фазо-частотная характеристика для двух различных коэффициентов затухания изображена на рис. q 2.5. Физическое содержание зависимости j^w) мы подробно обсудили для трех различных режимов вынужденных колебаний. Отметим лишь, что с уменьшением p затухания 5 кривая j^w) становится более «чувствительной» к изменению частоты вблизи резонанса.
Наряду с резонансом смещений можно говорить о резонансе скоростей s и резонансе ускорений s.
Скорость колеблющейся массы равна:
|
(2.39) |
s = s0wsin(wt + j0 + p 2), а ее ускорение:
s' = s0w2 sin(wt + j0 +p), (2.40)
т. е. амплитудно-частотная характеристика для скорости получается умножением АЧХ (2.31) на w, а для ускорения — на w2:
|
v0 = s0w = ■ |
|
2 |
|
/ |
|
22 w2 — w2 w |
|
w0 = s0w = ■ |
|
2 |
|
2 ®0 w2 |
|
5 |
|
- — 1 |
|
+4 |
|
w |
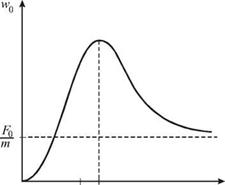
На рис. 2.6 изображены частотные зависимости амплитуд скорости v0 = s0 w и ускорения w0 = s0 w2.
Характерно, что резонанс скорости происходит на частоте ws' = w0 , а резонанс ускорения — при ws" > w0. Отметим, что все резонансные частоты связаны между собой:
ws ■ w^ = w2 = w°. (2.41)
Отметим также, что по причинам, рассмотренным ранее, в области низких частот малы как ускорение, так и скорость. В области высоких частот ускорение конечно (s0w2 ® F0/m) и обеспечивается лишь внешней силой. Однако скорость по-прежнему незначительна, поскольку тело не успевает разогнаться.
Не представляет труда нарисовать самостоятельно фазо-частотные характеристики для скорости и для ускорения, пользуясь формулами (2.39) и (2.40), поскольку они получаются простым сдвигом ФЧХ для смещения (2.32), изображенной на рис. 2.5, вверх соответственно на я/2 или на p.
|
|
|
w0 ws" |
|
w |
В заключение рассмотрим вопрос о подводе энергии к осциллятору при произвольной частоте вынуждающей силы. Средняя за период мощность этой силы равна
|
|
w 0 Рис. 2.6.
|
|
где у 0 = j0 + 2 — сдвиг фаз между скоростью и силой. Мы видим, что максимум подводимой к осциллятору мощности достигается на частоте w0, поскольку при этом максимальны и амплитуда скорости v0, и cos у 0 (у 0 = 0) . При других частотах вынуждающей силы эта мощность быстро уменьшается и стремится к нулю, как при w —— 0, так и при w ® ¥ .
|
|
Баллистический режим колебаний. Рассмотрим колебания системы, к которой приложена произвольная сила F(t), действующая в течение промежутка времени At, значительно меньшего периода собственных колебаний: At << T. Отклик системы на такое воздействие будет пропорционален импульсу действующей силы:
(2.42)
В самом деле, при кратковременном воздействии (в течение времени At) маятник не успевает заметно сместиться из положения равновесия, однако будет обладать ускорением
|
|
(2.43)
m
|
|
При записи (2.43) мы пренебрегли силой вязкого трения. По окончании действия силы маятник приобретет скорость
(2.44)
пропорциональную импульсу силы.
|
(2.45) |
Далее маятник будет совершать собственные гармонические колебания с амплитудой
|
|
w0 mw0
Если параметры m и w0 известны, то можно определить p измеряя амплитуду первого колебания после воздействия.
В качестве примера рассмотрим процедуру измерения заряда, протекающего по электрической цепи, с использованием баллистического гальванометра. Этот гальванометр содержит рамку, которая может совершать крутильные колебания. Рамка имеет увеличенный (по сравнению с обычным гальванометром) момент инерции, что увеличивает период ее собственных колебаний до нескольких секунд. Т. к. рамка находится в магнитном поле постоянного магнита, то при протекании через нее электрического тока на рамку будет действовать момент сил, пропорциональный току. При протекании кратковременного тока рамка приобретает угловую скорость и затем за четверть периода
колебаний отклоняется на некоторый максимальный угол, который пропорционален интегралу от протекшего через рамку тока, т. е. величине протекшего заряда.
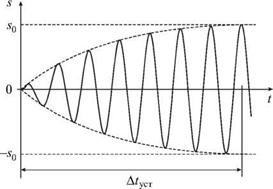
Установление колебаний. Мы уже отмечали, что если приложить к покоящемуся маятнику гармоническую силу в момент времени t = 0, то маятник начнет постепенно раскачиваться, как это качественно изображено на рис. 2.7а. Установление колебаний связано с тем фактом, что наряду с вынужденными колебаниями на частоте w будут возбуждены и собственные колебания на частоте - Jw2 - 52, которые, конечно, будут затухать.
Из математики известно, что общее решение линейного неоднородного уравнения (2.10) при 5 < Wo имеет вид:
s(t) = s0ce-5t sin(^/w2 - 521 + jc) + s0 sin(wt + j0), (2.50)
представляющий собой суперпозицию собственных затухающих колебаний на частоте •Jw2 -52 и незатухающих вынужденных колебаний на частоте W. Из (2.50) видно, что колебания установятся лишь тогда, когда затухнут собственные колебания. Это произойдет по истечении времени
At уст ~ t = 2 (2.51)
5
За это время в систему «закачивается» энергия, поскольку до установления колебаний работа внешней силы превышает работу сил трения. В установившемся режиме имеет место баланс поступающей и расходуемой энергий.
В частности, если w = -jw0 -52 , то (2.50) при s(0) = 0, s(0) = 0 и 5 << w0, как нетрудно показать, имеет вид
s(t) = s0(1 - e-5t )sin(wt - p / 2), (2.52)
p
поскольку при этих условиях s0c = s0, jc = - j0 » —.
|
|
Отметим, что формула (2.51) определяет лишь порядок величины (временной масштаб) At уст. Для практических целей время установления (равно как и время затухания) колебаний принимают равным At уст = (3 + 5)t.
|
|
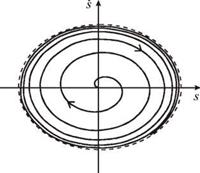
На фазовой плоскости (рис. 2.7б) фазовая траектория будет постепенно «раскручиваться» из начала координат и стремиться к предельному циклу — эллипсу, изображенному на рисунке пунктирной линией.
Характеристики различных колебательных систем (осцилляторов). Интересно сопоставить основные характеристики различных колебательных систем (иногда их для краткости называют осцилляторами) Примерами таких осцилляторов могут быть механические (рассмотренные выше), электрические (известные из школьного курса физики, например, колебательный контур), оптические (например, электрон в атоме) и другие системы.
Вначале обратимся к характеристикам наиболее распространенного осциллятора — маятника, представляющего собой тело, подвешенное на нити.
Маятник является одним из древнейших физических приборов. С помощью крутильных маятников были открыты законы гравитационного и электрического взаимодействий, измерено давление света, выполнено множество других физических экспериментов. В последнее время предложен и реализуется ряд новых экспериментов для изучения фундаментальных свойств материи, в которых очень малые силы измеряются с помощью крутильных маятников. Чувствительность таких экспериментов зависит от того, насколько ослаблены сейсмические возмущения, действующие на маятник, а также от стабильности его параметров, например, упругих свойств нити подвеса. Но даже если устранены все внешние возмущающие воздействия, остается один принципиальный источник флуктуаций его амплитуды и фазы колебаний. Это хаотическое тепловое движение молекул в нити подвеса и подвешенном теле. Действующая на него флуктуационная сила зависит от температуры и от добротности маятника. Чем выше добротность маятника, тем медленнее затухают его колебания и диссипирует его энергия, превращаясь в тепло, т. е. хаотическое движение молекул. Это означает, что ослабевает и обратный процесс раскачки маятника хаотическим движением молекул, т. е. уменьшается флуктуаци - онная сила, действующая на маятник. Для того, чтобы уменьшить затухание, тело и нить подвеса изготовляют из высококачественного плавленого кварца — материала с низкими потерями упругой энергии, а также принимают специальные меры для исключения других источников диссипации энергии. В результате добротность крутильных маятников достигает величины ~107.
В настоящее время в нескольких странах строятся лазерные гравитационные антенны для регистрации гравитационного излучения от космических объектов. Принцип действия антенны основан на том, что гравитационная волна действует на свободные массы, помещенные в разные точки пространства, изменяя расстояние между ними. Это изменение пропорционально интенсивности волны и расстоянию между массами. По этой причине в гравитационных антеннах пробные массы располагают в нескольких километрах друг от друга в специальных вакуумных камерах, а расстояние между ними измеряют уникальным лазерным интерферометром. Каждая пробная масса подвешива-
ется на тонких нитях, образуя маятник качания. С массами связывают два зеркала, отражающие лазерный луч, распространяющийся вдоль прямой, соединяющей эти массы. По сдвигу интерференционной картины, даваемой такой сложной оптической системой, можно «почувствовать» взаимное смещение масс на величину порядка 10-17 см, что на 7 порядков меньше размеров атома! Чувствительность гравитационной антенны ограничена тепловыми флуктуациями колебаний такого маятника, а значит, также определяется его добротностью. В отличие от крутильных, добротность маятников качания зависит не только от потерь в упругом элементе — нити подвеса, но и от ее натяжения. За счет этого эффекта можно значительно увеличить добротность маятника качания. Так, добротность маятников качания, целиком изготовленных из плавленого кварца, может превышать 108, т. е. время затухания их колебаний достигает нескольких лет. Конечно, при столь малой диссипации энергии маятника на его добротность влияют весьма слабые внешние воздействия, например, электрические и магнитные поля, или частицы пыли, осевшие на нити подвеса, и т. д.
При таких высоких значениях добротности и соответствующем подавлении сейсмических возмущений проявляются квантовые свойства маятника. В этом случае поведение вполне макроскопического объекта будет определяться принципом неопределенности Гейзенберга. Правда, необходимые условия реализуются пока для малых временных интервалов (около 10-3 с), и для наблюдения квантовых особенностей поведения маятников требуются очень чувствительные регистрирующие устройства, но именно такие маятники, обладающие предельно высокой добротностью, предполагается использовать в будущих гравитационных антеннах.
Камертон, служащий для настройки музыкальных инструментов, также является высокодобротным осциллятором. Звук, издаваемый вибрирующими ножками камертона, затихает за достаточно длительное время по сравнению с периодом их колебаний. Если, например, собственная частота камертона лежит в диапазоне V = 300 + 400 Гц, а продолжительность звучания (весьма грубо) составляет время порядка t~ 10 с, то камертон совершит Vt ~ 3000 + 4000 колебаний. Это означает, что его добротность по порядку величины равна Q ~ 104.
Как это ни покажется парадоксальным, электрический колебательный контур является менее добротной системой, хотя частота его собственных колебаний имеет по-
5 8
рядок величины V ~ (10 +10 ) Гц. Добротность контура ограничена, главным образом, омическими потерями и имеет порядок величины Q ~ 102. Это, в свою очередь, означает, что полоса пропускания Dv = Q—1 ■ V, введенная ранее при рассмотрении вынужденных колебаний, равна Dv ~ (103 +106) Гц.
Если частота радиопередающей станции Vc высока (vc > 106 Гц), то ее преобразовывают в радиоприемных устройствах до низкой (называемой промежуточной) частоты Vп ~ 105 Гц. Тогда колебательный контур радиоприемника будет иметь очень малую полосу пропускания Dv ~ Q ■ V п ~ 5 ■ 103 Гц. Это значит, что если частоты двух станций V1c
и v 2c соответственно различаются более, чем на величину полосы пропускания (|v1c - v 2с| > Av), то, перестраивая собственную частоту колебательного контура приемника, можно по отдельности настроиться на каждую из этих передающих станций.
Оптический электрон в атоме, осуществляя переходы с одной орбиты на другую, в соответствии с постулатами Бора излучает квант света с энергией hw = E2 - E1. С классической точки зрения это можно интерпретировать таким образом, что электрон совершает колебания на этой частоте w, т. е. является оптическим осциллятором. Поскольку электрон теряет энергию на излучение, то амплитуда его колебаний должна затухать в течение некоторого характерного времени t. Для уединенного атома (не взаимодействующего с соседними атомами) это время определяется зарядом и массой электрона и зависит от частоты w. Однако для всех атомов оно имеет один и тот же порядок величины: t ~ 10-8=10-9 с. Учитывая, что в видимом оптическом диапазоне период колебаний T = 2p/w ~ 10-15 с, легко подсчитать число колебаний до их затухания. Оно имеет порядок
t 6 7
величины т ~ 10 =10 . Поэтому добротность оптического осциллятора (Q ~ 107), будучи высокой, все же уступает добротности прецизионных кварцевых маятников.
|
|
Параметрические колебания. В повседневной жизни мы сталкиваемся с незатухающими колебаниями, для поддержания которых требуется периодически менять какой-либо параметр колебательной системы. Одним из ярких примеров являются колебания качелей. Хорошо известно, что можно поддерживать колебания длительное время, если быстро приседать в момент наибольшего отклонения качелей и также быстро вставать при прохождении положения равновесия. Благодаря этому параметр физического маятника (качелей) — расстояние a между осью вращения и центром масс — меняется скачкообразно на величину ±Aa (Aa << а).Величина Aa должна быть такой, чтобы обеспечить баланс энергии системы: O
потери энергии маятника за период должны компенсироваться за счет рис. 2.8.
совершения работы, осуществляемой при приседании и вставании.
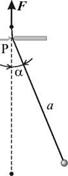
Напишем условие энергетического баланса для простейшего случая колебаний математического маятника с длиной нити а, которая меняется на величину ±Aa (рис. 2.8.). Это можно осуществить, если пропустить нить маятника через отверстие в точке P (точке подвеса) и затем, прикладывая внешнюю силу F к концу нити, периодически менять ее длину.
Рассмотрим установившиеся параметрические колебания маятника с не слишком большими амплитудами и будем считать, что затухание мало (5 << w0). Поскольку Aa << a, то приближенно можно считать, что угол a отклонения маятника от положения равновесия меняется во времени по гармоническому закону
a(t) = a0 sin wt, (2.53)
|
2 1——і 16 |
|
= igi |
|
где согласно (1.42) w » w0 |
|
а w |
|
a. |
|
В момент наибольшего отклонения на угол a0 сила натяжения нити равна N1 = mg cos a0. Поэтому, удлиняя нить на величину Da, внешняя сила F1 = N1 совершает отрицательную работу A-= - mg cos a0 ■D a. Раскладывая cos a0 в ряд |
|
2 4 a 0 a 0 cos a 0 » 1 —— +— +..., получим ( 2 4 ^ a Q a Q A— » —mg 1-------------- 1------- 2 24 При прохождении маятником положения равновесия (a = 0) F2 = N2 = 2 mv0 = mg +---------- , где V0 = a0wa. Поэтому положительная работа при укорачивании нити с |
|
(2.54) |
|
Da. |
|
точностью до членов порядка a0 равна: |
|
a0 |
|
22 A+ = (mg + ma0 w a)Da » mg |
|
1 + a 02 — |
|
(2.55) |
|
Da, |
|
где учтено, что w0 a = g. Полная работа, совершаемая за период внешней силой F, будет положительной и равной |
|
4 A = 2( A+ + A—) = 3mgaQDa-------------------- g—0 Da----- = 3mgaQDa |
|
2 a02 |
|
(2.56) |
|
1— |
|
Потери энергии за период численно равны работе силы трения: T T A^ = J Fтрvdt = ^ Гv2dt, |
|
(2.57) |
|
где F^ = - Гv. |
|
При гармонических колебаниях (2.53) скорость v(t) = a a(t) = aa0w cos wt. Подставляя (2.58) в (2.57) и выполняя интегрирование, получаем: |
|
(2.58) |
|
1—a0 16 |
|
Лір = —Гя 2a 2 w 2 Jcos2wtdt = —ra 2 a J°w 2 — »—ra 2 ga 0 2 X У поскольку wT = w0T0 = 2я. Следовательно, условие баланса энергии состоит в равенстве нулю суммы работ: A + Атр = 0, или |
|
(2.59) |
|
1—aі 1 - 16 V У |
|
3 mga 02 Da |
|
(2.60) |
|
= г—о ga — |
|
Проводя сокращения и используя определение выражение для добротности Q, получаем приближенное выражение для амплитуды a0 установившихся пара- 5T0 метрических колебаний: |
a0 » 2^І1-------------- p . (2.61)
0 3Q( Aa / a)
Отношение Aa/a называют глубиной модуляции параметра a. Из (2.61) видно, что для возникновения параметрических колебаний глубина модуляции должна превзойти некоторое минимальное (пороговое) значение, примерно равное величине, обратной добротности:
— > -1. (2.62)
a Q
Чем более добротна система, тем меньше пороговая глубина модуляции. С повышением величины Aa/a амплитуда колебаний a0, как это следует из формулы (2.61), будет увеличиваться. Однако при больших амплитудах (a0 > 1) формула (2.61) становится мало приемлемой, поскольку сделанные нами приближения становятся неприменимыми.
Следует отметить, что параметрическое возбуждение является существенно нелинейным эффектом. Это видно, в частности, из уравнения (2.60): если пренебречь в нем малыми слагаемыми ~ a2, которые описывают нелинейность, то a0 из уравнения
Aa Р А
выпадает, и получается соотношение — = — . Физически это означает, что при таком
a 3Q
значении глубины модуляции энергетический баланс в системе обеспечивается при любых амплитудах a0, что неверно.
Заметим, что возбуждение параметрических колебаний, вообще говоря, может происходить не только на удвоенной частоте собственных колебаний системы, когда параметр меняется один раз за каждые полпериода, но и при более редком воздействии: через один, два, три и т. д. полупериодов колебаний, т. е. на частотах 2w0/n, где n — любое целое число. Возбуждение также возможно внутри некоторой области — вблизи каждой из этих частот, но пороговые значения глубины модуляции для разных частот будут различны.
Автоколебания. Наблюдая колебания листьев деревьев, дорожных знаков над проезжей частью улиц, полотнищ на ветру и др., мы понимаем, что во всех перечисленных случаях незатухающие колебания происходят за счет энергии постоянно дующего ветра. При этом сама колебательная система производит отбор энергии ветра в нужный момент времени и в количестве, требуемом для компенсации неизбежно присутствующих энергетических потерь. Колебания в этих системах начинаются самопроизвольно за счет начальных флуктуаций (дрожаний) колеблющихся предметов. Частота и амплитуда установившихся колебаний определяется как параметрами самой системы, так и параметрами ее взаимодействия с ветром. Такие колебания являются примерами автоколебаний, а сами системы — примерами автоколебательных систем.
|
|
|
|
Классическим примером автоколебательной системы служат механические часы с маятником и гирями. Эти часы периодически «черпают» энергию при опускании гирь, подвешенных к цепочке, перекинутой через шестерню часового механизма.
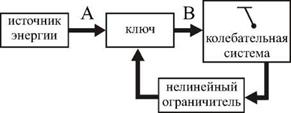
Принцип работы всех автоколебательных систем можно понять, обратившись к схеме, изображенной на рис. 2.9а.
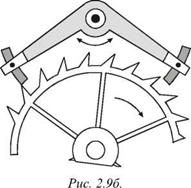
Периодическим поступлением энергии в колебательную систему от источника энергии по каналу АВ управляет сама колебательная система посредством обратной связи. Схематически это изображено в виде некоторого запирающего канал АВ устройства (ключа), который управляется самой системой. Так, в зависимости от положения и скорости колеблющегося листа на ветру будет различной мощность сил аэродинамического давления. В конструкции часового механизма (рис. 2.9б) присутствует специальное устройство — анкер, выполняющий роль ключа. Этот анкер, представляющий собой коромысло, приводится в колебание самим маятником часов. При определенных положениях он «отпирает» одну из шестерен часового механизма. В этот момент времени шестерня проворачивается за счет момента сил, приложенного со стороны натянутой цепи с грузом. Груз при этом опускается на небольшую величину. Количество энергии, поступающей в часовой механизм, равно по величине уменьшению потенциальной энергии груза в поле силы тяжести.
Важно отметить, что любая автоколебательная система нелинейна. На схеме это отражено наличием в системе обратной связи нелинейного ограничителя сигнала, управляющего ключом. Нелинейность системы проявляется в том, что при начальном нарастании амплитуды колебаний, порожденных флуктуациями, поступление энергии в систему за каждый последующий период колебаний увеличивается нелинейно, т. е. прирост поступающей энергии становится все меньше и меньше. Естественно, что амплитуда колебаний достигнет такой установившейся величины, при которой приток энергии и ее потери будут равны по величине.
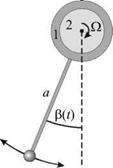
Маятник на вращающемся валу (маятник Фруца). Для более углубленного изучения принципа действия автоколебательной системы проанализируем колебания маятника, подвес которого скреплен с муфтой 1, одетой на горизонтальный вал 2 (рис. 2.10).
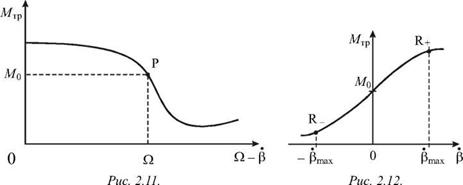
Пусть вал вращается с постоянной угловой скоростью W по часовой стрелке. Если угол отклонения маятника от вертикали b(t) меняется с течением времени, то сила сухого трения в подвесе, нелинейно зависящая от относительной скорости муфты и вала W - р, также будет меняться во времени (р — угловая скорость муфты). Момент этой силы Мтр будет оказывать периодическое воздействие на маятник, поддерживая его колебания. На рис. 2.11 изображена нелинейная зависимость Мтр от относительной угловой скорости муфты и вала. На изображенной кривой имеется точка перегиба P. Подберем скорость вращения вала W такой, чтобы в
|
|
отсутствие колебаний (р = 0) попасть в эту точку. В этом случае к муфте маятника будет
приложен постоянный момент силы трения: Мтр = M,. Для дальнейшего анализа более удобно воспользоваться зависимостью Мтр( р), изображенной на рис. 2.12. Следует подчеркнуть, что начальное (линейное) нарастание Мтр с угловой скоростью р обеспечивает условие для самопроизвольного нарастания колебаний из флуктуации, что эквивалентно наличию положительной обратной связи, а последующее замедление роста Мтр при увеличении р& является причиной нелинейного ограничения нарастания колебаний: амплитуда смещения маятника (а значит и амплитуда его скорости рmax ) достигнет максимальной (установившейся) величины, что эквивалентно наличию нелинейного ограничителя.
Отклоним осторожно маятник от вертикали на угол ро такой, чтобы момент силы трения, действующий на неподвижный маятник, Mo = M (0), был уравновешен моментом силы тяжести Мфо) = mga sin ро:
М тр(0) = М (ро), или М 0 = mga sin ро. (2.63)
Здесь m — масса маятника, а — расстояние от вала до центра масс маятника.
На первый взгляд, может показаться, что маятник так и останется висеть под углом ро к вертикали. На самом деле это положение будет неустойчивым. Представим, что в результате ничтожного толчка маятник приобретет небольшую угловую скорость
|
|
b > 0. При этом возрастут моменты сил тяжести Ми трения Мтр , и условие (2.63) может нарушиться. Если начальный наклон кривой Мтр( р ) на рис. 2.12 достаточно велик (сильная положительная обратная связь), то Мтр( р) > М (Р0). Это означает, что угловая скорость р будет нарастать. Однако затем это нарастание прекратится, т. к. из-за нелинейного загиба кривой Мтр( р ) равенство моментов опять восстановится (сработает механизм нелинейного ограничения):
Мтр (bmax ) = М(р). (2.64)
Условию (2.64) соответствует точка R+ на кривой Мтр( р). После этого угловая скорость начнет уменьшаться, поскольку с ростом угла р момент М(р) продолжает расти, а Мтр( р) — убывать. Следовательно, маятник спустя какое-то время остановится, а его угол отклонения достигнет максимальной величины ртах. Поскольку в этот момент М(ртах) > Мтр = М0, то маятник начнет двигаться в обратном направлении. Момент силы тяжести начнет уменьшаться, а момент силы трения будет также уменьшаться, но быстрее, чем момент силы тяжести (опять срабатывает положительная обратная связь). Сначала это движение будет ускоренным, пока М > Мтр (до точки R - на рис. 2.12), а затем при М < Мтр — замедленным (до точки P на рис. 2.12). Остановившись при некотором угле наклона ртіп, маятник опять движется влево, т. к. все еще М < Мтр. Наконец, он достигает стартовой позиции, однако приобретенная им скорость будет больше скорости начального толчка. Таким образом, в течение одного периода колебаний увеличилась энергия маятника за счет ее заимствования от устройства, вращающего вал.
В последующие периоды колебаний точки R+ и R - на кривой М тр (р) будут сдвигаться в разные стороны, однако из-за нелинейности кривой этот сдвиг прекратится (срабатывает механизм нелинейного ограничения), и колебания установятся.
Чтобы количественно проанализировать автоколебания маятника, запишем уравнение вращательного движения маятника с моментом инерции J:
ір = Мтр(р) — mga sin р. (2.65)
В этом уравнении мы пока пренебрежем моментом силы вязкого трения, действующей на движущийся маятник. Момент силы сухого трения в подвесе, нелинейно зависящий от угловой скорости р (см. рис. 2.12), можно аппроксимировать следующим выражением
М тр(р) = М 0 + к1р — кор3, (2.66)
где k1 и k2 — размерные коэффициенты, определяющие обратную связь и нелинейное ограничение соответственно. Если колебание описывать углом отклонения a от положения неустойчивого равновесия, задаваемого углом р0 (— = р — р0), то
mga sin р = mga(sin р0 cos a + cosр0 sin a). (2.67)
Для малых углов cos a» 1, sin a»a. Если учесть далее, что р = a, то уравнение (2.65) примет вид:
j— + mga cos р0а = kja — k0 a3. (2.68)
Это уравнение является нелинейным дифференциальным уравнением и не имеет аналитического решения. В теории колебаний развиты методы, позволяющие решить его приближенно, исследовать условия, при которых возможно самовозбуждение колебаний, и найти амплитуду —0 и частоту w установившихся колебаний:
a(t) = a0 sin wt. (2.69)
Мы же поступим более просто и определим a0 из условия энергетического баланса. Поскольку правая часть (2.68) мала, то частота колебаний приближенно равна: mga cosр0/ J.
Подсчитаем работу за период колебаний Т = 2pw, совершаемую устройством (например, электродвигателем), вращающим вал. Она, очевидно, равна:
т
A = J Мтр (р)Щ/ = М0ОТ. (2.70)
0
Здесь учтено, что интегралы по времени от р и р3 равны нулю, поскольку
р = — = a0 wcos wt. (2.71)
Потери энергии в скользящем подвесе за это время составят величину
|
2^2 |
|
4,-4 |
|
k1a 0ю |
|
3k2a0w |
|
q = J Мтр(р)(0 — 0)dt = |
|
М 0W — |
|
(2.72) |
|
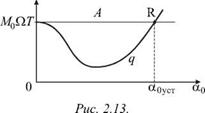
На рис. 2.13 изображены зависимости A и q от амплитуды a0. Видно, что при случайных флуктуациях, когда —0 мало, A > q. Это означает, что колебания будут нарастать. Однако с ростом амплитуды начинают расти потери q. Колебания установятся при A = q (точка R на графике). Амплитуда установившихся колебаний определится из равенства |
|
|
|
44 3k 0 a 0уст Ю |
|
kja |
|
w |
|
0уст |
|
М 0WT = М 0WT — |
|
(2.73) |
|
Отсюда |
|
1 |
|
a |
|
(2.74) |
|
0 уст |
|
w v 3k |
|
2 |
|
Заметим, что теперь мы можем легко учесть силы вязкого трения, для чего в правую часть уравнения (2.68) следует добавить член —Г— . Это приведет к тому, что ^ в (2.74) будет уменьшен на величину Г. Поэтому (2.74) изменится: і |
|
kj —Г 3k0 . |
|
a |
|
(2.75) |
|
0 уст |
|
Из последнего выражения следует, что при Г> kl колебания не могут самопроизвольно начаться. |
Автоколебательные системы находят широчайшее применение в технике. Так, например, духовые и смычковые инструменты, органные трубы, генераторы электромагнитного излучения в приемно-передающих линиях связи, оптические квантовые генераторы (лазеры) и др. представляют примеры автоколебательных систем.
Однако, автоколебания могут играть и негативную роль, начиная от безобидных колебаний деталей кранов водопроводных систем, «ревущих» при достаточном напоре воды, до опасных колебаний крыльев самолетов, получивших название «флаттер». В ноябре 1940 г. подвесной мост через реку Такома в США разрушился из-за крутильных автоколебаний, возникших под действием дувшего вдоль реки ветра.

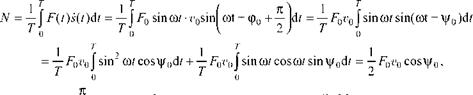
 Опубликовано в
Опубликовано в