Расширение автоматизации производства, развитие дистанцион­ного контроля и регулирования требуют создания информационно­измерительных систем, осуществляющих управление сложными тех­нологическими процессами по многим параметрам, передачу инфор­мации по каналам связи, а также быструю и надежную ее обработ­ку. В связи с этим особую актуальность приобретают устройства, выдающие информацию об измеряемых величинах в дискретной форме, например в виде частоты переменного тока или напряжения, числа импульсов в единицу времени или конечных интервалов вре­мени. Такую информацию удобно передавать на расстояние и можно непосредственно вводить в электронно-вычислительные машины.

Преимущества цифровых измерительных устройств могут быть реализованы только в том случае, если функция преобразования входной величины является линейной. Коррекция нелинейности вы­ходной характеристики таких устройств осуществляется обычно (пу­тем введения в их электронные схемы специальных функциональных элементов, что приводит подчас к значительному усложнению устройств. В целом же такие преобразователи нелинейны, и только ограниченные участки их выходных характеристик можно аппрокси­мировать прямыми. При использовании индуктивно-частотных преоб­разователей в качестве входных устройств приборов с дискретным выходом представляется возможность линеаризации их выходной ха­рактеристики более простым способом: за счет выбора специального первичного элемента.

В вычислительной технике используются магнитные элементы с (Профилированной намоткой с целью получения необходимой функ­циональной зависимости от перемещения. Примером могут служить трансформаторы с магнитной коммутацией как функциональные пре­образователи для реализации различных математических зависимо­стей. В некоторых вариантах этих приборов используется принцип построения функциональных элементов с помощью профилирования обмотки {Л. 21]. Такие преобразователи выдают напряжение в опре­деленной функции от перемещения. Нужный вид зависимости полу­чается за счет магнитной коммутации витков обмоток, расположен­ных на магнитопроводе. Параметры единицы длины обмоток неоди­наковы и обусловлены заданным функциональным преобразованием. Положение коммутирующего элемента (магнитного или электриче­ского) определяет рабочий участок преобразователя. Именно на этом участке замыкается рабочий поток; остальная часть обмотки в работе не участвует. При этом общий магнитный поток остается неизменным, а изменяется лишь число потокосцеплений в зависимо­сти от положения коммутатора. Для подобных систем характерно наличие замкнутой магнитной цепи. На том же принципе основаны потенциометрические функциональные преобразователи. В них 'при неизменном токе необходимая зависимость реализуется за счет изме­нения падения напряжения на единицу длины, что достигается про­филированием обмотки, причем в преобразовании участвует только часть витков до электрического коммутирующего элемента.

Принципиальное отличие функционального преобразователя на основе индуктивно-частотного преобразователя заключается в том, что в нем отсутствует коммутация витков обмотки первичного эле­мента при перемещении сердечника. В измерительную схему обмотка всегда включена полностью, замкнутая магнитная цепь отсутствует, и при движении сердечника меняются по необходимому закону об­щая картина поля и индуктивность всей катушки.

Следует иметь в виду, что в случае линейного частотного пре­образователя достаточно малых перемещений с миниатюрным пер­вичным элементом, длина которого соизмерима с измеряемыми пе­ремещениями (/=3-^5 мм), применение методов функционального преобразования с коммутирующими элементами теряет смысл. Не­обходимая для указанного метода замкнутая магнитная цепь не может быть осуществлена ввиду того, что резко неравномерное рас­пределение витков на магнитопроводе сделало бы воздушный зазор соизмеримым с длиной магнитопровода первичного преобразователя.

Рассмотрим индуктивно-частотный преобразователь с дискрет­ным выходом, имеющий первичпый элемент, который выполняет функции корректора нелинейной характеристики. В предыдущих раз­делах указывалось, что индуктивно-частотный преобразователь пред­ставляет собой управляемый генератор электрических колебаний, в задающий контур которого включена катушка индуктивности дат­чика. Как явствует из соотношения (1-4), между частотой и индук­тивностью существует нелинейная зависимость. Вводя обозначение

Для получения на выходе индуктивно-частогного преобразователя изменений частоты, прямо пропорциональных входным перемеще­ниям, необходимо обеспечить такую характеристику первичного пре­образователя, которая скомпенсировала бы нелинейность зависимо­сти (4-1) на значительном участке.

Попытки использования для этой цели датчика с Ш-образным сердечником и >с переменным воздушным зазором [Л. 20] не позво­лили получить удовлетворительной линеаризации выходной харак­теристики даже на участке в 50 мк. При использовании в качестве первичных элементов катушек индуктивности с разомкнутой магнит­ной цепью и с подвижным сердечником, перемещающимся внутри катушки вдоль ее оси, поставленная задача успешно решается на значительно большем участке перемещений сердечника.

Несмотря на приближенный характер, приведенные соотноше­ния хорошо отражают качественную сторону вопроса, показывают принципиальную возможность линеаризации характеристики индук - тивно-частотного преобразователя и способ ее осуществления — обе­спечение соответствующего закона изменения индуктивности катуш­ки датчика при движении ферритового сердечника.

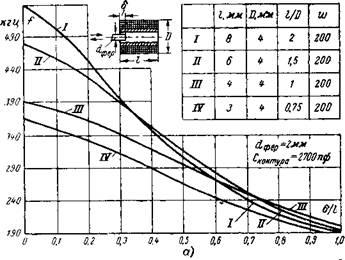
На рис. 4-1,а показаны построенные в относительных единицах экспериментальные характеристики преобразователя с цилиндри­ческими катушками индуктивности. Катушки отличаются отноше­нием длины к диаметру при постоянном числе витков. Приведен­ные графики подтверждают теоретический ход кривой /(б) и пока­зывают также, что с увеличением длины катушки растет кривизна характеристики преобразователя.

Экспериментальные исследования показали, что наиболее эф­фективным является использование в качестве первичного элемента коротких катушек с отношением длины к диаметру, близким к еди­нице: /к/^к = 0,8ч-1,1. Найдены средства, позволяющие в несколько раз расширить величину линейного участка характеристики преоб­разователей с такими катушками (Л. 34].

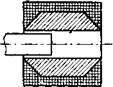
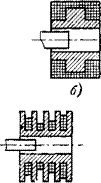
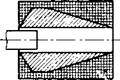
Из рассмотрения графиков рис. 4-1,а» видно, что для коррекции нелинейности характеристики /(б) необходимо обеспечить усиление поля на краях катушки или, наоборот, ослабление в средней ее части. Это достигается изготовлением катушек с переменным числом витков на единицу длины. Конструкция катушек без профилирования показана на рись 4-2,а. На рис. 4-2,6 показаны катушки с внутрен­ним профилированием за счет использования специальных немаг­нитных каркасов. В этом случае наблюдается понижение чувстви­тельности преобразователя ввиду удаления части витков катушек от сердечника. В случае наружного профилирования (рис. 4-2,в) коррекция достигается без потери чувствительности. Усиления поля на торцах катушки можно добиться также при использовании фер- ритовых колец (рис. 4-2,г). Все перечисленные виды коррекции мо­гут применяться на практике.

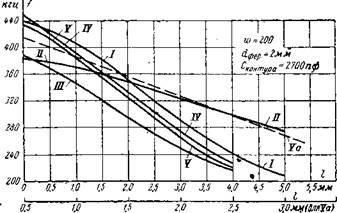
На рис. 4-1,6 приведены линеаризованные характеристики пре­образователя с различными конструкциями первичных элементов. Измерения проводились при помощи цифрового частотомера ЧЗ-З с интервалами 5, 10, а в ряде случаев 1 и 2 мк. Оценим получен­ные характеристики с точки зрения их линейности и чувствитель­ности прибора.

/ — характеристика преобразователя с катушкой первичного элемента без коррекции (рис. 4-2, а). Линейный участок ее относи­тельно невелик и составляет 20% от длины намотки.

II — характеристика преобразователя с катушкой с внутренним профилированием (рис. 4-2,6). Как видно из сравнения с другими характеристиками, чувствительность в этом случае снижается более чем в 2 раза (v = 25 гц/мк в пределах линейного участка). Линейный участок составляет 50% длины катушки.

III — характеристика катушки с тремя секциями (рис. 4-2,в). Линейный участок составляет 37% от длины катушки; v = 60 гц/мк.

IV, V — характеристики четырехсекционных катушек, имеющих различные распределения обмоток в секции (рис. 4-2,в). Линейные участки составляют 40 и 50% при чувствительности v«70 гц/мк.

Va — построенный в увеличенном масштабе линейный участок характеристики V. Нелинейность характеристик преобразователей с датчиками, имеющими профилированную намотку, лежит в пре­делах 0,7—0,8% на участке перемещений сердечника до 70% от дли­ны катушки и порядка 0,1—0,2% при участке перемещения до 30% от длины катушки.

Абсолютная чувствительность преобразователя v = A//A/ зависит от выбора рабочего частотного диапазона и растет при смещении его в область более высоких частот. Выбор частотного диапазона определяется необходимостью получения нужной чувствительности, габаритами первичного преобразователя и конкретными требования­ми эксплуатации.

Экспериментальные исследования дрейфа частоты генератора, показанного на рис. 1-£, с помощью цифрового частотомера показа­ли, что относительный уход частоты в течение часа составляет 4. 10~4, минутный уход равен 5 - 10—6. Это соответствует теорети­ческой разрешающей способности ин­дуктивно-частотного преобразователя (при имеющейся чувствительности) порядка десятых долей микрона.

Устройства с дискретным выхо­дом на основе индуктивно-частотных преобразователей имеют преимуще­ства перед другими устройствами, в которых частота на определенных участках является линейной функ­цией одного из электрических пара­метров схемы (например, Д или С).

Дело в том, что наиболее универ­сальным параметром, в который пре­образуется большинство измеряемых неэлектрических величин, является перемещение. Поэтому в указан­ных преобразователях необходимо обеспечить также и линейную зависимость между перемещениями, в которые преобразуется изме­ряемая величина, и одним из электрических параметров схемы преобразователя.

Для сокращения объема передаваемой на расстояние информа­ции и для обеспечения ввода ее в цифровые электронно-вычислитель­ные машины могут быть использованы дифференциальные схемы преобразователей. В таких преобразователях (рис. 4-3) катушки датчика включаются в задающие контуры двух идентичных генера­торов 1 и 2, сигналы которых подаются на смеситель 3, на выходе которого получается частота, равная разности частот генераторов. Эта частота фиксируется счетчиком 4. При нулевом или начальном значении измеряемой величины сигнал на выходе отсутствует, а при ее изменениях становится равным:

(fo+Af)— (/о — Д/) = 2Д/.

Такая схема обеспечивает большую линейность и позволяет отсчитывать абсолютное значение измеряемой величины.