Carrier loss in double heterostructures
 10 марта, 2014
10 марта, 2014  admin
admin In an ideal LED, the injected carriers are confined to the active region by the barrier layers adjoining the active regions. By means of confinement of carriers to the active region, a high carrier concentration is attained resulting in a high radiative efficiency of the recombination process.
The energy barriers confining the carriers to the active region are typically of the order of several hundred meV, i. e. much larger than kT. Nevertheless, some carriers will succeed in escaping from the active region into the barrier layers. The concentration of the escaping carriers in the barrier layers will be rather low, resulting in a low radiative efficiency of carriers in the barrier layers.
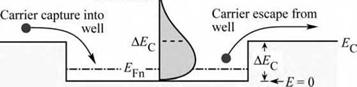
Free carriers in the active region are distributed according to the Fermi-Dirac distribution and, as a result, some carriers have a higher energy than the height of the confining barrier. Thus some of the carriers escape from the active region into the barrier regions as illustrated in
|
Carrier distribution
Ж ДEyj _L_ |
Fig. 4.11.
Fig. 4.11. Carrier capture and escape in a double heterostructure. Also shown is the carrier distribution in the active layer.
Consider electrons in the active region of a double heterostructure and assume that the active region is clad by a barrier with height AEC, as shown in Fig. 4.11. The energy distribution of
carriers is given by the Fermi-Dirac distribution. Thus, a certain fraction of the carriers residing in the active region have an energy higher than the energy of the barrier. The concentration of electrons with energy higher than the barrier is given by
p <X
|
(4.23) |
nB = J E pDOS fFD(E)dE
where pDOS is the density of states, fFD is the Fermi-Dirac distribution function, and EB is the height of the barrier. For a bulk-type density of states, the concentration of carriers with energy higher than EB is given by
|
Г л3/2 1 2 m* ' |
|
■x/E-E |
|
1 |
|
Л <X J Eb 1 |
|
dE. |
|
(4.24) |
|
nB = |
|
(E - EFn)/ kT |
|
2П |
|
+ e |
Taking into account that we are interested in carriers with energies much higher than the Fermi energy, the Fermi-Dirac distribution can be approximated by the Boltzmann distribution. One obtains
|
(4.25) |
|
nB |
= Nc e (EFn - EB ) / kT
where Nc is the effective density of states in the active region. Equation (4.25) gives the concentration of free carriers at the active-region-cladding-region interface. Minority carriers at the edge of the cladding layer will diffuse into the cladding layer. The diffusion process is governed by the initial concentration nB and the electron diffusion length Ln. Taking the location of the origin (x = 0) at the edge of the barrier, the carrier distribution can be written as
|
- (EB - EFn)/ kT e-x / Ln |
|
(4.26) |
|
= Nc e |
|
nB(x) = nB(0)e x / Ln |
where Ln = (Dn Tn)12 is the diffusion length, Tn is the minority carrier lifetime, and Dn is the diffusion constant. The diffusion constant can be inferred from the mobility using the Einstein relation D = p kT / e.
The diffusion current density of electrons leaking over the barrier can be obtained from the carrier concentration gradient at x = 0, i. e.
|
dnB( x) dx |
|
nB(0) Ln |
|
= - e Dn |
|
(4.27) |
|
j = - eD Jnx=0 |
The leakage current depends on the carrier concentration at the edge of the barrier. Thus a high barrier height is required to minimize the leakage current. Clearly, barriers must be much larger than kT for efficient confinement of carriers. Some material systems such as AlGaN/GaN or AlGaAs/GaAs have relatively high barriers and therefore lower leakage currents over the barrier. Other material systems such as AlGalnP/AlGalnP emitting at 600-650 nm have lower barriers and therefore have a stronger carrier leakage over the barriers.
Note that the leakage increases exponentially with temperature. Thus, a decrease of the radiative efficiency of LEDs results as the temperature increases. To reduce the temperature dependence of the emission, high barriers are required. In addition to carrier leakage, other effects, such as Shockley-Read recombination also contribute to the lower radiative efficiency at high temperatures.
Exercise: Carrier leakage over a barrier. Electrons in the active region of a GaAs structure have a concentration of 2 x 1018 cm-3. Calculate the current density of the carrier loss over the barrier for barrier heights of 200 and 300 meV, assuming an electron mobility of 2000 cm2/(V s) and a minority carrier lifetime of 5 ns. Compare the calculated leakage current to LED injection currents of 0.1-1.0 kA/cm2.
Solution: The Fermi level in GaAs with electron density of 2 x 1018 cm-3 is 77 meV above the conduction band edge. Assuming that the effective density of states in the barrier is the same as in the GaAs active region, the carrier concentrations at the edge of the barrier are 3.9 x 1015 cm-3 for a 200 meV barrier and 8.3 x 1013 cm-3 for a 300 meV barrier. The diffusion constant, as inferred from the Einstein relation, is Dn = 51.7 cm2/s. The diffusion length is then given by Ln = (Dn Tn)12 = 5.1 ^m. The leakage current is calculated using Eq. (4.27), and one obtains 63 A/cm2 for the 200 meV barrier and 1.3 A/cm2 for the 300 meV barrier. Comparison with diode current densities of 0.1-1.0 kA/cm2 suggests that leakage currents can be a significant loss mechanism, particularly for small barrier heights.
In the consideration above, we have assumed that electrons diffuse in the p-type region and have neglected any drift. However, if the p-type region has a substantial resistance, electron drift cannot be neglected. This drift will enhance the electron current. Furthermore, electrical contacts have been neglected. The minority carrier concentration at the contact-semiconductor interface can be assumed to be zero due to the high surface recombination velocity of such interfaces. Taking these effects into account, the leakage current was calculated by Ebeling (1993). If the distance of the contact from the active-barrier interface is denoted by xp, the leakage current is given by
|
11 — + |
|
1 |
|
1 |
|
1 |
|
Jn _ e Dn nB(0) |
|
coth |
|
(4.28) |
|
+ |
|
l2 Lnf |
|
L2 r |
|
L2 Lnf |
|
nf |
where
Lf = , (4.29)
e Jtot
ap is the conductivity of the p-type cladding region, and Jtot is the total diode current density.
4.4 Carrier overflow in double heterostructures The overflow of carriers from the active region into the confinement regions is another loss mechanism. Carrier overflow occurs at high injection current densities. As the injection current increases, the carrier concentration in the active region increases and the Fermi energy rises. For sufficiently high current densities, the Fermi energy will rise to the top of the barrier. The active region is flooded with carriers and a further increase in injection current density will not increase the carrier concentration in the active region. As a result, the optical intensity saturates. At high injection current densities, carrier overflow occurs, even if the barriers are sufficiently high, so that carrier leakage over the barriers at low injection current densities can be neglected.
|
(a) |
|
Fig. 4.12. Fermi level (£pn) and subband level (£0) in (a) a double heterostructure and (b) a quantum well structure. |
|
A£vl |
|
IV, |
|
1 n r? —► |
j І |
|
|
Fn Д£ |
||
|
і - £ = 0 * |
|
AE, |
|
(b) |
|
■ £Fn -£o -£ = 0 |
|
A£vf |
|
DH |
Consider a double heterostructure LED with an active region of thickness WDH, as shown in
Fig. 4.12. The rate equation of carrier supply to (by injection) and removal from (by
recombination) the active region is given by
dn J r, ґл
- Bnp, (4.30)
|
DH |
dt eWD
|
eBWDH |
where B is the bimolecular recombination coefficient. For high injection densities, it is n = p. Solving Eq. (4.30) for n under steady-state conditions (dn / dt = 0), yields
The carrier density increases with the current injected into the device. As a result, the Fermi energy rises. In the high-density approximation, the Fermi energy is given by
|
. О I'і
|
(4.32)
|
|
|
J overflow |
At high injection levels, the Fermi energy rises and will eventually reach the top of the barrier. At that point, it is EF - EC = AEC. Using this value, the current density at which the active region overflows can be calculated from Eqs. (4.31) and (4.32) and one obtains
(4.33)
Either the conduction band or the valence band well may overflow first depending on the effective density of states (Nc, Nv) and the band discontinuities (AEC, AEV).
Exercise: Carrier overflow in a double heterostructure. Consider electrons in a GaAs double heterostructure with a barrier height of AEC = 200 meV and an active region thickness of WDH = 500 A. Calculate the current level at which the electron well overflows.
Solution: Using Nc = 4.4 x 1017 cm-3 and B = 10-10 cm3/s, one obtains from Eq. (4.33) a current level
Generally, the problem of carrier overflow is more severe in structures with a small active- region volume. In particular, single-quantum-well structures and quantum-dot active regions have an inherently small volume. At a certain current density, the active region is filled with carriers, and the injection of additional carriers will not lead to an increase in the emitted light intensity.
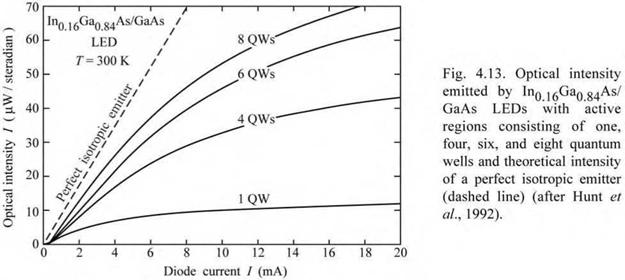
Experimental results of an LED structure with one, four, six, and eight quantum wells (QWs) are shown in Fig. 4.13 (Hunt et al., 1992). The light intensity for the single QW structure saturates at a low current level. As the number of quantum wells is increased, the current level at which saturation occurs increases, and the optical saturation intensity increases as well. The saturation of the light intensity displayed in Fig. 4.13 is caused by the overflow of carriers.
The calculation of the overflow current level is different for quantum well structures and bulk active regions. For quantum well structures, we must employ the two-dimensional (2D) density of states, rather than the 3D density of states that was used in the above calculation. The Fermi
|
level in a QW with one quantized state with energy E0 is given by |
|
( п^_Л vNc2D |
|
EF - E0 kT |
|
(4.34) |
|
- ln |
|
-1 |
|
exp |
|
2D 2 2D where n is the 2D carrier density per cm and Nc is the effective 2D density of states given by |
|
m • |
|
2D |
|
kT |
|
(4.35) |
|
N |
|
Because we are dealing with high carrier densities, the high-degeneracy approximation can be employed and one obtains |
|
П h 2D n |
|
(4.36) |
|
EF - E0 - |
|
m • |
|
|
|
Next, we write the rate equation for the quantum well. The rate equation of carrier supply to (by injection) and removal from (by recombination) the active region is given by |
|
2D |
|
dn |
|
J - B2D n2D p2D e |
|
(4.37) |
|
dt |
|
2D where B « B/ WqW is the bimolecular recombination coefficient for a 2D structure. For high |
injection densities, it is n2D = p2D. Solving Eq. (4.37) for n2D under steady-state conditions
(dn2D / dt = 0), yields
|
JWQ |
|
J |
|
QW |
|
2D |
|
n |
|
і |
|
2D |
|
eB |
|
eB |
|
(4.38) |
|
|
At high injection levels, the Fermi energy will reach the top of the barrier. At that point, EF - E0 = AEC - E0 . The use of this value in Eq. (4.36) and subsequent elimination of n2D from Eqs. (4.36) and (4.38) yields the current density at which the active region overflows
(4.39)
Thus overflow of the active region is a potential problem in double heterostructures as well as quantum well structures. In order to avoid this problem, high-current LEDs must employ thick double heterostructure active regions, or many QWs of multiple QW (MQW) active regions, or a large injection (contact) area. By choosing these parameters, the volume of the active region can be designed in such a way that at the intended current density of operation, carrier overflow does not occur.
4.5 Electron-blocking layers Carriers tend to escape from the active layer of an LED into the confinement layers. The carrier escape can be substantial in double heterostructures with a low barrier height at the active - confinement interface. In addition, high temperatures promote carrier loss out of the active region due to the increase in carrier thermal energy.
The electron leakage current is larger than the hole leakage current due to the usually larger diffusion constant of electrons compared with holes in III-V semiconductors. To reduce carrier leakage out of the active region, carrier-blocking layers are used. In particular, electron-blocking layers or electron blockers are used in many LED structures to reduce electron escape out of the active region. Such electron-blocking layers are regions with a high bandgap energy located at the confinement-active interface.
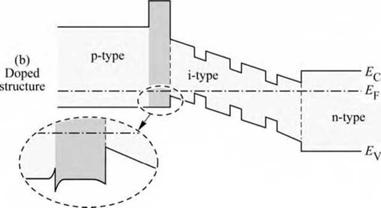
The band diagram of a GaInN LED with an electron-blocking layer is shown in Fig. 4.14. The LED has AlGaN confinement layers and a GaInN/GaN multiple quantum well active region. An AlGaN electron-blocking layer is included in the p-type confinement layer at the
confinement-active interface. Figure 4.14 (a), showing the undoped structure, illustrates that the AlGaN electron-blocking layer creates a barrier to current flow in both the conduction band as well as the valence band.
However, Fig. 4.14 (b), showing the doped structure, illustrates that the barrier in the valence band is screened by free carriers so that there is no barrier to the flow of holes in the p-type confinement layer. That is, the entire band discontinuity is located in the conduction band, i. e.
barrier height for electrons = ^confinement - ^Qactive + AEg (4 40)
where AEg is the difference in bandgap energy between the confinement and the electron - blocking layer.
|
Confinement l-lectron- layer blocking mqw layer active region A------------------- |
|
Confinement layer ,—*—- I-------- *c- |
|
r |
|
1 |
|
U LJ LT |
|
(a) |
|
Undoped -------------------------------------------------------------------------------------------------------------- £----- - structure Г1ГП—П- |
|
Fig. 4.14. AlGaN electron- blocking layer in an AlGaN/ GaN/GalnN multi-quantum well structure, (a) Band diagram without doping, (b) Band diagram with doping. The Al content in the electron-blocking layer is higher than in the p-type confinement layer. |
|
Ev~ |
|
|
|
AlGaN |
|
LaІП |
|
AIGaN |
|
'-GaInN — GaN |
|
L—AlGaN |
The inset of Fig. 4.14 shows the valence band edge of the electron-blocking layer in greater detail. A potential spike (hole depletion layer in the electron blocker) and notch (hole accumulation layer in the p-type confinement layer) occur at the confinement-blocking layer interface. Holes must tunnel through the potential spike when propagating towards the active region. Note that the valence band edge can be completely smoothed out by compositional
grading at the confinement-blocking layer interface so that the electron blocking layer does not impede the hole flow at all.

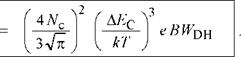
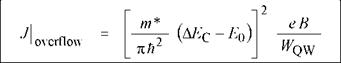
 Опубликовано в
Опубликовано в