При сложной форме зоны разрушения упругую податливость поля собственных напряжений Al0 можно вычислить по схеме рис. 7.14, только решая плоскую задачу теории упругости числен­ными методами. Однако если при вычислении Al0 заменить дейст­вительную зону разрушения фиктивной трещиной, распространен­ной на всю ширину В этой зоны, то задача упростится. В этом случае условие достаточной пластичности зоны разрушения А1кр > Al0 можно выразить следующим образом: разрушения при низком уровне напряжений не будет, если пластичность зоны разрушения

ь

а

МІМііі

У

Рис. 7.11 Схема задачи о перемеще­ниях их края полуплоскости от распределенной нагрузки qx

-Л верждение звучит весьма правдо­подобно.

>

V

X

достаточна для того, чтобы запол­нить раскрытие ожидаемой тре­щины под действием собственных напряжений. На мой взгляд, с фи­зической точки зрения такое ут-

Для приближенной оценки рас­крытия трещины под действием собственных напряжений можно воспользоваться задачей о дейст-

вии распределенной нагрузки на

край полуплоскости. Решение этой задачи (рис. 7.11) приведено в книге С. П. Тимошенко и Дж. Гудьера «Теория упругости».

Перемещение их края упругой полуплоскости в точке с коорди­натой у, от нагрузки qx(£), распределенной на промежутке a < £ < b, вычисляется по формуле

b a

Так как бесконечная полуплоскость даже от очень малой силы перемещается на бесконечное расстояние, формула (7.18) пригод­на только для вычисления разности перемещений двух точек с координатами у1 и у2. Одну из этих точек можно считать закреп­ленной.

7.3.4.1.

УПРУГАЯ ПОДАТЛИВОСТЬ ПОЛЕЙ СВАРОЧНЫХ НАПРЯЖЕНИЙ

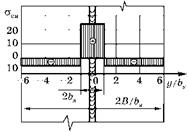
На рис. 7.12 приведена упрощенная эпюра продольных свароч­ных напряжений у продольного стыкового шва на пластине ши­риной B.

В пределах упругопластической зоны на ширине 2bs сварочные напряжения равны пределу текучести стт. Для стали ВСт3 предел текучести стт = 24 кг/мм2. Вне этой зоны сварочные напряжения определяются исходя из уравнения равновесия:

^ X = 0; ат • 2bs +асв • 2B = 0;

откуда:

(7.19)

где р = B/bs — относительная ширина пластины.

°св E ■ Ацт Е ■ 2 ■ B ■ t"

(7.20)

Рис. 7.12 Упрощенное распределение напряжений в пластине с продольным сварным швом

По теории сварочных напря­жений Н. О. Окерблома эти сва­рочные напряжения можно вы­числить, зная погонную энергию сварки:

Здесь Ацт — наблюдаемая деформа­ция укорочения свариваемой пла­стины; ц — коэффициент продоль­ного укорочения, для ВСт3 ц =

= -3,5310-6 см3/кал; qn — погон­ная энергия сварки:

кал/см,

0,24• 1св • ид - л

qn

св

р-1 2 • B • t

откуда

Р = B = 1 ------- bs ^Е •q.

= 1 --

^•Чп

где 0,24 — коэффициент пересчета ватт на калории; 1св — свароч­ный ток, A; ид — напряжение на дуге, V; л — к. п. д. дуги: для руч­ной дуговой сварки л = 0,75, для автоматической под слоем флю­са — 0,8; vсв — скорость сварки, см/с; B — ширина свариваемой пластины, см; t — толщина пластины, см. Приравнивая сварочные напряжения вдали от шва из формул (7.19) и (7.20), можно получить выражение для вычисления коэф­фициента р: 1 ^ V-Чп

2 B•t' 2 • єТ • B • t

(7.21)

= Е •

Обозначим в этом расчете ширину зоны разрушения через 2bc, а отношение этой ширины к ширине упругопластической зоны через Рс = bc/bs. Если ширина зоны разрушения bc меньше ширины упругопла­стической зоны bs, то из рис. 7.12 следует, что вся зона разрушения находится в поле равномерных сварочных напряжений растяже­ния, равных пределу текучести стт. В этом случае для определения упругой податливости поля сварочных напряжений нужно к кра­ям трещины длиной 2bc приложить давление, равное стт. Такая за­дача уже была рассмотрена в разделе 6.3.3 при выводе формулы Гриффитса для критических напряжений. Из формулы (6.76) сле­довало, что при нагрузке q = ст0 трещина длиной 2L превращается

в эллипс с полуосями L и а, где a = 2 • —0• L. E

Но в рассматриваемой задаче: ст0 = стт; стт/Е = sT; L = bc; Al0 = 2a. Поэтому при bc < bs или при Рс < 1 упругая податливость поля сва­рочных напряжений может вычисляться по формуле

Al) = 4 - єТ • bc. (7.22)

В обычных условиях зона разрушения, в которой идут пласти­ческие деформации, ограничивается пределами упруго пластиче­ской зоны у сварного шва. Однако если этот сварной шов находится в зонах конструктивной концентрации или действия реактивных напряжений, ширина зоны разрушения может быть больше. Тогда на всей ее ширине 2bc нужно интегрировать влияние нагрузки по формуле (7.18). Схема этой задачи показана на рис. 7.13а.

б

2 4 6 2 B/bs

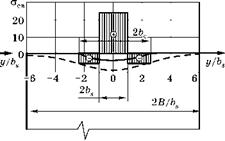
Рис. 7.13 Замена половины трещины полуплоскостью

а °СВ 20 10 0 -10

-V-

26.

-2 2 Ъ. Лг

Но аналитического решения задачи о перемещениях краев тре­щины при приложении к ее краям произвольной распределенной нагрузки нет. Поэтому приходится ее заменить задачей о переме­щениях краев полуплоскости под действием распределенной на­грузки, как показано на рис. 7.136. При этом вместо перемеще­ний краев трещины, показанных сплошной линией, получатся перемещения краев полуплоскости (пунктир). Чтобы эту пунктир­ную линию «выпрямить» при у < —bc и y > +bc, нужно в этих зонах приложить дополнительно распределенную нагрузку, направлен­ную вверх и резко возрастающую при приближении к точкам ±bc. Но отыскание закона распределения такой нагрузки — достаточ­но сложная задача. Поэтому ниже сделана попытка определить упругую податливость по формуле

Alo = 2 • (ux(0) - Mbc)), где перемещения ux(0) и ux(bc) вычисляются по формуле (7.18).

Согласно рис. 7.13 и формуле (7.19) нагрузка q(^) задана в виде: при ^2 < b2 q(£) = ст;

при ^2 < bf q(^) = _стт • р^.

В этом случае интеграл формулы (7.18) разбивается:

bs bc J ln(y -%)-d^ + Jln(y -%) d

йх (У) ^-^Ё 'Я • J ln(y-^)-d^+ir-/-

-b‘ или

2-£t P

йх (y) =--- ^ • jAb, У) + p-f! • [/ 2(bs, bc, y) + f 3(bs, bc, y)]j,

где f1, f2 и f3 — соответствующие определенные интегралы:

f1(bs, У) = (У + bs) • ln(|y + bs|) - (y - bs) • ln(|y - bs|) - 2 • bs; f2(bs, bc, y) = (y + bc) • ln(|y + bj) - (y + bs) • ln(|y + bs|) + bs - b^; f3(bs, b^ y) = (y - bs) • ln(|y - bs^ - (y - bc) • ln(|y - bc) + bs - bc.

Не зависящие от координаты y слагаемые в последних форму­лах на результаты вычисления податливости не влияют, так как уничтожаются при вычислении разности перемещений двух то­чек. Кроме того, для общности лучше перейти к безразмерным величинам. Поделив последние формулы на bs и обозначив y/bs = % и bc/bs = pc, получим:

F1( X) = f1(bbs, y) (X +1) • ln(| x +1|) - (X-1) • ln(| X-1|);

bs

F2(Pc, X) = f 2(bs, bc, y) = (X + Pc) • ln(| x + Pc |) - (x +1) • ln(| x + 1|);

s

F3(Pc

, X) = f 3(bs, bc, y) =(X-1) •ln(|X-1|)-(X-P) •lndX-PeD.

b

С учетом этих выражений безразмерное перемещение составит:

йх (P, Pc, X) = = - -^|f1(x) + P-P1 • [F2(pc, X) + F 3(pc, x)]

St • bs л | P-1

и формула для вычисления упругой податливости поля свароч­ных напряжений при bc > bs приобретает вид

= 2 • [йх(P, Pc,0) - йх(P, Pc, bc) +1]. (7.23)

ST • bs

		10
	5^
			Р =	100
	N

Рс

А1о bs-£T 10

Рис. 7.14

Влияние относительной ширины зоны разрушения рс = bc/bs на упругую податливость поля сварочных напряжений Al0 при разной относительной ширине пластины р = B/bs

Единица в последней формуле добавлена для учета поправки на искривленность кромки полуплоскости при У > bc для того, чтобы это выражение сопрягалось с формулой (7.22).

График зависимостей, вычисленных по формулам (7.22) и (7.23), показан на рис. 7.14.

Видно, что с увеличением относительной ширины зоны разру­шения bc в 10 раз упругая податливость возрастает с 2 до 5, т. е. в

2,5 раза. Относительная ширина пластины р = B/bs довольно сла­бо влияет на эту зависимость. С уменьшением р наклон кривой несколько возрастает.

Оценим абсолютную величину Al0 при ручной дуговой сварке.

Пусть сечение пластины равно: 2B = 2 • 100 см; t =1 см.

-3.

Сталь ВСт3, E = 2,1104 кг/мм2; стт = 24 кг/мм2; гТ = 1,1410 ц = -3,5310-6 см3/кал;

Ручная дуговая сварка. qп = 1500 кал/см.

По формуле (7.21) вычислим р:

Р B, 2-гТ B t, 2 1,14 10-3 100 1

Р = — = 1------ ----------- = 1--------------------------- = 44,16.

н bs ^^п -3,53 10-6 1500

Полуширина зоны упругопластических деформаций:

100

= 2,26 см.

b = B =

s Р 44,16

Упругая податливость поля сварочных напряжений при bc = bs: Al0 = 4 єг • bs = 4 • 1,14103 • 2,26 = 0,0103 см = 0,103 мм.

При автоматической сварке под флюсом погонная энергия мо­жет составлять qп = 5000 кал/см. Повторение приведенного выше расчета при этой погонной энергии дает Al0 = 0,33 мм.

Таким образом, одни сварочные напряжения у продольных швов дают упругую податливость порядка десятых долей мил­лиметра.

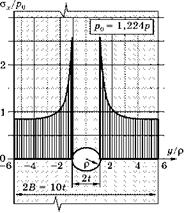
Рис. 7.15 Распределение напряже­ний ох = о1 по минималь­ному сечению растянутой вдоль оси x пластины с отверстием t/p = 1,1 шириной 2B = 101

1/2

Ы 1

Ф =

Но если на это поле наложить дополнительный фактор, такой чтобы зона пластических деформаций захватила сжатую при свар­ке часть пластины, то, как следует из рис. 7.14, упругая податли­вость может возрасти в 2,5 раза. Тогда при ручной дуговой сварке она составит 0,25 мм, а при автоматической — 0,82 мм. Это уже представляет опасность даже при вязком разрушении металла.